Основные понятия об отображении эллипсоида и сфер на плоскости

Связь картографии с другими науками.

Теория картографии опирается на философские науки. В картографии находят применение: общая теория отражения, теория моделирования, методы формальной логики.

Различные отрасли картографии используются для разработки теории проекции, матаматическо–картографического моделирования, обеспечения автоматизации картографических процессов. Картография связана с автоматикой, электроникой, приборостроением, химическими технологиями.

Картография связана с геодезией. От геодезии картография использует данные о фигуре, размерах Земли, о гравитации. Основой для картографирования служат топосъемки местности. Материалы аэро- и космической съемок используются для составления обновления и уточнения топографических и тематических карт. Имеются связи картографии с комплексом наук о Земле. Они проявляются в том, что картография служит основным средством познания географии, экологии, геологии, геофизики, океанологии и планетологии, имеются связи с социально-экономическими науками.

Для того, чтобы отобразить картографируемую поверхность на плоскости необходимо сначала от физической поверхности перейти к вспомогательной поверхности, которая наиболее близка к физической и может быть выражена математическими уравнениями, а затем к плоскости.

Для обеспечения непрерывности изображения при создании карт прибегают к картографическим проекциям.

Математические законы выражают функциональную связь между координатами точек картографируемой поверхности и плоскостью.

Картографической проекцией называется математический способ отображения поверхности эллипсоида на плоскость.

Положение точек на земной поверхности определяется географическими координатами (широта и долгота), в изображении на плоскости им соответствуют точки с прямоугольными координатами (X и Y).

Связь между координатами точек на карте и соответствующими точками эллипсоида на поверхности определяется уравнениями:

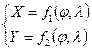(1.1)

При условии, что функции f_1, f₂ однозначны и непрерывны хотя бы для некоторых значений j и l.

Свойства проекций зависят от свойств и характера функций.

На сферической поверхности уравнения меридианной и параллелей имеют вид: 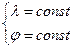(1.2)

На плоскости (в проекции) уравнение меридианов имеет вид 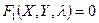, уравнение параллелей - 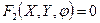(1.3)

Сетка меридианов и параллелей на земном эллипсоиде, шаре и на глобусе является координатной сеткой. Ее называют географической сеткой, а ее изображение на карте – картографической сеткой.

Наиболее простой вид сетки, если проекция описывается следующими уравнениями: 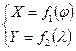. (1.4)

В этом случае параллели и меридианы прямые перпендикулярные линии.

Если сетка описывается следующими уравнениями: 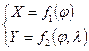, (1.5)

тогда параллели – прямые линии, а меридианы – кривые линии.

Если сетка описывается уравнениями: 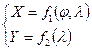, (1.6)

тогда параллели – кривые линии, а меридианы – прямые параллельные оси X.

Если уравнением (1.1), то параллели и меридианы – кривые.

Дата добавления: 2014-03-24; просмотров: 622; Нарушение авторских прав

Мы поможем в написании ваших работ!