
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Локальная теорема Муавра - Лапласа
Лекция 4. Повторные испытания. Локальная и интегральная теорема Муавра - Лапласа.
Наивероятнейшее число появления события А среди n повторных испытаний
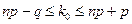
Пусть испытание проводилось 6 раз, в каждом из которых событие появлялось с вероятностью 0.4, тогда вероятность противоположного события равна q = 1 - p = 0.6 .
Следовательно, наивероятнейшее число появления событий 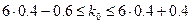
Формула Бернулли является точной, но она позволяет вычислить вероятность используя только маленькие факториалы, формулу Бернулли использовать трудоёмко , если количество испытаний велико, при этом существует множество теорем и формул с помощью которых можно вычислить P (k) приближённо, но с достаточной точностью.
(k) приближённо, но с достаточной точностью.
Теорема 4.1 пусть вероятность Р наступления события А в каждом повторном испытании постоянно равна р отлично от 0 и 1, то при достаточно больших n справедлива формула
P (k) =
(k) =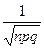
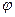 (x) , где x =
(x) , где x = 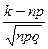 ;
; 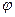 (x) =
(x) = 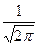 e
e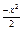
Замечание: формула Муавра - Лапласа является асимптотической формулой биноминального разложения, при достаточно больших n погрешность вычисления мала. Значение функции 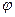 (х) имеется
(х) имеется в справочниках.
в справочниках.
Свойства функции:
1. Область определения: х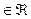 .
.
2. Область изменения 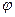 (х)
(х)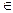 (0;
(0;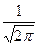 ].
].
3. Промежутки монотонности
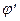 (х) =
(х) = 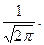 e
e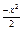
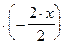 ;
; 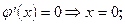
при x<0 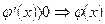 возрастает;
возрастает;
х>0 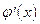 <0
<0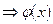 убывает.
убывает.
4. Промежутки выпуклости и вогнутости
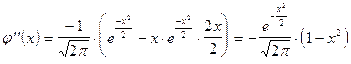
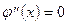
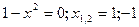
при 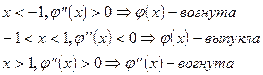
5. Асимптоты
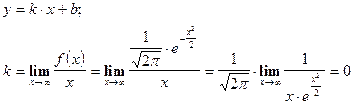
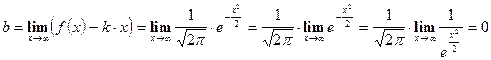
асимптоты горизонтальные 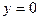

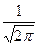



 |
-1 0 1 x
| <== предыдущая страница | | | следующая страница ==> |
| Повторные испытания. Формула Бернулли | | | Формула Пуассона |
Дата добавления: 2014-02-26; просмотров: 762; Нарушение авторских прав

Мы поможем в написании ваших работ!