
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Биномиальное распределение дискретной случайной величины. Распределение Пуассона
Пусть производится n независимых испытаний, в каждом из которых событие А может появляться либо нет. Вероятность появления события постоянна и равна р, вероятность непоявления события q=1-p. Рассмотрим в качестве дискретной случайной величины Х число появлений события А в этих испытаниях. Поставим задачу: найти закон распределения Х, т.е. определим возможные значения и их вероятности. Случайная величина А может принимать значения: 0,1,2,...,n. Вероятности найдем по формуле Бернулли:

Биномиальным называют распределение, определяемое по формуле Бернулли. Напишем биномиальный закон распределения в виде таблицы:
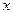
| n | n-1 | n-2 | . . . | |

| 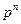
| 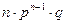
| 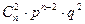
| . . . | 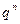
|
Для определения вероятностей появлений событий в испытаниях используют формулу Бернулли. Если n велико, то используют асимптотическую формулу Лапласа. Однако, если вероятность события мала, то прибегают к асимптотической формуле Пуассона. Найдем вероятность того, что в n испытаниях (при очень большом числе испытаний), в акждом из которых вероятность мала, событие наступает k раз. Предположим, nр сохраняет постоянное значение 1 (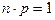 ), т.е. среднее число появления события в различных сериях испытаний остается неизменным.
), т.е. среднее число появления события в различных сериях испытаний остается неизменным.
Вывод формулы Пуассона:
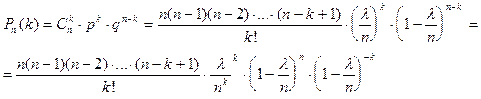
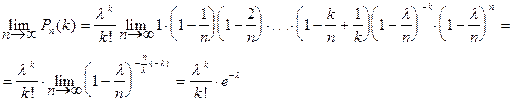
Закон распределения Пуассона определяет закон распределения вероятности массовых и редких испытаний.
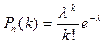 – затабулирована по
– затабулирована по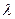 и
и 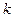 .
.
| <== предыдущая страница | | | следующая страница ==> |
| Статистика | | | Лекция 6. Числовые характеристики дискретных случайных величин |
Дата добавления: 2014-02-26; просмотров: 1102; Нарушение авторских прав

Мы поможем в написании ваших работ!