
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Важнейшие распределения
1.Случайная величина называется называется равномерно распределенной на (a,b) если ее плотность вероятности постоянна, a вне (a,b)=0.

Так как интеграл: 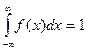 , то
, то 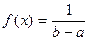 .
.
Мат. ожидание 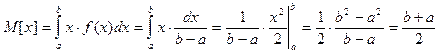
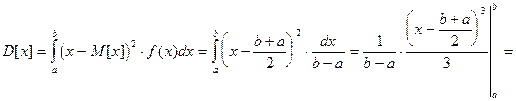
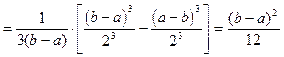
2.Случайная величина называется экспоненциально распределенной, если она имеет следующую плотность вероятности:
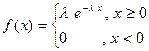
рис.2.
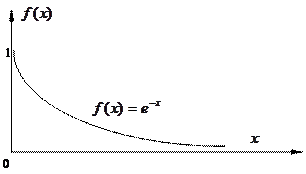
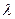 – параметр распределения.
– параметр распределения.
Пример. Длительность службы электрической лампы можно рассмотреть с хорошим приближением, как экспоненциально распределенную величину 
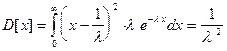
3.Среди случайных величин особенное, центральное место, занимают величины, плотность вероятности которых имеет вид: 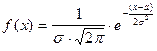 ,
,
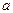 и
и 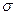 – параметры распределения. Такие случайные величины называются нормально распределенными.
– параметры распределения. Такие случайные величины называются нормально распределенными.
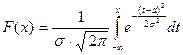 – нормальная функция распределения вероятностей. Употребляются наименования: гауссова случайная величина и рапределение вероятностей Гаусса.
– нормальная функция распределения вероятностей. Употребляются наименования: гауссова случайная величина и рапределение вероятностей Гаусса.
Таким образом нормальное распределение определяется двумя парами 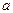 и
и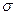 . Достаточно знать эти параметры, чтобы задать нормальное распределение. Можно показать, что для нормально распределенной случайной велличины
. Достаточно знать эти параметры, чтобы задать нормальное распределение. Можно показать, что для нормально распределенной случайной велличины 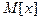 равно параметру
равно параметру 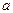 , т.е.
, т.е. 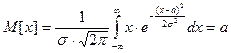
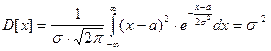
Среднеквадратичное отклонение нормального распределения равно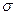 .
.
Замечание 1. Общим называется нормальное распределение с произвольными параметрами 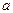 и
и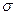 .
.
Нормированным называется нормальное распределение с параметрами 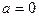 ,
, 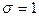 . Плотность нормированного распределения:
. Плотность нормированного распределения:
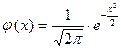 – эта функция табулирована.
– эта функция табулирована.
Замечание 2. 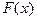 общего нормального распределения имеет вид (8.3.).
общего нормального распределения имеет вид (8.3.).
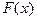 нормированного распределения:
нормированного распределения:
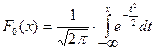 (8.3.)
(8.3.)
Можно проверить, что 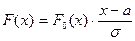 .
.
Замечание 3. Вероятность попадания нормированной случайной величины 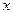 в
в 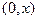 можно найти, пользуясь функцией Лапласа.
можно найти, пользуясь функцией Лапласа.
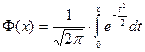 – интеграл вероятности.
– интеграл вероятности.
Замечание 4. Учитывая, что 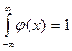 и следовательно в силу симметрии
и следовательно в силу симметрии 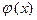 :
: 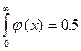 , т.е.
, т.е. 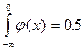 , то
, то 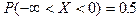 . Легко получить, что
. Легко получить, что 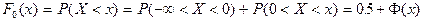
Укажем некоторые свойства 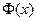 :
:
1. 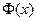 определена при всех значениях Х.
определена при всех значениях Х.
2. 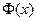 =0
=0
3. 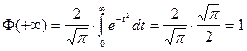
4. 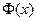 монотонно возрастает на
монотонно возрастает на 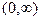 .
.
5. 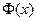 нечетна, так как
нечетна, так как 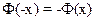 .
.
 |
| <== предыдущая страница | | | следующая страница ==> |
| Математическое ожидание и дисперсия непрерывных случайных величин | | | Нормальная кривая |
Дата добавления: 2014-02-26; просмотров: 805; Нарушение авторских прав

Мы поможем в написании ваших работ!