
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Зависимые и независимые лучайные величины
Теорема. Для того, чтобы случайные величины Х и Y были независимы, необходимо и достаточно, чтобы функция распределения 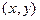 была равна произведению составляющих
была равна произведению составляющих
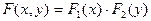 .
.
Следствие. Для того, чтобы случайные величины были независимы, необходимо и достаточно, что бы плотность совместного распределения системы была равна произведению плотности распределения составляющих
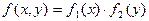 .
.
| <== предыдущая страница | | | следующая страница ==> |
| Условное математическое ожидание | | | Корреляционный момент. Коэффициент корреляции |
Дата добавления: 2014-02-26; просмотров: 619; Нарушение авторских прав

Мы поможем в написании ваших работ!