
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Нормальное распределение
Испытания с двумя возможными результатами: да или нет, удача или неудача, орлы или решки, красный или не красный и так далее, называют биномиальными испытаниями, а вероятность получения n1 «удач» в n биномиальных испытаниях определяется выражением
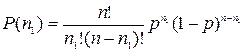 , (6.1)
, (6.1)
где р – вероятность «удачи» при одном испытании. Это формула биномиального распределения.
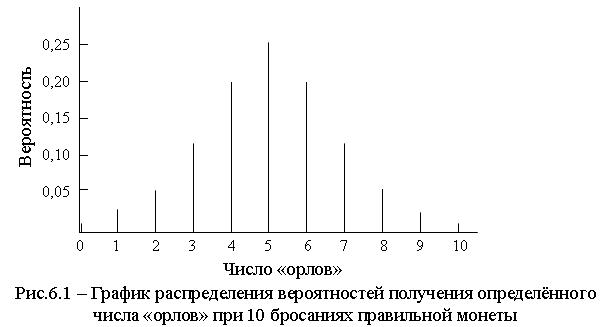
Предположим, что монета подбрасывается 10 раз. Допустим, что она может с равным успехом выпасть как «орлом», так и «решкой». Можно спросить, какова вероятность того, что в результате получится 0 «орлов» или что выпадет 1 «орёл»... или что в результате 10 бросаний мы получим 10 «орлов»? Вычисления, проведенные по формуле (6.1), позволили построить график распределения вероятностей получения определённого числа «орлов» при 10 бросаниях правильной монеты (рис. 6.1). Вероятности появления 0, 1, 2, ..., 9 или 10 «орлов» в результате 10 бросаний монеты графически представлены на рисунке 6.1.
Вероятности наблюдаемых значений непрерывных переменных, например роста, удобно изображать с помощью математических кривых, известных как распределения вероятностей.
Пусть известен рост для огромного числа разных людей, тогда можно построить график, где «рост человека» изображен в зависимости от доли людей, которые имеют этот рост.
Доля людей, рост которых лежит в пределах от 1,50 до 1,55 м, может рассматриваться как вероятность, что у человека, случайно выбранного из совокупности, рост будет в пределах от 1,50 до 1,55 м. Площадь под этой кривой равна 1.
Если изображать значения, которые может принимать непрерывная случайная переменная таким образом, что площадь между любыми двумя значениями переменной равна вероятности того, что переменная будет принимать значение, лежащее между этими двумя величинами, то результирующий график называют функцией плотности вероятности.
Если бы нам удалось найти уравнение кривой, которая бы хорошо аппроксимировала кривую, полученную соединением концов отрезков на рисунке 6.1. Если бы такую кривую удалось найти, то почти нереализуемые проблемы вычисления вероятностей (из-за громоздкости вычислений) можно было бы заменить простым считыванием точек с кривой или просмотром чисел в математической таблице
Уравнение такой кривой
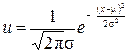 , (6.2)
, (6.2)
где u – высота кривой прямо над всяким заданным значением Х на графике распределения частот, величина 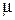 соответствует среднему распределения частот большой выборки, а
соответствует среднему распределения частот большой выборки, а 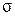 – стандартному отклонению этого распределения.
– стандартному отклонению этого распределения. 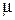 и
и 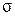 – числа, которые определяют положение кривой относительно числовой оси и регулируют её размах.
– числа, которые определяют положение кривой относительно числовой оси и регулируют её размах.
Уравнение (6.2) – формула для нормального распределения, график уравнения (6.2) – симметричная, колоколообразная кривая, известная как нормальная кривая.
Частным случаем нормальной кривой является единичная нормальная кривая. Для этой кривой 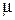 = 0,
= 0, 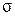 = 1, а площадь между кривой и осью абсцисс точно равна 1. Для обозначения нормально распределённой переменной с
= 1, а площадь между кривой и осью абсцисс точно равна 1. Для обозначения нормально распределённой переменной с 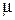 = 0 и
= 0 и 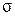 = 1 мы будем пользоваться буквой z. Самая высокая точка кривой расположена над нулевым значением z; в этой точке u
= 1 мы будем пользоваться буквой z. Самая высокая точка кривой расположена над нулевым значением z; в этой точке u 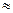 0,3989. Кривая симметрична относительно вертикали, проведённой через z =
0,3989. Кривая симметрична относительно вертикали, проведённой через z = 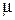 = 0 (нормальная кривая всегда симметрична относительно
= 0 (нормальная кривая всегда симметрична относительно 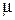 ), то есть асимметрия нормальной кривой равна нулю. Эксцесс нормальной кривой равен 3.
), то есть асимметрия нормальной кривой равна нулю. Эксцесс нормальной кривой равен 3.
Единичную нормальную кривую называют ещё стандартной. В таблицах даётся площадь под единичной нормальной кривой влево от любой точки на оси z между –3,00 и +3,00. Там приводятся также ординаты u единичного нормального распределения для значений z от –3,00 до +3,00. Например,
| Значение z | Площадь слева от z | Ордината для z |
| –1,27 0,00 0,50 1,96 | 0,1020 0,5000 0,6915 0,9750 | 0,1781 0,3989 0,3521 0,0584 |
площадь слева от z = –1,27 составляет 0,1020, а площадь слева от z = 0,50 равна 0,6915. Следовательно, площадь между –1,27 и 0,50 определяется разностью 0,6915 – 0,1020 = 0,5895. Иными словами, около 59% площади лежит между этими двумя точками.
На рисунке 6.2 построен график нормального распределения для 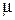 = 0 и
= 0 и 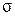 = 1.
= 1.

Рис. 6.2 – Нормальное распределение для 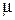 = 0 и
= 0 и 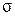 = 1
= 1
Фактически существует бесконечное множество нормальных кривых, отличающихся друг от друга парой значений 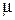 и
и 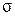 . Однако в любом нормальном распределении приблизительно:
. Однако в любом нормальном распределении приблизительно:
1. 68 % площади под кривой лежит в пределах одной 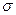 от среднего в любом направлении (то есть
от среднего в любом направлении (то есть 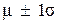 ).
).
2. 95 % площади под кривой лежит в пределах двух 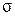 от среднего
от среднего 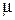 .
.
3. 99,7 % площади под кривой лежит в пределах трёх 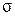 от среднего
от среднего 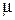 .
.
Если Х имеет нормальное распределение со средним 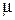 и стандартным отклонением
и стандартным отклонением 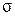 , то
, то 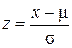 характеризуется нормальным распределением со средним 0 и стандартным отклонением 1, то есть
характеризуется нормальным распределением со средним 0 и стандартным отклонением 1, то есть 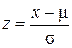 имеет единичное нормальное распределение. Площадь между х1 и х2 в нормальном распределении со средним
имеет единичное нормальное распределение. Площадь между х1 и х2 в нормальном распределении со средним 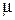 и стандартным отклонением
и стандартным отклонением 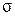 равна площади между
равна площади между 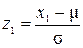 и
и 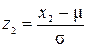 в единичном нормальном распределении.
в единичном нормальном распределении.
Величина 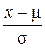 называется единичным нормальным отклонением. Если х имеет нормальное распределение со средним
называется единичным нормальным отклонением. Если х имеет нормальное распределение со средним 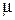 и стандартным отклонением
и стандартным отклонением 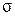 , то
, то 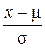 обладает единичным нормальным распределением.
обладает единичным нормальным распределением.
Если нам нужно узнать, какая часть площади лежит слева от значения 20 в нормальном распределении со средним 25 и стандартным отклонением 5, то для этого необходимо выяснить: «Какая часть площади лежит слева от 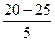 = –1 в единичном нормальном распределении?»
= –1 в единичном нормальном распределении?»
У многих учащихся иногда складывается неправильное представление, что существует необходимая связь между нормальным распределением – идеальным описанием некоторых распределений частот – и практически любыми данными. Нормальная кривая – это изобретение математика, довольно хорошо описывающее полигон частот измерений нескольких различных переменных. Никогда не была – да и не будет – получена совокупность данных, которые были бы точно нормально распределены. Но иногда полезно, допуская незначительную ошибку, утверждать, что значения переменной «нормально распределены».
Нормальное распределение играет важную роль как в описательной статистике, так и в теории статистического вывода.
Нормальная кривая является отличной аппроксимацией распределений частот большого числа наблюдений при множестве переменных. Полигоны частот роста взрослых мужчин и женщин подобны нормальной кривой.
Психометрические тесты общих и специальных умственных способностей часто дают распределения оценок, удовлетворительно согласующиеся с нормальным распределением. Довольно хорошо известно, что значения IQ интеллектуального теста Стенфорда – Бине распределены приблизительно нормально со средним ( 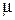 ) 100 и стандартным отклонением (
) 100 и стандартным отклонением ( 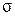 ) 16 для обычных людей (см. рис. 6.3). Тесты образовательной подготовки, строящиеся в соответствии с такими же психометрическими принципами, что и тесты способностей, обычно имеют полигоны частот, напоминающие нормальную кривую.
) 16 для обычных людей (см. рис. 6.3). Тесты образовательной подготовки, строящиеся в соответствии с такими же психометрическими принципами, что и тесты способностей, обычно имеют полигоны частот, напоминающие нормальную кривую.
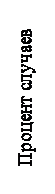
Рис. 6.3 – Распределение оценок IQ Стенфорда-Бине
| <== предыдущая страница | | | следующая страница ==> |
| | |
Дата добавления: 2014-11-01; просмотров: 649; Нарушение авторских прав

Мы поможем в написании ваших работ!