
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
К каноническому виду
|
Читайте также: |
Преобразование многомерных автоматических систем
Лекция 2
Каталоги и путь к файлу
Рассмотрим для примера структуру дискового пространства системы FAT, как самой простой.
Информационная структура дискового пространства - это внешнее представление дискового пространства, ориентированное на пользователя и определяемое такими элементами, как том (логический диск), каталог (папка, директория) и файл. Эти элементы используются при общении пользователя с операционной системой. Общение осуществляется с помощью команд, выполняющих операции доступа к файлам и каталогам.
Наиболее общей формой описания автоматической системы является нормальная (или стандартная) форма, например
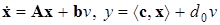 . (2.1)
. (2.1)
В развернутом векторно-матричном виде описание (2.1) выглядит следующим образом
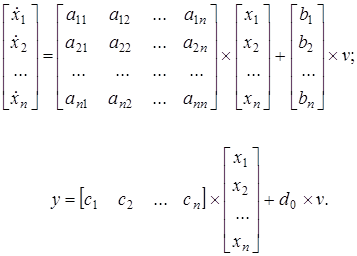
В скалярном виде описание автоматической системы (2.1) выглядит

Условия полной управляемости и полной наблюдаемости системы (2.1) следующие
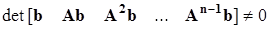 ,
,  .
.
Структура системы (структурная математическая модель) представлена на рисунке 2.1

Рисунок 2.1 – Структурная математическая модель системы (2.1)
В тех случаях, когда собственные числа 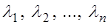 матрицы состояния
матрицы состояния  вещественные и различные, система (2.1) может быть преобразована к каноническому виду
вещественные и различные, система (2.1) может быть преобразована к каноническому виду
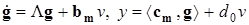 , (2.2)
, (2.2)
где  - диагональная матрица Жордана (Camille Jordan, 1838 - 1922).
- диагональная матрица Жордана (Camille Jordan, 1838 - 1922).
В развернутом векторно-матричном виде описание (2.2) выглядит следующим образом

В скалярном виде описание автоматической системы выглядит следующим образом

Если система (2.1) обладает свойством полной управляемости, то 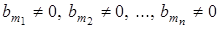 .
.
Если система (2.1) обладает свойством полной управляемости, то  .
.
Структура системы (2.2) представлена на рисунке 2.2.

Рисунок 2.2 – Структурная математическая модель системы (2.2)
2.1. Метод преобразования с помощью присоединенной матрицы. Преобразование системы вида (2.1), структура которой представлена на рисунке 2.1, к системе вида (2.2), структура которой представлена на рисунке 2.2, можно осуществить линейным преобразованием 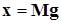 ,
,  , при этом
, при этом 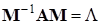 ,
, 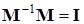 ,
, 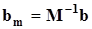 ,
,  , где матрица
, где матрица 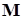 получается на основе
получается на основе 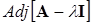 (присоединенной матрицы). При этом столбцы матрицы
(присоединенной матрицы). При этом столбцы матрицы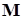 выбираются пропорционально произвольному столбцу матрицы
выбираются пропорционально произвольному столбцу матрицы  ,
, 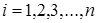 .
.
Пример 2.1.1. Рассмотрим систему (2.1) при 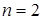 .
.
 . (2.3)
. (2.3)
В структурном виде система (2.3) представлена на рисунке 2.3.

Рисунок 2.3 – Структура системы (2.3)
Система обладает свойством полной управляемости, если
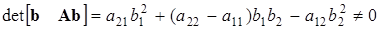 .
.
Система обладает свойством полной наблюдаемости, если
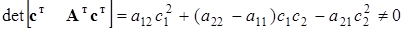 .
.
Линейным преобразованием 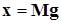 ,
,  приведем систему к виду
приведем систему к виду
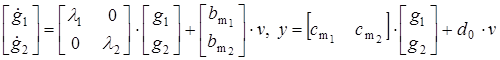 (2.4)
(2.4)
со структурой представленной на рисунке 2.4.
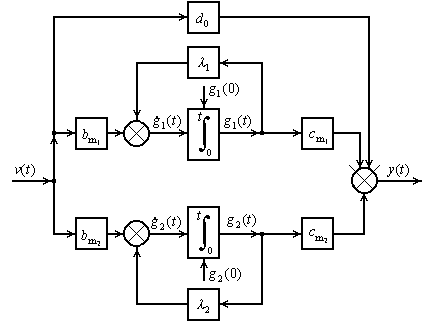
Рисунок 2.4 – Структура преобразованной системы (2.3) в общем виде
Матрица  ,
, 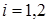 при: а)
при: а) 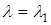 и б)
и б)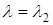 , где
, где 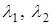 (при этом
(при этом 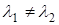 ) - собственные числа матрицы
) - собственные числа матрицы  , будет иметь соответственно вид:
, будет иметь соответственно вид:
а)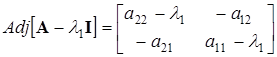 , б)
, б) . (2.4)
. (2.4)
Выбрав, например, первый столбец матрицы 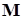 пропорционально первому столбцу матрицы (2.4-а), второй – пропорционально второму столбцу матрицы (2.4-б), получим матрицу канонического преобразования
пропорционально первому столбцу матрицы (2.4-а), второй – пропорционально второму столбцу матрицы (2.4-б), получим матрицу канонического преобразования
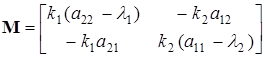 ,
,  , (2.5)
, (2.5)
где 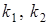 – любые вещественные числа (не нулевые).
– любые вещественные числа (не нулевые).
В преобразованном виде система (2.3) соответствует описанию (2.2) при 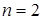 со структурой, представленной на рисунке 2.4. Элементы матриц
со структурой, представленной на рисунке 2.4. Элементы матриц  и
и 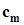 определяются в соответствии с преобразованием,
определяются в соответствии с преобразованием, 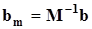 ,
, 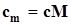 .
.
Допустим элементы матрицы состояния  имеют следующие числовые значения:
имеют следующие числовые значения: 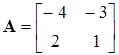 , тогда характеристический полином системы:
, тогда характеристический полином системы:
 .
.
Собственные числа матрицы состояния (корни характеристического полинома): 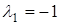 ,
, 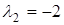 и соответственно
и соответственно
 ,
,
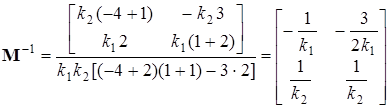 ,
,
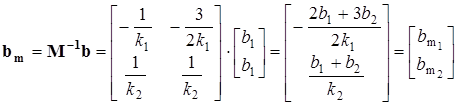 ,
,
 .
.
Если система обладает свойством полной управляемости, то 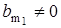 и
и 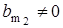 , или:
, или:
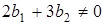 и
и  .
.
Если система обладает свойством полной наблюдаемости, то 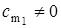 и
и 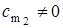 , или:
, или:
 и
и  .
.
Структура преобразованной системы (2.3) при 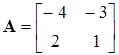 представлена на рисунке 2.5.
представлена на рисунке 2.5.
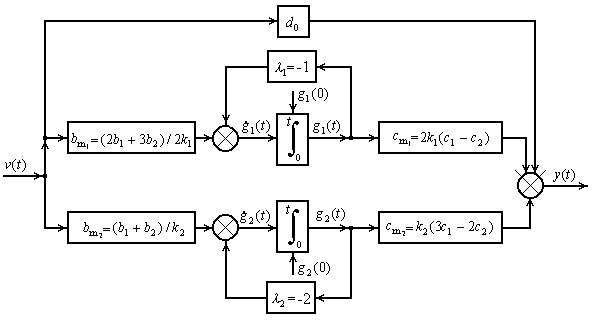
Рисунок 2.5 – Структура преобразованной системы (2.3) при 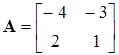 и
и  ,
, 
Пример 2.1.2.Допустим система (2.3) задана следующим описанием
 . (2.6)
. (2.6)
Структурный вид системы (2.6) представлен на рисунке 2.6.

Рисунок 2.6 – Структура системы (2.6)
Система не обладает свойством полной наблюдаемости:
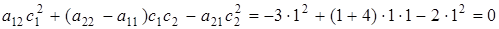
Система обладает свойством полной управляемости:
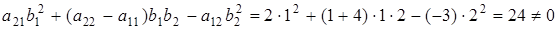
Преобразованием  ,
, 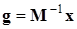 приведем систему к каноническому виду (2.4)
приведем систему к каноническому виду (2.4)
Собственные числа матрицы состояния: 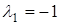 ,
, 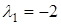 .
.
Матрицу канонического преобразования получим на основе  ,
, 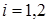 при
при  и
и  .
.
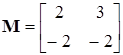 ,
, 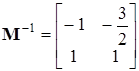 .
.
Элементы матриц  и
и 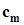 :
:
 ,
,  .
.
Каноническая форма исходной системы (развернутая векторно-матричная запись):
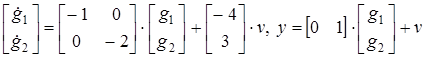 , где
, где
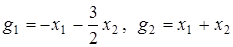 .
.
Структурный вид записи приведенной к канонической форме системы (2.6) представлен на рисунке 2.7.
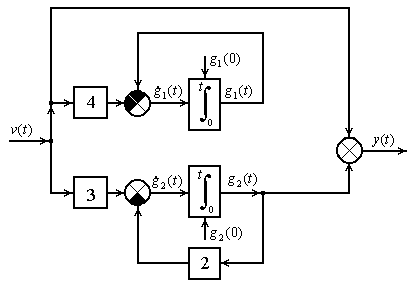
Рисунок 2.7 – Структура преобразованной системы (2.6)
Пример 2.1.3 Допустим система (2.3) задана следующим описанием
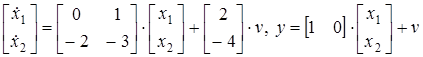 . (2.7)
. (2.7)
Скалярный вид записи системы:
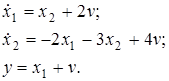
Структурный вид записи:
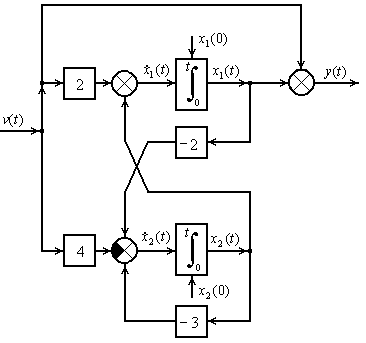
Рисунок 2.8 – Структура системы (2.7)
Система обладает свойством полной наблюдаемости. Система не обладает свойством полной управляемости:
 .
.
Преобразуем систему (2.7) с помощью матрицы 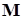 , полученной на основе
, полученной на основе 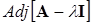 . При этом столбцы матрицы
. При этом столбцы матрицы 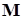 будут выбираться пропорционально произвольному столбцу матрицы
будут выбираться пропорционально произвольному столбцу матрицы  ,
, 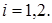
Характеристическое уравнение системы (2.7) 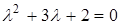 ;
;
Собственные числа матрицы  (корни характеристического уравнения)
(корни характеристического уравнения)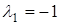 ,
, 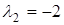 .
.
а) , б)
, б)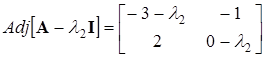 .
.
Выбрав, например, первый столбец матрицы 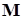 пропорционально первому столбцу матрицы (а), второй – пропорционально второму столбцу матрицы (б), где
пропорционально первому столбцу матрицы (а), второй – пропорционально второму столбцу матрицы (б), где 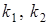 - коэффициенты пропорциональности. В результате получим матрицу канонического преобразования
- коэффициенты пропорциональности. В результате получим матрицу канонического преобразования
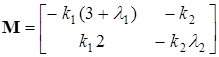 ,
,  .
.
С учетом того, что 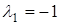 ,
, 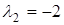 . получим
. получим
 ,
,  .
.
Выбрав  ,
, 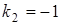 , получим матрицу канонического преобразования
, получим матрицу канонического преобразования
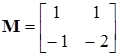 ,
, 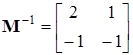 .
.
Элементы матриц  и
и 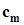 :
:
 ,
,  .
.
Каноническая форма исходной системы (развернутая векторно-матричная запись):
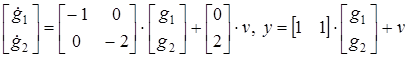 , где
, где
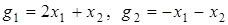 .
.
Структурный вид записи приведенной к канонической форме системы (2.7) представлен на рисунке 2.6.
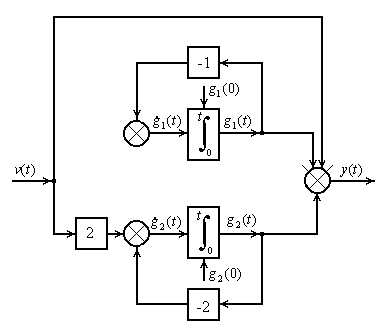
Рисунок 2.9 – Структура преобразованной системы (2.7)
| <== предыдущая страница | | | следующая страница ==> |
| NetWare File System | | | Потребность |
Дата добавления: 2014-02-27; просмотров: 637; Нарушение авторских прав

Мы поможем в написании ваших работ!