
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Дифференциальное исчисление функций многих переменных
Пусть 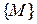 – множество точек пространства
– множество точек пространства  .
.
Если каждой точке 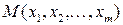 из множества
из множества 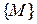 поставлено в соответствие по закону
поставлено в соответствие по закону 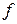 некоторое число
некоторое число  , то говорят, что на множестве
, то говорят, что на множестве 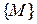 задана функция
задана функция 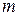 переменных
переменных 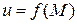 . Для функции
. Для функции 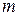 переменных используются также обозначения
переменных используются также обозначения  или
или  . Числовые переменные
. Числовые переменные 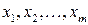 называются независимыми переменными или аргументами функции. Множество
называются независимыми переменными или аргументами функции. Множество 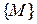 называется областью определения (или областью задания) функции
называется областью определения (или областью задания) функции 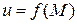 . Число
. Число 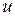 , соответствующее данной точке
, соответствующее данной точке 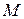 из множества
из множества 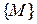 , называется значением функции в точке
, называется значением функции в точке 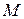 . Совокупность
. Совокупность  всех значений функции
всех значений функции 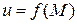 называется множеством значений этой функции.
называется множеством значений этой функции.
В евклидовом пространстве 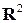 для функции
для функции 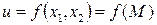 двух независимых переменных
двух независимых переменных  ,
,  обычно полагают
обычно полагают  ,
,  ,
,  , имея в виду, что точка
, имея в виду, что точка  лежит на координатной плоскости
лежит на координатной плоскости  прямоугольной декартовой системы координат
прямоугольной декартовой системы координат 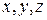 . Более того, если
. Более того, если  , то есть предположить, что значение
, то есть предположить, что значение  функции
функции 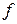 определяет аппликату
определяет аппликату  , то уравнение
, то уравнение 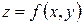 определяет поверхность в евклидовом пространстве
определяет поверхность в евклидовом пространстве 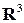 . Таков геометрический смысл функции двух независимых переменных. По тем же мотивам в пространстве
. Таков геометрический смысл функции двух независимых переменных. По тем же мотивам в пространстве 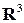 для функции трех независимых переменных вводят обозначение
для функции трех независимых переменных вводят обозначение  .
.
Если каждому натуральному числу 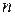 поставлена в соответствие точка
поставлена в соответствие точка  евклидова пространства
евклидова пространства  , то говорят, что в этом пространстве определена последовательность точек
, то говорят, что в этом пространстве определена последовательность точек 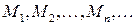 Эту последовательность обозначают также символом
Эту последовательность обозначают также символом  .
.
Последовательность  точек пространства
точек пространства  называется сходящейся, если существует точка
называется сходящейся, если существует точка 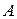 пространства
пространства  такая, что для любого положительного числа
такая, что для любого положительного числа  найдется номер
найдется номер 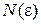 такой, что при
такой, что при  выполняется неравенство
выполняется неравенство 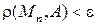 . При этом точка
. При этом точка 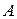 называется пределом последовательности
называется пределом последовательности  . Для предела
. Для предела 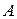 последовательности
последовательности  используются следующие обозначения:
используются следующие обозначения: или
или  при
при 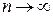 .
.
Существование предела последовательности  означает, что в любой
означает, что в любой  – окрестности точки
– окрестности точки 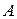 находятся все точки последовательности
находятся все точки последовательности  , начиная с некоторого номера
, начиная с некоторого номера 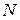 , зависящего, вообще говоря, от
, зависящего, вообще говоря, от  .
.
Последовательность  точек пространства
точек пространства 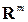 называется ограниченной, если существует такое число
называется ограниченной, если существует такое число 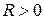 , что для всех
, что для всех 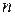 выполняется неравенство
выполняется неравенство 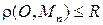 , где
, где 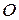 – точка, все координаты которой равны нулю. Ограниченность последовательности точек
– точка, все координаты которой равны нулю. Ограниченность последовательности точек 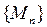 означает, что все точки этой последовательности содержатся в шаре радиуса
означает, что все точки этой последовательности содержатся в шаре радиуса  с центром в начале координат
с центром в начале координат 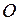 .
.
Число  называется пределом функции
называется пределом функции 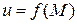 в точке
в точке 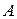 , если для любой сходящейся к
, если для любой сходящейся к 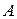 последовательности
последовательности  точек множества
точек множества 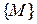 , все элементы
, все элементы  которой отличны от
которой отличны от 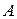 , соответствующая числовая последовательность значений функции
, соответствующая числовая последовательность значений функции 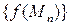 сходится к числу
сходится к числу  . Для обозначения предела функции
. Для обозначения предела функции 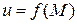 в точке
в точке 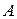 используются следующие обозначения:
используются следующие обозначения:
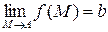 или
или 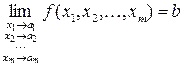 ,
,
где (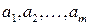 ) – координаты точки
) – координаты точки 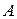 . Заметим, что в определении предела не рассматривается значение функция
. Заметим, что в определении предела не рассматривается значение функция 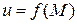 в точке
в точке 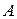 .
.
Функция 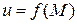 называется непрерывной в точке
называется непрерывной в точке 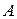 , если предел этой функции в точке
, если предел этой функции в точке 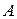 существует и равен значению
существует и равен значению  . Точки пространства
. Точки пространства 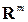 , в которых функция
, в которых функция 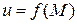 не обладает свойством непрерывности, называются точками разрыва этой функции. Функция
не обладает свойством непрерывности, называются точками разрыва этой функции. Функция 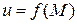 , определенная на множестве
, определенная на множестве 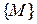 , называется непрерывной на множестве
, называется непрерывной на множестве 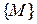 , если она непрерывна в каждой точке
, если она непрерывна в каждой точке 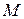 этого множества.
этого множества.
Приращением или полным приращением функции 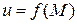 в точке
в точке 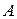 называется функция
называется функция  , определяемая равенством
, определяемая равенством
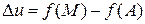 ,
,
где 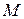 – произвольная точка из области определения функции.
– произвольная точка из области определения функции.
Пусть точки 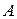 и
и 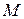 имеют соответственно координаты
имеют соответственно координаты 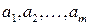 и
и 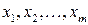 . Обозначая приращения аргументов
. Обозначая приращения аргументов 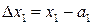 ,
,  ,…,
,…,  , получим для приращения функции
, получим для приращения функции  следующее выражение:
следующее выражение:
 .
.
Очевидно, для непрерывности функции 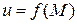 в точке
в точке 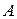 необходимо и достаточно, чтобы ее приращение
необходимо и достаточно, чтобы ее приращение  представляло собой бесконечно малую в точке
представляло собой бесконечно малую в точке 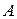 функцию, то есть
функцию, то есть
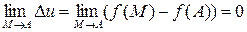 или
или 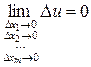 .
.
Зафиксируем все аргументы, кроме 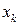 , и придадим
, и придадим 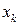 произвольное приращение
произвольное приращение  такое, чтобы точка с координатами
такое, чтобы точка с координатами  находилась в области определения функции.
находилась в области определения функции.
Частным приращением функции 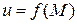 в точке
в точке 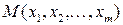 , соответствующим приращению
, соответствующим приращению  аргумента
аргумента 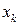 , называется функция
, называется функция  , определяемая равенством
, определяемая равенством
 .
.
Функция  называется непрерывной в точке
называется непрерывной в точке 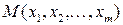 по переменной
по переменной  , если частное приращение
, если частное приращение  этой функции в точке
этой функции в точке 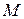 представляет собой бесконечно малую функцию от
представляет собой бесконечно малую функцию от  . Очевидно, из условия непрерывности функции
. Очевидно, из условия непрерывности функции  в точке
в точке 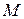 вытекает непрерывность этой функции в данной точке по каждой из переменных
вытекает непрерывность этой функции в данной точке по каждой из переменных 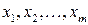 . Однако из непрерывности функции в точке
. Однако из непрерывности функции в точке 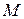 по каждой из переменных
по каждой из переменных 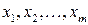 не вытекает, вообще говоря, непрерывность этой функции в точке.
не вытекает, вообще говоря, непрерывность этой функции в точке.
Зафиксируем все аргументы, кроме 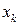 , и придадим
, и придадим 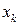 произвольное приращение
произвольное приращение  такое, чтобы точка с координатами
такое, чтобы точка с координатами  находилась в области определения функции.
находилась в области определения функции.
Частным приращением функции 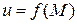 в точке
в точке 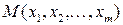 , соответствующим приращению
, соответствующим приращению  аргумента
аргумента 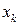 , называется функция
, называется функция  , определяемая равенством
, определяемая равенством
 .
.
Если существует предел
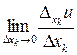 ,
,
то он называется частной производной функции  по переменной
по переменной 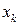 в точке
в точке 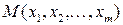 и обозначается любым из следующих символов:
и обозначается любым из следующих символов:
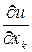 ,
,  ,
,  ,
,  .
.
Таким образом,
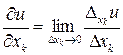 .
.
Отметим, что при фиксированных значениях всех аргументов, кроме 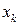 , функция
, функция  становится функцией одной переменной. Производная этой функции одной переменной и есть частная производная функции
становится функцией одной переменной. Производная этой функции одной переменной и есть частная производная функции  по аргументу
по аргументу 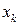 . Поэтому вычисление частных производных производится по тем же правилам, что и вычисление производных функций одной переменной.
. Поэтому вычисление частных производных производится по тем же правилам, что и вычисление производных функций одной переменной.
Функция  называется дифференцируемой в точке
называется дифференцируемой в точке 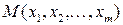 , если ее полное приращение в этой точке может быть представлено в виде
, если ее полное приращение в этой точке может быть представлено в виде
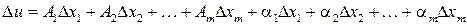 ,
,
где 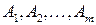 – некоторые не зависящие от
– некоторые не зависящие от 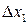 ,
, 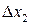 ,…,
,…, 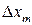 числа,
числа,  – бесконечно малые функции при
– бесконечно малые функции при 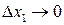 ,
,  ,…,
,…,  , равные нулю при
, равные нулю при  .
.
Дифференциалом  (полным или первым дифференциалом) дифференцируемой в точке
(полным или первым дифференциалом) дифференцируемой в точке 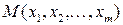 функции
функции  называется линейная относительно приращений аргументов часть приращения этой функции в точке
называется линейная относительно приращений аргументов часть приращения этой функции в точке 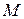 .
.
Таким образом, дифференциалом  дифференцируемой в точке
дифференцируемой в точке 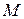 функции
функции  называется выражение
называется выражение
 .
.
Можно переписать выражение для полного дифференциала  следующим образом:
следующим образом:
 .
.
Дифференциалом независимой переменной  будем называть приращение этой переменной
будем называть приращение этой переменной 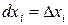 . Тогда эту формулу можно записать в виде
. Тогда эту формулу можно записать в виде
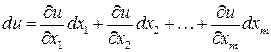 .
.
Пусть функция  имеет частную производную
имеет частную производную  в каждой точке некоторой окрестности точки
в каждой точке некоторой окрестности точки 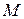 . В этом случае частная производная
. В этом случае частная производная  представляет собой функцию переменных
представляет собой функцию переменных 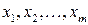 , определенную в данной окрестности.
, определенную в данной окрестности.
Если  имеет в точке
имеет в точке 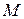 частную производную по аргументу
частную производную по аргументу  , то эта производная по аргументу
, то эта производная по аргументу 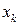 называется частной производной второго порядка или второй частной производной функции
называется частной производной второго порядка или второй частной производной функции  в точке
в точке 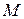 по аргументам
по аргументам  ,
, 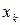 и обозначается одним из следующих символов:
и обозначается одним из следующих символов:
 ,
,  ,
, 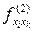 ,
, 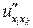 ,
, 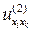 .
.
Если  , то частная производная второго порядка называется смешанной. Если
, то частная производная второго порядка называется смешанной. Если 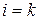 , то частная производная второго порядка обозначается
, то частная производная второго порядка обозначается 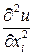 или
или 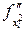 . После того как введено понятие второй частной производной, можно последовательно ввести понятие третьей частной производной, затем четвертой и так далее.
. После того как введено понятие второй частной производной, можно последовательно ввести понятие третьей частной производной, затем четвертой и так далее.
Пусть в некоторой области пространства  определена дифференцируемая функция
определена дифференцируемая функция  независимых переменных
независимых переменных 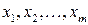 . Тогда в этой области дифференциал
. Тогда в этой области дифференциал  , определяемый выражением
, определяемый выражением
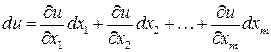 ,
,
так же можно рассматривать как функцию тех же независимых переменных. Если дифференциал  будет дифференцируемой функцией в соответствующей области пространства
будет дифференцируемой функцией в соответствующей области пространства  , то можно определить полный дифференциал
, то можно определить полный дифференциал  этой функции. Такой дифференциал обозначается символом
этой функции. Такой дифференциал обозначается символом 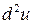 и называется вторым дифференциалом или дифференциалом второго порядка первоначальной функции
и называется вторым дифференциалом или дифференциалом второго порядка первоначальной функции  . Дифференциал
. Дифференциал 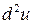 будет функцией тех же переменных, и если
будет функцией тех же переменных, и если 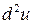 является дифференцируемой функцией в соответствующей области, то его полный дифференциал
является дифференцируемой функцией в соответствующей области, то его полный дифференциал 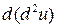 , обозначаемый символом
, обозначаемый символом 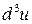 , приведет к третьему дифференциалу или дифференциалу третьего порядка первоначальной функции
, приведет к третьему дифференциалу или дифференциалу третьего порядка первоначальной функции 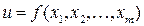 . Следуя индукции, нетрудно определить дифференциал
. Следуя индукции, нетрудно определить дифференциал 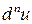 любого порядка
любого порядка 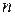 .
.
Пусть  – целое число, функция
– целое число, функция  задана в некоторой
задана в некоторой  - окрестности точки
- окрестности точки 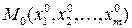 и имеет в этой окрестности непрерывные частные производные по всем переменным до порядка
и имеет в этой окрестности непрерывные частные производные по всем переменным до порядка  включительно. Тогда полное приращение
включительно. Тогда полное приращение  этой функции в точке
этой функции в точке  может быть представлено в форме
может быть представлено в форме
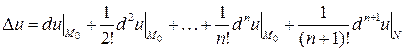 ,
,
при этом 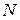 – некоторая точка указанной окрестности, зависящая, вообще говоря, от
– некоторая точка указанной окрестности, зависящая, вообще говоря, от 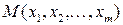 , а дифференциалы
, а дифференциалы  переменных
переменных  , входящие в выражения
, входящие в выражения 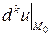 и
и  , равны
, равны 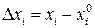 . Данный результат называется формулой Тейлора для функции
. Данный результат называется формулой Тейлора для функции 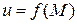 с центром разложения в точке
с центром разложения в точке  , а последний член формулы называется остаточным членом, записанным в форме Лагранжа.
, а последний член формулы называется остаточным членом, записанным в форме Лагранжа.
Пусть функция  определена в некоторой окрестности точки
определена в некоторой окрестности точки 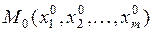 пространства
пространства 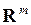 .
.
Говорят, что функция 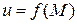 имеет в точке
имеет в точке 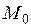 локальный максимум (локальный минимум), если существует такая окрестность точки
локальный максимум (локальный минимум), если существует такая окрестность точки 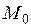 , в которой выполняется неравенство
, в которой выполняется неравенство 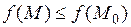 (
(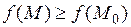 ). Если же существует окрестность точки
). Если же существует окрестность точки 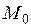 , в которой при
, в которой при 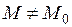 выполняются неравенства
выполняются неравенства 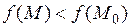 (
(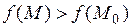 ), то говорят, что функция
), то говорят, что функция  имеет в точке
имеет в точке 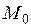 строгий локальный максимум (строгий локальный минимум). Если функция
строгий локальный максимум (строгий локальный минимум). Если функция  имеет в точке
имеет в точке 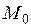 локальный максимум или локальный минимум, то говорят, что она имеет в этой точке локальный экстремум (или просто экстремум).
локальный максимум или локальный минимум, то говорят, что она имеет в этой точке локальный экстремум (или просто экстремум).
Необходимые условия локального экстремума. Если функция  имеет в точке
имеет в точке 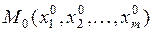 локальный экстремум, и в этой точке существуют частные производные первого порядка по всем переменным
локальный экстремум, и в этой точке существуют частные производные первого порядка по всем переменным  , то
, то
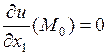 ,
, 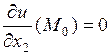 ,…,
,…, 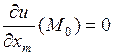 .
.
Точки, в которых обращаются в нуль все частные производные первого порядка функции  , называются стационарными точками этой функции.
, называются стационарными точками этой функции.
Квадратичная форма относительно переменных 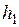 ,
, 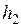 ,…,
,…, 

называется положительно определенной (отрицательно определенной), если для любых значений 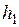 ,
, 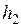 ,…,
,…,  , одновременно не равных нулю, эта форма принимает строго положительные (строго отрицательные) значения. Квадратичная форма называется знакоопределенной, если она является либо положительно определенной, либо отрицательно определенной. Квадратичная форма называется знакопеременной, если она принимает как строго положительные, так и строго отрицательные значения.
, одновременно не равных нулю, эта форма принимает строго положительные (строго отрицательные) значения. Квадратичная форма называется знакоопределенной, если она является либо положительно определенной, либо отрицательно определенной. Квадратичная форма называется знакопеременной, если она принимает как строго положительные, так и строго отрицательные значения.
Достаточные условия локального экстремума. Пусть функция 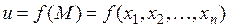 дифференцируема в некоторой окрестности
дифференцируема в некоторой окрестности  точки
точки 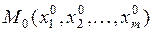 и имеет в этой точке непрерывные производные по всем переменным до второго порядка включительно. Кроме того, пусть точка
и имеет в этой точке непрерывные производные по всем переменным до второго порядка включительно. Кроме того, пусть точка 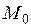 является стационарной точкой функции
является стационарной точкой функции 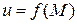 . Тогда если второй дифференциал
. Тогда если второй дифференциал
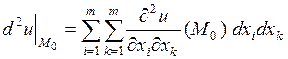 ,
,
представляет собой положительно определенную форму (отрицательно определенную) квадратичную форму от переменных 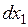 ,
,  ,…,
,…, 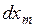 , то функция
, то функция  имеет в точке
имеет в точке 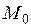 строгий локальный минимум (строгий локальный максимум). Если же второй дифференциал представляет собой знакопеременную квадратичную форму, то функция
строгий локальный минимум (строгий локальный максимум). Если же второй дифференциал представляет собой знакопеременную квадратичную форму, то функция 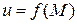 не имеет локального экстремума в точке
не имеет локального экстремума в точке  .
.
В предыдущей лекции рассмотрен вопрос отыскания локальных экстремумов функции, аргументы которой не связаны никакими дополнительными условиями, то есть являются независимыми переменными. Вместе с тем, в различных приложениях часто встречается задача об отыскании экстремумов функции, аргументы которой удовлетворяют дополнительным условиям связи. Экстремумы такого рода называют условными, чтобы отличить их от безусловных (или абсолютных) экстремумов, изученных ранее.
Функция 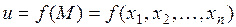 имеет условный максимум (условный минимум) в точке
имеет условный максимум (условный минимум) в точке 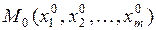 , если существует такая окрестность точки
, если существует такая окрестность точки 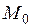 , что для всех точек
, что для всех точек 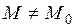 , удовлетворяющих уравнениям связи
, удовлетворяющих уравнениям связи
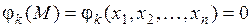 (
( ,
, 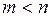 ),
),
выполняется неравенство 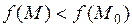 (соответственно
(соответственно  ).
).
Общий принцип нахождения условного экстремума заключается в следующем. Из уравнений связи выражаются одни переменные через другие, и после их подстановки в исходную функцию приходят к задаче на обычный (безусловный) экстремум, но уже для функции 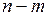 переменных. Данный метод использован в рассмотренном примере, однако, зачастую такой подход приводит к громоздким выкладкам, поэтому чаще используют другой метод – метод неопределенных множителей Лагранжа.
переменных. Данный метод использован в рассмотренном примере, однако, зачастую такой подход приводит к громоздким выкладкам, поэтому чаще используют другой метод – метод неопределенных множителей Лагранжа.
Рассмотрим метод неопределенных множителей Лагранжа для нахождения условного экстремума. Задача нахождения условного экстремума сводится к исследованию на обычный экстремум функции Лагранжа
 ,
,
где числа 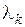 (
( ) – называются множителями Лагранжа.
) – называются множителями Лагранжа.
Необходимые условия условного экстремума выражаются системой  уравнений
уравнений
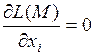 ,
, 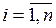 ,
,  ,
,  ,
,
из которой могут быть найдены неизвестные
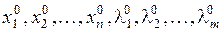 ,
,
где  – координаты точки, в которой возможен условный экстремум.
– координаты точки, в которой возможен условный экстремум.
Рассмотрим теперь достаточные условия условного экстремума функции нескольких переменных. Предположим, что в точке 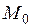 выполнены необходимые условия экстремума. Кроме того, дополнительно потребуем непрерывности всех частных производных второго порядка функций
выполнены необходимые условия экстремума. Кроме того, дополнительно потребуем непрерывности всех частных производных второго порядка функций 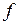 и
и 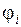 ,
, 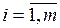 в окрестности точки
в окрестности точки 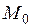 . Как было показано, для формулировки достаточного условия экстремума в точке
. Как было показано, для формулировки достаточного условия экстремума в точке 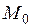 у функции
у функции 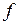 при наличии связей
при наличии связей 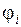 ,
, 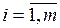 следует присоединить к необходимым условиям требование знакоопределенности
следует присоединить к необходимым условиям требование знакоопределенности 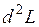 в этой точке. При этом можно утверждать наличие в точке
в этой точке. При этом можно утверждать наличие в точке 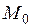 минимума, если
минимума, если  , и максимума, если
, и максимума, если  .
.
Дифференцируемая функция в ограниченной замкнутой области  достигает своего наибольшего (наименьшего) значения либо в стационарной точке, лежащей внутри области
достигает своего наибольшего (наименьшего) значения либо в стационарной точке, лежащей внутри области  , либо на границе этой области. Покажем на примере способ нахождения наибольшего и наименьшего значения функции двух переменных в замкнутой ограниченной области.
, либо на границе этой области. Покажем на примере способ нахождения наибольшего и наименьшего значения функции двух переменных в замкнутой ограниченной области.
Пусть требуется найти наибольшее и наименьшее значение функции 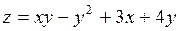 в замкнутой области
в замкнутой области  , ограниченной линиями
, ограниченной линиями  ,
, 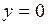 ,
,  .
.
Выясним сначала, существуют ли стационарные точки, лежащие внутри области  , то есть внутри треугольника
, то есть внутри треугольника 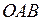 , где
, где 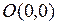 ,
, 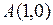 ,
,  . Имеем
. Имеем
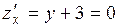 ,
,  .
.
Решая полученную систему уравнений, находим стационарную точку  . Она лежит вне области
. Она лежит вне области  , следовательно, при решении задачи ее не учитываем. Исследуем значения функции на границе области
, следовательно, при решении задачи ее не учитываем. Исследуем значения функции на границе области  .
.
На стороне  (
(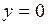 ,
,  ) треугольника
) треугольника 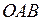 функция
функция 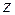 имеет вид
имеет вид  . Стационарных точек на отрезке
. Стационарных точек на отрезке  нет, так как
нет, так как  . В точках
. В точках 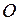 и
и  соответственно
соответственно 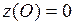 ,
, 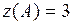 .
.
На стороне 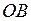 (
( ,
, 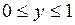 ) треугольника
) треугольника 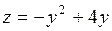 ,
, 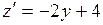 . Стационарную точку находим из уравнения
. Стационарную точку находим из уравнения  . Отсюда
. Отсюда  . Полученная точка с координатами
. Полученная точка с координатами 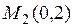 не принадлежит области
не принадлежит области  , поэтому исключается ее из рассмотрения. В точке
, поэтому исключается ее из рассмотрения. В точке  значение функции
значение функции 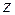 равно
равно  .
.
Находим наибольшее и наименьшее значения на стороне 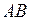 :
:  ,
,  . Здесь
. Здесь  ,
,  , тогда
, тогда  и из
и из 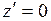 следует
следует  , то есть стационарная точка
, то есть стационарная точка  принадлежит границе области
принадлежит границе области  . Значение функции в ней
. Значение функции в ней 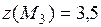 . Сравнивая все полученные значения функции:
. Сравнивая все полученные значения функции: 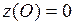 ,
, 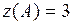 ,
, 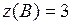 ,
, 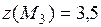 , видим, что
, видим, что 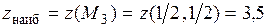 ,
, 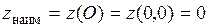 .
.
| <== предыдущая страница | | | следующая страница ==> |
| Виды правоотношений. Нужно различать понятия "объект права" и "объект правоотношения" | | | Ряды.Интегральное исчисление функций многих переменных и элементы векторного анализа |
Дата добавления: 2014-02-26; просмотров: 2086; Нарушение авторских прав

Мы поможем в написании ваших работ!