Студопедия

Главная страница Случайная лекция


Мы поможем в написании ваших работ!

Порталы:

БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика



Мы поможем в написании ваших работ!




Промежутки монотонности функции

Читайте также:
  1. Бесконечно малые и бесконечно большие функции.
  2. Вектор функции 2-х скалярных аргументов. Предел. Дифференцирование. Понятие поверхности. Гладкие поверхности и их параметризация с помощью вектор функции.
  3. Высшие психические функции.
  4. Гемоглобин. Его разновидности и функции.
  5. Деньги и их функции.
  6. Деньги, их свойства и функции. Уравнение обмена
  7. Дифференциал функции.
  8. Лекция № 13 Основные элементарные функции: постоянная, степенная, показательная, логарифмическая, тригонометрические, обратные тригонометрические функции.
  9. Лекция № 16 Предел функции в точке и на бесконечности. Основные теоремы о пределе функции. Односторонние пределы. Непрерывность функции. Первый и второй замечательные пределы.
  10. Маркетинг: понятие, цели, концепции, принципы и функции.

Определение 3. Функция 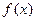называется возрастающей (убывающей) в промежутке 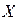из области определения, если для любых 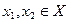из условия 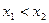следует неравенство 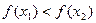(соответственно ).

На рисунке 2а функция возрастает в интервалах (a, b), (c, d), убывает в (b, c ).

Под монотонностью понимается либо возрастание, либо убывание.

Теорема 3 (достаточное условие монотонности). Если функция f(x) дифференцируема в промежутке 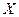и f ¢(x)>0 ( f ¢(x)<0 ) для всех 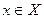, то f(x) возрастает (соответственно убывает) в промежутке X.

 

<== предыдущая страница | следующая страница ==>
Теорема Коши. Пусть функция f: [a, b] → R непрерывна на сегменте [a, b], и имеет конечную или бесконечную производную внутри этого сегмента | Экстремумы функции

Дата добавления: 2014-02-28; просмотров: 511; Нарушение авторских прав



Мы поможем в написании ваших работ!
lektsiopedia.org - Лекциопедия - 2013 год. | Страница сгенерирована за: 0.006 сек.