Ряды.Интегральное исчисление функций многих переменных и элементы векторного анализа

Числовым рядом (или просто рядом) называется выражение вида

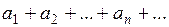, (1)

где 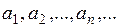– числовая последовательность. Для ряда также используется обозначения 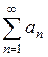. Числа 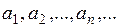называются членами ряда. Ряд (1) считается заданным, если известен его общий член 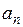, то есть известно правило 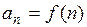, по которому каждому номеру (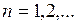) ставится в соответствие вполне определенный член ряда. Индекс принимает все целые значения от 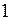до 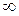. В некоторых случаях удобнее начинать нумерацию членов ряда не с 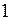, а с другого целого числа.

Сумма

,

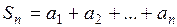слагаемыми которой являются первые членов ряда (1), называется -ой частичной суммой ряда (1), а ряд

,

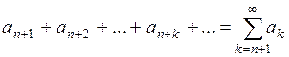членами которого являются все члены ряда (1), начиная с 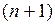-го, написанные в том же порядке, что и в ряде (1), называется -ым остатком ряда (1).

Ряд (1) называется сходящимся, если последовательность его частичных сумм 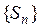сходится. Если ряд не сходится, то говорят, что он расходится.

Если ряд сходится, то предел

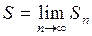
называется его суммой. В этом случае пишут

.

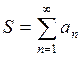Если 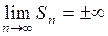, то соответственно пишут .

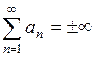Рассмотрим основные свойства сходящихся рядов.

1. Если сходится ряд (1), то сходится и любой из его остатков. Верно и обратное утверждение, из сходимости остатка вытекает сходимость исходного ряда.

Таким образом, отбрасывание конечного числа начальных членов или присоединение в начале его нескольких новых членов не отражается на сходимости ряда.

2.Если ряд (1) сходится, то сумма его -го остатка стремиться к нулю при .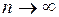

3. Если члены сходящегося ряда (1) умножить на один и тот же множитель 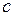, то сходимость ряда не нарушится, а сумма 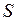умножится на .

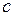4. Если ряды 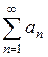и 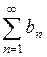сходятся, то ряды 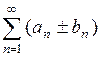также будут сходиться, а их сумма

.

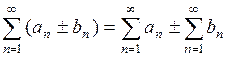Обратное утверждение неверно, то есть из сходимости ряда 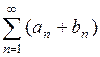или 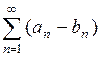не следует сходимость рядов 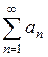и .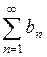

Замечание. Если ряд 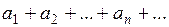сходится, то члены его можно любым образом сгруппировать скобками (не переставляя), например,

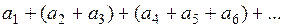
образуя новый ряд, члены которого равны суммам чисел стоящих в скобках. Новый ряд будет сходиться и притом к той же сумме. Обратное неверно, то есть раскрывать скобки в ряду, вообще говоря, незаконно, например, если убрать скобки в ряду 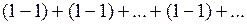, то получим расходящийся ряд.

5. (необходимый признак сходимости) Общий член 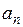сходящегося ряда стремится к нулю при .

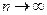Однако, условие 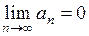не является достаточным, то есть при его выполнении ряд 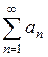может и расходиться.

Теорема (критерий Коши для ряда). Для того чтобы ряд 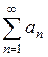сходился, необходимо и достаточно, чтобы для любого положительного числа 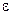нашелся номер 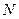такой, что для всех номеров 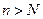неравенство

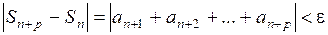
выполнялось при любом натуральном .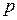

Изучим сходимость рядов все члены которых действительные положительные числа, такие ряды называются знакоположительными.

Теорема (интегральный признак сходимости рядов). Если функция 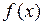, определенная при всех 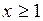положительна и монотонно убывает, то ряд 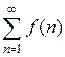сходится тогда и только тогда, когда сходится интеграл .

Теорема (признаки сравнения рядов). Пусть даны два ряда с положительными членами

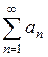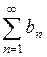(А) и (В).

(а) Если 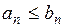(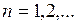), то из сходимости ряда (В) следует сходимость ряда (А); а из расходимости ряда (А) следует расходимость ряда (В).

(б) Если

,

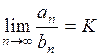то из сходимости ряда (В) при 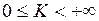следует сходимость ряда (А); а из расходимости ряда (А) при 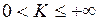следует расходимость ряда (В) (иначе, при 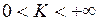оба ряда сходятся или расходятся одновременно).

Замечание. Признак, сформулированный в пункте (б) теоремы, называется предельным признаком сравнения рядов.

Теорема (признак Даламбера). Если члены знакоположительного ряда 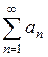таковы, что существует предел

,

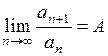то при 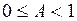данный ряд сходится, при 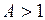– расходится, а при 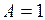– данный признак не может установить сходимость ряда.

Теорема (признак Коши). Пусть 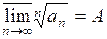. Тогда знакоположительный ряд 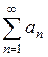сходится при 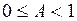, расходится 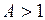при , при 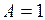установить сходимость ряда с помощью данного признака нельзя.

Ряд, члены которого могут быть как положительными, так и отрицательными числами называется знакопеременным.

Если ряд 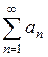сходится одновременно с рядом 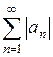, то ряд 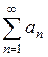называется абсолютно сходящимся.

Если ряд 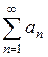сходится, а ряд 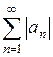расходится, то в этом случае ряд 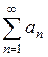называется условно сходящимся.

Замечание. Отметим, что в признаках Коши и Даламбера из расходимости ряда из модулей следует расходимость исходного ряда.

Ряд называется знакочередующимся, если его члены имеют поочередно, то положительный, то отрицательный знаки:

,

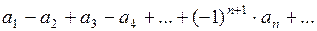где : .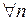

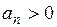Теорема (признак Лейбница). Если члены знакочередующегося ряда монотонно убывают по абсолютной величине:

: ,

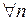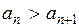и стремятся к нулю

,

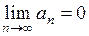то этот ряд сходится.

Рассмотрим последовательности и ряды, членами которых являются некоторые заданные функции, определенные на некотором числовом множестве .

Последовательность вида

,

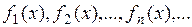элементами которой являются функции одной и той же переменной 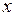, и определенные в некоторой области , называется функциональной последовательностью.

Ряд, составленный из элементов функциональной последовательности 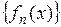называется функциональным рядом и обозначается

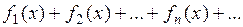или .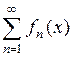

Если в точке 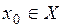сходится числовая последовательность 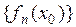, то говорят, что функциональная последовательность 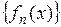сходится в точке 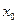. Множество всех точек сходимости последовательности 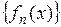называется областью сходимости функциональной последовательности .

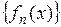Пусть для каждого 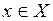последовательность 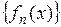сходится, то есть имеет конечный предел, который в общем случае зависит от выбора 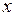и представляет собой функцию от 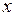на множестве :

.

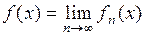Функцию 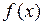называют предельной функцией для функциональной последовательности .

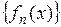Ряд 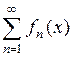называется сходящимся в точке 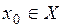, если сходится числовой ряд 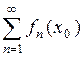. Множество точек сходимости ряда 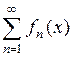называется областью сходимости этого функционального ряда. Очевидно, что сумма ряда 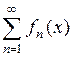в общем случае будет являться функцией переменной 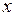, а именно, предельной функцией для функциональной последовательности частичных сумм данного ряда.

Свойства конечных сумм не всегда выполняются для числовых рядов. Также и свойства функций, из которых составлены функциональные последовательности или функциональные ряды, не всегда передаются предельной функции или, соответственно, сумме ряда. Рассмотрим пример, показывающий такой случай.

Пример. Исследовать на сходимость функциональную последовательность

, .

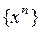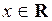∆ Очевидно, в зависимости от значения 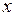предел последовательности 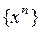принимает различные значения. Из свойств показательной функции следует, что

1) при ;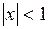

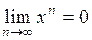2) при ;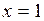

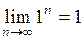3) при 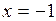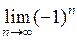– не существует;

4) при ;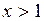

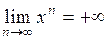5) при 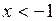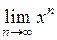; – не существует.

Следовательно, предельная функция последовательности 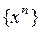имеет вид

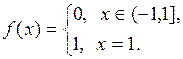
Таким образом, предельная функция 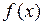определена не для всех 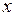в отличие от членов 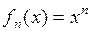функциональной последовательности 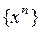которые определены для любого действительного 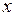. Кроме того, функции 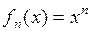непрерывны при любом 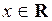, а предельная функция 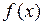разрывна в точке 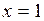(устранимый разрыв). ▲

Таким образом, для сохранения предельной функцией свойств функций, из которых составлена данная последовательность, необходимо наложить ограничения на характер сходимости. Такие ограничения приводят к понятию равномерной сходимости последовательностей (или рядов).

Допустим, что для всех 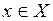существует предел 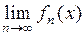, в этом случае говорят, что последовательность 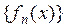сходится на множестве . Сформулируем это понятие по-другому, используя определение предела.

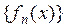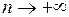Говорят, что последовательность при сходится на множестве к функции 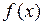, если для всех 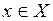и для любого положительного числа 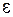найдется такой номер 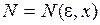, что для любого 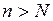будет справедливо неравенство .

Говорят, что последовательность 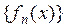при 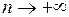сходится равномерно на множестве к функции 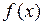, если для любого положительного числа 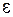найдется такой номер 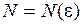, что для любого 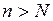и для всех 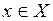будет справедливо неравенство .

Функциональный ряд 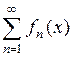, члены которого являются функции определенные на множестве , называется равномерно сходящимся на этом множестве, если последовательность его частичных сумм равномерно сходится на множестве .

Теорема (признак Вейерштрасса). Если члены функционального ряда 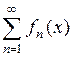удовлетворяют в области неравенствам

(),

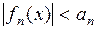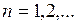где 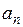– члены некоторого сходящегося числового ряда 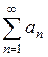, то ряд 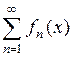сходится равномерно на .

Рассмотрим основные свойства равномерно сходящихся рядов.

Пусть задан функциональный ряд 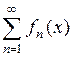, где 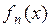определены в некоторой области .

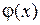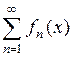1. Пусть функция ограничена на множестве , тогда если ряд равномерно сходится на множестве , то функциональный ряд 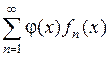также равномерно сходится на .

2. Если функции 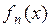непрерывны на множестве и ряд 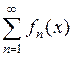равномерно сходится на , то тогда его сумма непрерывна на данном множестве и

, .

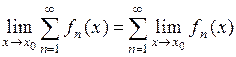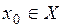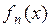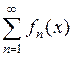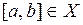3. Пусть функции непрерывны на множестве и ряд равномерно сходится на , тогда, если , то

.

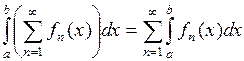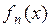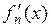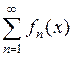4. Пусть функции имеют на непрерывные производные . Если на ряд сходится, а ряд 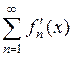сходится равномерно на , то в этом случае сумма ряда 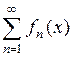имеет на производную, причем

.

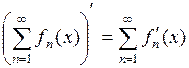Функциональные ряды вида

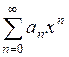, (2)

называются степенными рядами (коэффициенты 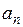не зависят от ).

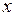Заметим, что также рассматриваются и более общая форма представления для степенных рядов 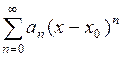. Однако заменяя 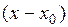на новую переменную, приходим к ряду (2).

Будем изучать вопрос об определении области абсолютной и равномерной сходимости, установим основные свойства таких рядов и возможность представления функций через степенные ряды.

Теорема 1 (Абеля). Если степенной ряд (2) сходится при 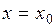, то он сходится и при том абсолютно при любом 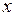, у которого .

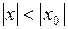Следствие. Если степенной ряд (2) расходится при 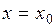, то он расходится и при всяком 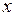, у которого .

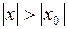Величина 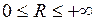такая, что при всех 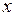, у которых 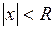, ряд (2) сходится, а при всех 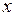, у которого 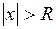, ряд (2) расходится, называется радиусом сходимости степенного ряда (2). А множество точек 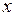, у которых 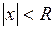, называется интервалом сходимости степенного ряда (2).

Из теоремы Абеля и признака Вейерштрасса следует справедливость следующей теоремы.

Теорема 2. У всякого степенного ряда (2) существует радиус сходимости 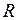. В интервале сходимости ряд (2) сходится абсолютно, а на любом отрезк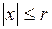е , где 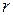фиксировано и 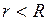, ряд (2) сходится равномерно.

Заметим, что для степенных рядов вида 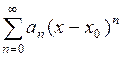интервал сходимости будет .

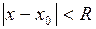Используя признаки Даламбера или Коши можно записать формулы для определения радиуса сходимости степенных рядов:

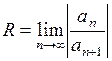или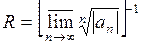

На основе теорем 1 и 2 и свойств равномерно сходящихся функциональных рядов можно сформулировать свойства сумм степенных рядов. Пусть задан ряд (2) имеющий радиус сходимости 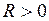, тогда для него будут справедливы следующие свойства.

1. Сумма 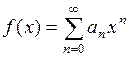степенного ряда (2) внутри его интервала сходимости представляет собой непрерывную функцию от .

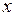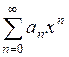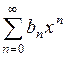2. Если два степенных ряда и в окрестности точки 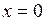имеют одну и ту же сумму, то эти ряды тождественны, то есть при любом выполняется .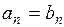

3. Сумма 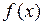степенного ряда (2) на интервале сходимости дифференцируема, и ее производная 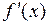может быть найдена почленным дифференцированием ряда (2), то есть

.

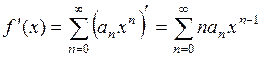Аналогично могут быть вычислены производные любого порядка функции .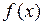

4. Сумма 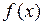степенного ряда (2) на интервале сходимости интегрируема и интеграл от нее может быть вычислен почленным интегрированием ряда (2), то есть, если 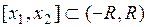, то

.

5. Степенные ряды, получающиеся из ряда (2) в результате почленного дифференцирования или интегрирования, имеют тот же радиус сходимости, что и ряд (2).

Замечание. Все перечисленные свойства справедливы и для степенного ряда 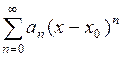с интервалом сходимости .

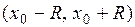Пусть функция 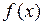является суммой степенного ряда 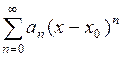, интервал сходимости которого 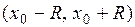. В этом случае говорят, что на интервале 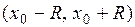функция 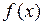разлагается в степенной ряд (или в ряд по степеням ).

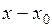Теорема. Если функция 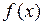на интервале 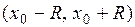разлагается в степенной ряд 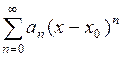, то

, ,

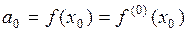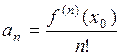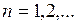
или

.

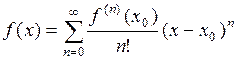Пусть 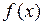определена в некоторой окрестности точки 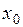и имеет в этой окрестности производные всех порядков.

Ряд вида

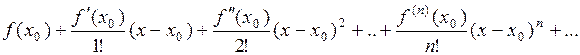(3)

называется рядом Тейлора функции 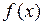в точке .

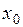При 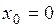ряд (3) называется рядом Маклорена.

Установим, при каких условиях сумма ряда (3) совпадает с функцией .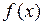

В курсе математического анализа была получена формула Тейлора для 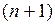- раз дифференцируемой в окрестности точки 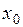функции

,

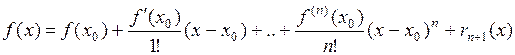где 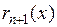– остаточный член формулы Тейлора, который можно записать в виде

, .

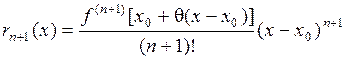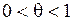Это остаточный член в форме Лагранжа.

Если обозначить 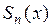– частичную сумму ряда Тейлора (3), то формулу Тейлора можно записать в виде

.

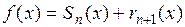Теорема. Для того чтобы ряд Тейлора (3) сходился на интервале 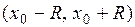и имел своей суммой функцию 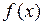, необходимо и достаточно, чтобы на этом интервале остаточный член 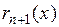формулы Тейлора стремился к нулю при .

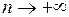Приведем еще одно достаточное условие разложимости функции в степенной ряд.

Теорема. Пусть функция 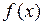и все ее производные ограничены в совокупности на интервале 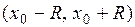, то есть найдется такое положительное число 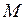, что для любого 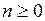и для любого 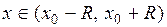будет справедливо неравенство 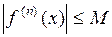. Тогда на интервале 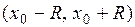функция 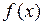раскладывается в ряд Тейлора (3).

Дата добавления: 2014-02-26; просмотров: 1829; Нарушение авторских прав

Мы поможем в написании ваших работ!