Обозначения

Будем обозначать элементы множества N большими буквами латинского алфавита. Элементы множества T – малыми латинскими буквами. Цепочки из V* - греческими буквами. Цепочки из T* - x,y,v,w,z.

Пример:

N={B,C,S},

T={a,b}.

P: 1. S→aCa, 2. C→CBa, 3. C→b, 4. aB→Ba, 5. bB→bb.

1. S→⁽¹⁾aCa → ⁽³⁾ aba

2. S→⁽¹⁾aCa→⁽²⁾aCBaa→⁽³⁾abBaa→⁽⁵⁾abbaa.

Грамматики, для которых нет ограничений на правила множества P, называются грамматиками типа 0. Это самые общие грамматики. Языки, определяемые грамматиками этого типа, называются языками класса 0.

Можно строго доказать, что множества цепочек, определяемые грамматиками данного типа, являются перечислимыми множествами. Это означает следующее: если задана грамматика G и цепочка x и требуется построить алгоритм, который бы определял справедливость высказывания , то существует алгоритм, который при положительном ответе на заданный вопрос за конечное число шагов остановится, а при отрицательном ответе будет работать бесконечно долго.

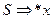Алгоритм таков: поскольку множество правил конечно, если , то существует вывод . Алгоритм будет перебирать все возможные правила, и, как только в результате этого встретится цепочка x, алгоритм прекратит свою работу. Здесь понадобится конечное, хотя и большое, число переборов. Накладывая различного рода ограничения, можно получить более простые грамматики, для которых указанная проблема разрешима, т.е. существует алгоритм, который для любой цепочки x останавливается, выдавая ответ “да” или “нет”. Подобного рода грамматики применяются на практике.

Если правила грамматики удовлетворяют следующему соотношению: , , 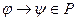то грамматика такого типа называется неукорачивающей, а языки, определяемые такими грамматиками, называются языками класса 1 (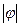– длина цепочки).

Проблема распознавания ставится следующим образом: задана грамматика G, цепочка 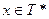. Требуется дать ответ: или 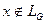. Если эта проблема разрешима, то язык распознаваемый.

Язык называется легко распознаваемым, если число шагов при решении проблемы распознавания зависит только от длины цепочки.

Теорема: Язык, определяемый неукорачивающей грамматикой, легко распознаваем.

Для доказательства этой теоремы мы должны построить алгоритм, который решает проблему распознавания, и число шагов зависит только от длины цепочки.

Доказательство: Пусть 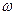- заданная цепочка длины 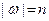. Рассмотрим возможный вывод этой цепочки 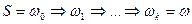. Если в выводе встречаются повторяющиеся участки вида 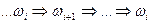, то мы можем исключить их. Выводы без таких исключаемых частей называют бесповторными. Т.к. длина цепочки фиксирована и равна n, то существует конечное число бесповторных выводов и алгоритм может быть таков: построить множество бесповторных выводов всевозможных цепочек длины n. В силу свойства грамматики длина каждой последующей цепочки в выводе не меньше длины предыдущей, такое множество может быть только конечным.

Далее предъявленную цепочку 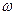необходимо сравнить с элементами построенного множества. Работа данного алгоритма (количество шагов) зависит только от длины цепочки.

Замечание: описанный алгоритм очень неэффективен и используется только для доказательства.

Дата добавления: 2014-02-26; просмотров: 554; Нарушение авторских прав

Мы поможем в написании ваших работ!