Использование сплайнов

Одним из методов численного интегрирования, особенно эффективным при строго ограниченном числе узлов, является метод сплайнов, использующий интерполяцию сплайнами.

Разобьем отрезок интегрирования на 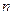частей точками 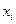. Пусть 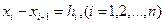. На каж­дом элементарном отрезке интерполируем подынтеграль­ную функцию с помощью кубического сплайна: 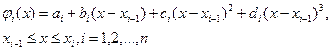(1).

Выражение для интеграла представим в виде .

Используя выражение (1), в результате вычисления интегралов находим (2).

Для практических расчетов формулу (2) можно представить в виде (3).

Анализ этой формулы показывает, что первый член в правой части совпадает с правой частью формулы для метода трапеций. Следовательно, второй член харак­теризует поправку к методу трапеций, которую дает ис­пользование сплайнов.

Как следует из формулы (1), коэффициенты выражаются через вторые производные :

.

Это позволяет оценить второй член правой части фор­мулы (3):

,

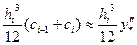где 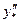- вторая производная в некоторой внутренней точке. Полученная оценка показывает, что добавка к фор­муле трапеций, которую дает использование сплайнов, компенсирует погрешность самой формулы трапеций.

Отметим, что во всех предыдущих методах формулы численного интегрирования можно условно записать в виде линейной комбинации табличных зна­чений функции:

.

При использовании сплайнов такое представление не­возможно, поскольку сами коэффициенты зависят от всех значений .

Рассмотрев разные методы численного интегрирова­ния, трудно сравнивать их достоинства и недостатки. Любая попытка такого сравнения непременно поставит перед нами альтернативный вопрос: что больше, 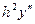или 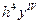? Все зависит от самой функции и поведения ее производных.

Уточнение результатов численного интегрирования можно проводить по-разному. В частности, в представленном на рисунке алгоритме с использованием метода Симпсона проводится сравнение двух значений интеграла и , полученных при разбиениях отрезка соот­ветственно с шагам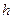и и . Аналогичный алгоритм можно построить и для других методов.

Здесь мы упомянем другую схему уточнения значе­ния интеграла - процесс Эйткена. Он дает возможность оценить погрешность метода и указывает алгоритм уточнения результатов. Расчет проводится последователь­но три раза при различных шагах разбиения 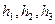, причем их отношения постоянны:

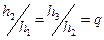
(на­пример, при делении шага пополам ). Пусть в результате численного интегрирования получены значе­ния интеграла 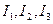. Тогда уточненное значение ин­теграла вычисляется по формуле:

,

а порядок точности используемого метода численного интегрирования определяется соотношением .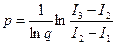

Уточнение значения интеграла можно также проводить методом Рунге — Ромберга .

Адаптивные алгоритмы.

Из анализа погрешностей методов численного интегрирования следует, что точность получаемых результатов зависит как от характера изме­нения подынтегральной функции, так и от шага интегри­рования. Будем считать, что величину шага мы задаем. При этом ясно, что для достижения сравнимой точности при интегрировании слабо меняющейся функции шаг можно выбирать большим, чем при интегрировании рез­ко меняющихся функций.

На практике нередко встречаются случаи, когда подынтегральная функция меняется по-разному на от­дельных участках отрезка интегрирования. Это обстоя­тельство требует такой организации экономичных чис­ленных алгоритмов, при которой они автоматически при­спосабливались бы к характеру изменения функции. Та­кие алгоритмы называются адаптивными (приспосабли­вающимися). Они позволяют вводить разные значения шага интегрирования на отдельных участках отрезка интегрирования. Это дает возможность уменьшить ма­шинное время без потери точности результатов расчета. Подчеркнем, что этот подход используется обычно при задании подынтегральной функции в виде фор­мулы, а не в табличном виде.

Программа, реализующая адаптивный алгоритм численного интегрирования, входит обычно в виде стандартной подпрограммы в математическое обеспечение ЭВМ. Пользователь готовой программы задает границы отрезка интегрирования , допустимую абсолютную погреш­ность 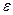и составляет блок программы для вычисления значения подынтегральной функции . Программа вычисляет значение интеграла 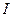с заданной погреш­ностью 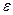, т. е.

(4).

Разумеется, не для всякой функции можно получить результат с заданной погрешностью. Поэтому в програм­ме может быть предусмотрено сообщение пользователю о недостижимости заданной погрешности. Интеграл при этом вычисляется с максимально возможной точностью, и программа выдает эту реальную точность.

Рассмотрим принцип работы адаптивного алгоритма. Первоначально отрезок разбиваем на 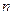частей. В дальнейшем каждый такой элементарный отрезок де­лим последовательно пополам. Окончательное число ша­гов, их расположение и размеры зависят от подынте­гральной функции и допустимой погрешности каждому элементарному отрезку 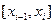приме­няем формулы численного интегрирования при двух различных его разбиениях. Получаем приближения для интеграла по этому отрезку:

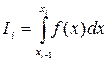(5).

Полученные значения сравниваем и проводим оценку их погрешности. Если погрешность находится в допустимых границах, то одно из этих приближений принимается за значение интеграла по этому элементарному отрезку. В противном случае происходит дальнейшее деление от­резка и вычисление новых приближений. С целью эко­номии машинного времени точки деления располагаются таким образом, чтобы использовались вычисленные зна­чения функции в точках предыдущего разбиения.

Например, при вычислении интеграла (5) по формуле Симпсона отрезок 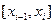сначала разбиваем на две части с шагом 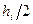и вычисляем значение . Потом вычисляем с шагом . Получим выражения

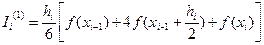(6),

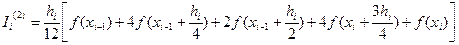(7).

Формулу (7) можно также получить двукратным при­менением формулы (6) для отрезков и .

Процесс деления отрезка пополам и вычисления уточненных значений и продолжается до тех пор, пока их разность станет не больше некоторой заданной величины 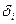, зависящей от 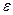и :

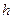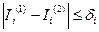(8).

Аналогичная процедура проводится для всех 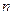элементарных отрезков. Величина принимается в качестве искомого значения интеграла. Условия (8) и соответствующий выбор величин 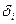обеспечивают вы­полнение условия (4).

Дата добавления: 2014-03-01; просмотров: 466; Нарушение авторских прав

Мы поможем в написании ваших работ!