Кратные интегралы

Численные методы использу­ются также для вычисления кратных интегралов. Огра­ничимся здесь рассмотрением двойных интегралов вида

(9).

Одним из простейших способов вычисления этого ин­теграла является метод ячеек. Рассмотрим сначала слу­чай, когда областью интегрирования является прямо­угольник: 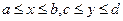. По теореме о среднем найдем среднее значение функции :

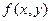, (10).

Будем считать, что среднее значение приближенно рав­но значению функции в центре прямоугольника, т, е. 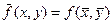. Тогда из (10) получим выражение для приближенного вычисления двойного интеграла:

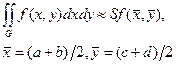(11).

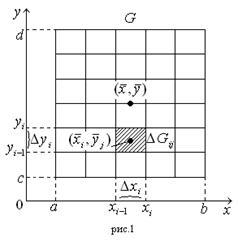Точность этой формулы можно повысить, если разбить область на прямоугольные ячейки (рис. 1): 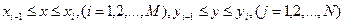. Применяя к каждой ячейке формулу (11), получаем

.

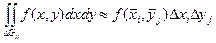Суммируя эти выражения по всем ячейкам, находим зна­чение двойного интеграла:

(12).

В правой части стоит интегральная сумма; поэтому при неограниченном уменьшении периметров ячеек (или стя­гивании их в точки) эта сумма стремится к значению интеграла для любой непрерывной функции .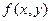

Можно показать, что погрешность такого приближе­ния интеграла для одной ячейки оценивается соотноше­нием

.

Суммируя эти выражения по всем ячейкам и считая все их площади одинаковыми, получаем оценку погрешности метода ячеек в виде

.

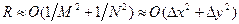Таким образом, формула (12) имеет второй порядок точности. Для повышения точности можно использовать обычные методы сгущения узлов сетки. При этом по каждой переменной шаги уменьшают в одинаковое число раз, т. е. отношение 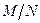остается постоянным.

Если область непрямоугольная, то в ряде случаев ее целесообразно привести к прямоугольному виду путем соответствующей замены переменных. Например, пусть область задана в виде криволинейного четырехугольника: 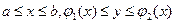. Данную область можно привести к прямоугольному виду с помощью замены

.

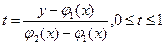Кроме того, формула (12) может быть обобщена и на случай более сложных областей.

Другим довольно распространенным методом вычис­ления кратных интегралов является их сведение к по­следовательному вычислению определенных интегралов.

Интеграл (9) для прямоугольной области можно за­писать в виде

, .

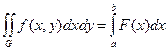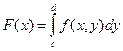Для вычисления обоих определенных интегралов могут быть использованы рассмотренные ранее численные ме­тоды.

Если область имеет более сложную структуру, то она либо приводится к прямоугольному виду с помощью замены переменных, либо разбивается на простые эле­менты.

Для вычисления кратных интегралов используется также метод замены подынтегральной функции много­мерным интерполяционным многочленом. Вычисление коэффициентов этих многочленов для простых областей обычно не вызывает затруднений.

Существует ряд других численных методов вычисле­ния кратных интегралов. Среди них особое место зани­мает метод статистических испытаний, который мы вкрат­це изложим.

Дата добавления: 2014-03-01; просмотров: 590; Нарушение авторских прав

Мы поможем в написании ваших работ!