Численное дифференцированно

Лекция 6.

Аппроксимация производных.

Напомним, что производной функции называется предел отноше­ния приращения функции 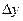к приращению аргумента при стремлении к нулю:

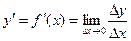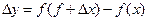, (1).

Обычно для вычисления производных используют го­товые формулы (таблицу производных) и к выражению (1) не прибегают. Однако в численных расчетах на ЭВМ использование этих формул не всегда удобно и возможно. В частности, функция может быть задана в виде таблицы значений. В таких случаях про­изводную находят, опираясь на формулу (1). Значение шага полагают равным некоторому конечному числу и для вычисления значения производной получают при­ближенное равенство

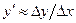(2).

Это соотношение называется аппроксимацией (при­ближением) производной с помощью отношения конеч­ных разностей (значения 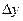, в формуле (2) конечные в отличие от их бесконечно малых значений в (1)).

Рассмотрим аппроксимацию производной для функ­ции , заданной в табличном виде: при 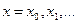. Пусть шаг - разность между соседними значениями аргумента - постоянный и равен 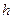. Запишем выражения для производно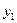й при . В зависимо­сти от способа вычисления конечных разностей получаем разные формулы для вычисления производной в одной и той же точке: , , 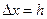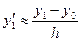(3) с помощью левых разностей;

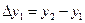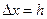, , (4) с помощью правых разностей;

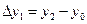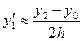, , (5) с помощью центральных разностей.

Можно найти также выражения для старших произ­водных. Например,

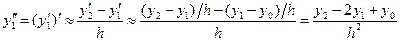(6).

Таким образом, по формуле (2) можно найти при­ближенные значения производных любого порядка. Одна­ко при этом остается открытым вопрос о точности полу­ченных значений. Кроме того, как будет показано ниже, для хорошей аппроксимации производной нужно исполь­зовать значения функции во многих узлах, а в формуле (2), это не предусмотрено.

Дата добавления: 2014-03-01; просмотров: 520; Нарушение авторских прав

Мы поможем в написании ваших работ!