Лекция 3. Дифференциальные уравнения

При описании динамики биологических систем математическими методами интересующие биологические переменные могут быть функциями таких переменных, как температура, обилие пищи, длина светового дня или частота заболеваний. Однако, мы ограничимся рассмотрением численности популяции некоторого вида в заданной среде как функции времени.

При описании биологических систем используются дискретные и непрерывные уравнения. Непрерывные уравнения больше подходят для описания роста очень больших популяций, таких, как, например, популяции бактерий. Напротив, популяции американского журавля лучше описываются разностными уравнениями, соответствующие ежедневным, ежемесячным или ежегодным их подсчетам.

В непрерывных уравнениях 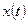представляет собой численность (размер) популяции некоторого вида в данной среде как функция времени. Исходной, или начальной популяции соответствует .

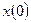При изучении непрерывного роста популяции 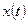нам может быть дана информация о скорости роста 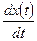. Скорость роста может быть, например, нулевой, т.е. 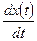=0.В этом случае сохраняется постоянный размер популяции.

Определение1.Дифференциальным уравнением для функции 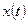называется уравнение, которое содержит производные 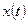по времени 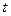. Порядок дифференциального уравнения определяется как наивысший порядок производных, встречающихся в записи уравнения.

Пример 1.Уравнение 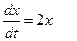- первого порядка; 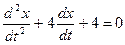- второго порядка;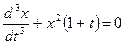- третьего порядка;

Пример 2. Популяция бактерий растет так, что скорость ее роста в момент 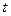(время выражается в часах) равна размеру популяции, поделенному на 10. Описать этот процесс роста дифференциальным уравнением. Каков порядок этого уравнения?

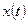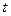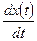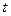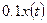Решение: Пусть размер популяции бактерий в момент времени . По условию задачи скорость роста в момент равна , т. е. 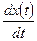=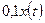. Это дифференциальное уравнение первого порядка для .

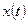Если дано дифференциальное уравнение для 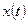, то можно найти все функции 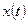, удовлетворяющие этому уравнению. Любая дифференцируемая функция, которая удовлетворяет дифференциальному уравнению, называется решением этого уравнения.

Пример 3.Дрожжи в растворе сахара растут таким образом, что их масса увеличивается со скоростью, равной половине массы в момент 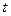(время выражается в часах). Опишите изменение массы дрожжей с помощью дифференциального уравнения. Каков порядок уравнения?

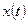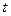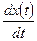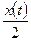Решение: Пусть масса популяции дрожжей в момент времени . По условию задачи скорость роста массы равна , т.е. 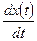=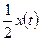. Это уравнение первого порядка.

Дата добавления: 2014-03-11; просмотров: 650; Нарушение авторских прав

Мы поможем в написании ваших работ!