
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Простейшие свойства кольца
Кольца
О. Кольцом называется алгебра 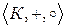 с двумя алгебраическими операциями, называемыми сложением и умножением, если выполняются следующие свойства:
с двумя алгебраическими операциями, называемыми сложением и умножением, если выполняются следующие свойства:
1) алгебра 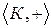 является абелевой группой, т.е.
является абелевой группой, т.е.
а) сложение коммутативно и ассоциативно;
б) имеется нулевой элемент, обозначаемый через 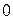 (
(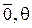 и т.п.);
и т.п.);
в) для каждого элемента 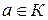 в
в 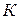 имеется противоположный ему элемент
имеется противоположный ему элемент 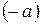 ;
;
2) умножение ассоциативно;
3) выполняется дистрибутивный закон умножения относительно сложения, т.е. для любых элементов  имеют место равенства
имеют место равенства 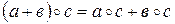 и
и 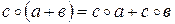 .
.
Если умножение в кольце 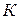 коммутативно, то кольцо называют коммутативным.
коммутативно, то кольцо называют коммутативным.
Если для умножения в кольце 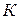 имеется единичный элемент, то кольцо называют кольцом с единицей. Единичный элемент
имеется единичный элемент, то кольцо называют кольцом с единицей. Единичный элемент 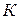 обозначают через
обозначают через 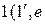 и т.п.).
и т.п.).
Отметим, что в некоторых источниках существование единичного элемента включается в определение кольца (см., например, [3]).
О. Алгебру 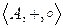 называют полукольцом, если в ней выполняются все условия определения кольца, за исключением существования противоположного элемента для произвольного элемента
называют полукольцом, если в ней выполняются все условия определения кольца, за исключением существования противоположного элемента для произвольного элемента 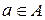 .
.
Примеры колец:
1. Непосредственно проверяется, что множество целых, рациональных и действительных чисел являются кольцами, но множество натуральных чисел 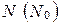 не является кольцом, но является полукольцом.
не является кольцом, но является полукольцом.
2. Пусть 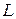 - некоторое числовое кольцо. Таблицу вида
- некоторое числовое кольцо. Таблицу вида 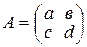 , где
, где 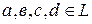 , называют квадратичной матрицей второго порядка над
, называют квадратичной матрицей второго порядка над 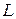 или матрицей размерности
или матрицей размерности 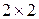 и пишут
и пишут 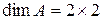 .
.
Множество всех квадратных матриц второго порядка над кольцом 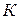 будем обозначать через
будем обозначать через 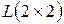 .
.
Две матрицы 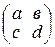 и
и 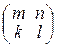 называют равными, если
называют равными, если 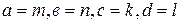 , и пишут
, и пишут 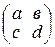 =
=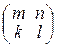 .
.
На множестве 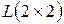 введем операции сложения и умножения следующим образом:
введем операции сложения и умножения следующим образом:
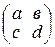 +
+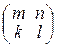 =
=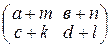 и
и 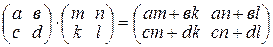 .
.
Очевидно, что указанные операции на этом множестве являются алгебраическими.
Покажем, что алгебра  является кольцом с единицей. Действительно:
является кольцом с единицей. Действительно:
1) сложение ассоциативно и коммутативно, т.е. имеют место равенства
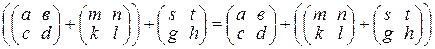 и
и 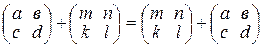
для любых матриц из 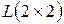 ;
;
2) имеется нулевой элемент, а именно, нулевая матрица 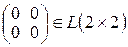 такая, что
такая, что
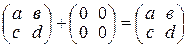 ;
;
3) для матрицы 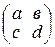 противоположной является матрица
противоположной является матрица 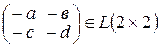 ;
;
4) умножение ассоциативно, т.е.
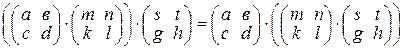 ;
;
5) единичным элементом является единичная матрица, т.е. матрица  , такая, что
, такая, что 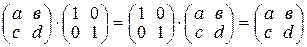 .
.
Выполнимость свойств 1-5 проверьте самостоятельно.
6) умножение матриц дистрибутивно относительно сложения, т.е. справедливы равенства:
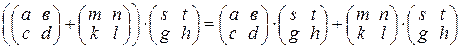 и
и
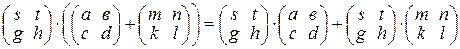 .
.
Проверим только выполнимость первого равенства, выполнимость второго проверяется аналогично (проверьте самостоятельно). Подсчитаем отдельно левые и правые части равенства:
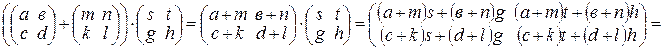
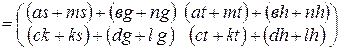 . (1)
. (1)
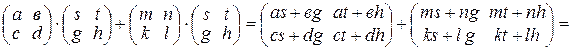
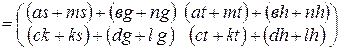 . (2)
. (2)
Правые части равенств (1) и (2) совпадают, стало быть, совпадают и левые части.
Итак, доказано, что 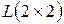 является кольцом с единицей.
является кольцом с единицей.
В качестве 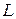 возьмем кольцо целых чисел
возьмем кольцо целых чисел 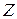 и рассмотрим произведения матриц
и рассмотрим произведения матриц
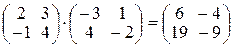 и
и  .
.
Этот пример показывает, что 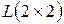 - некоммутативно, т.е.
- некоммутативно, т.е. 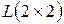 - в общем случае некоммутативное кольцо.
- в общем случае некоммутативное кольцо.
Так как число элементов кольца 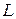 бесконечно, то и кольцо
бесконечно, то и кольцо 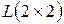 будет бесконечным.
будет бесконечным.
Упр. 13. Найдите произведения матриц 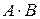 и
и 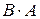 , где
, где 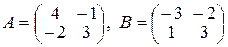 .
.
Пусть 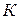 - кольцо. Укажем некоторые его простейшие свойства:
- кольцо. Укажем некоторые его простейшие свойства:
1) для любых  и
и  из
из 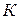 в нем разрешимо уравнение
в нем разрешимо уравнение 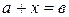 .
.
Действительно, существует  , прибавим к обеим частям уравнения
, прибавим к обеим частям уравнения 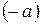 , тогда получим
, тогда получим  , но
, но 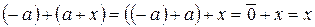 , где
, где 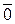 - нулевой элемент
- нулевой элемент 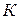 , или
, или 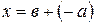 . Обычно вместо
. Обычно вместо 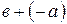 пишут
пишут 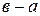 и называют этот элемент разностью
и называют этот элемент разностью  и
и  . По определению разности имеет место равенство
. По определению разности имеет место равенство 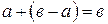 .
.
2) 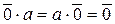 .
.
Действительно, 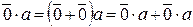 или
или 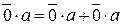 , получим
, получим 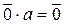 . Докажите, что
. Докажите, что 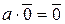 .
.
3) 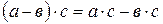 (распределительный закон умножения относительно вычитания).
(распределительный закон умножения относительно вычитания).
Д.: 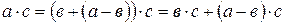 или
или 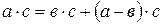 , к обеим частям прибавим
, к обеим частям прибавим 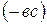 , получим
, получим 
 .
.
Аналогично доказывается, что  .
.
Следствие.  , т.к.
, т.к. 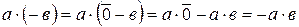 .
.
4) Пусть 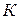 - кольцо с
- кольцо с 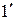 , тогда существует
, тогда существует 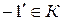 и выполняется равенство
и выполняется равенство 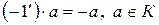 .
.
Действительно, 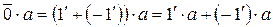 или, учитывая, что
или, учитывая, что 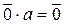 и
и 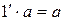 , будем иметь
, будем иметь 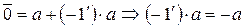 .
.
5) Докажите, что имеют место равенства для любых 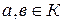 :
:
а) 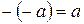 ; б)
; б)  ; в)
; в) 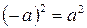 .
.
Подкольца. Пусть 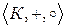 - кольцо.
- кольцо.
О. Подмножество 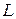 кольца
кольца 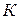 называется его подкольцом, если
называется его подкольцом, если 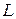 само является кольцом относительно операций, определенных в кольце
само является кольцом относительно операций, определенных в кольце 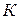 .
.
Теорема (критерий подкольца). Подмножество 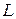 кольца
кольца 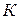 тогда и только тогда является его подкольцом, если выполняются следующие два условия:
тогда и только тогда является его подкольцом, если выполняются следующие два условия:
1) для любых  и
и  из
из 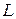
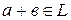 и
и 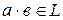 , т.е. операции сложения и умножения замкнуты на
, т.е. операции сложения и умножения замкнуты на 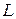 ;
;
2)  .
.
Необходимость и достаточность условий теоремы очевидны, докажите самостоятельно.
Упр. 14. Дано 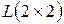 - кольцо квадратных матриц с элементами из числового кольца
- кольцо квадратных матриц с элементами из числового кольца 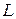 . Матрицу вида
. Матрицу вида 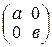 ,
, 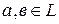 , называют диагональными, а матрицу вида
, называют диагональными, а матрицу вида 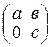 - верхнетреугольной. Докажите, что: а) множество всех диагональных матриц
- верхнетреугольной. Докажите, что: а) множество всех диагональных матриц 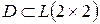 ; б) множество всех верхнетреугольных матриц
; б) множество всех верхнетреугольных матриц 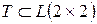 являются подкольцами кольца
являются подкольцами кольца 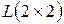 .
.
Упр. 15. Докажите, что множество 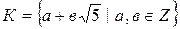 образует кольцо.
образует кольцо.
Упр. 16. Образует ли кольцо множество отрицательных целых чисел с добавлением нуля?
| <== предыдущая страница | | | следующая страница ==> |
| Подгруппы | | | Натуральные числа |
Дата добавления: 2014-03-11; просмотров: 614; Нарушение авторских прав

Мы поможем в написании ваших работ!