Геометрическое определение вероятности

Классическое определение вероятности.

Определение: вероятностью события А называют отношение числа благоприятных исхо­дов при которых появляется событие А к общему числу исходов которые образуют пол­ную группу.

Р(А)=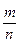

m - число исходов благоприятствующих наступлению события А; n - общее число исходов образующих полную группу.

Следствие:

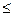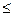1. Вероятность наступления события А число большее либо равное нулю, 0Р(А)1.

2. Вероятность достоверного события А равна 1, Р(А) = 1.

3. Вероятность невозможного события А равна 0, Р(А) = 0.

Классическое определение вероятности имеет свои недостатки. Оно неприменимо тогда, когда в испытании возможно бесконечное число исходов, в этом случае применяют гео­метрическое определение вероятности, т.е. вероятность попадания точки в какую - либо область.

Р(А) =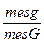

где g - измерение в заданной области.

Найти вероятность попадания точки в область 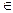s S :

S

s

Замечание:в случае классического определения вероятность достоверного события равна 1, вероятность невозможного события равна 0. Обратно: если вероятность события равна 0, то событие невозможно. В случае геометрической вероятности утверждать обратное нельзя, т.е. вероятность попадания точки в заданную точку равна 0, с другой стороны оно не является невозможным.

Дата добавления: 2014-02-26; просмотров: 696; Нарушение авторских прав

Мы поможем в написании ваших работ!