Supersymmetry and the weak scale

Date: 2015-10-07; view: 604.

Once supersymmetry is broken, the mass scale for superpartners is unconstrained. There is, however, a strong motivation for this scale to be the weak scale: the gauge hierarchy problem. In the standard model of particle physics, the classical mass of the Higgs boson 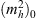receives quantum corrections (see Fig. 1). Including quantum corrections from standard model fermions f_L and f_R, one finds that the physical Higgs boson mass is

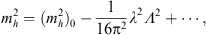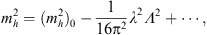
(5)

where the last term is the leading quantum correction, with λ the Higgs-fermion coupling. Λ is the ultraviolet cutoff of the loop integral, presumably some high scale well above the weak scale. If Λ is of the order of the Planck scale 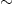10¹⁹ GeV, the classical Higgs mass and its quantum correction must cancel to an unbelievable 1 part in 10³⁴ to produce the required weak-scale m_h. This unnatural fine-tuning is the gauge hierarchy problem.

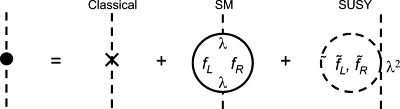
Fig. 1. Contributions to the Higgs boson mass in the standard model and in supersymmetry.

In the supersymmetric standard model, however, for every quantum correction with standard model fermions f_L and f_R in the loop, there are corresponding quantum corrections with superpartners 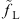and 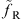. The physical Higgs mass then becomes

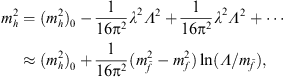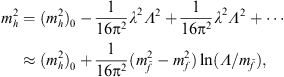
(6)

where the terms quadratic in Λ cancel, leaving a term logarithmic in Λ as the leading contribution. In this case, the quantum corrections are reasonable even for very large Λ, and no fine-tuning is required.

In the case of exact supersymmetry, where 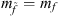, even the logarithmically divergent term vanishes. In fact, quantum corrections to masses vanish to all orders in perturbation theory, an example of powerful non-renormalization theorems in supersymmetry. From Eq. (6), however, we see that exact mass degeneracy is not required to solve the gauge hierarchy problem. What is required is that the dimensionless couplings λ of standard model particles and their superpartners are identical, and that the superpartner masses be not too far above the weak scale (or else even the logarithmically divergent term would be large compared to the weak scale, requiring another fine-tuned cancellation). This can be achieved simply by adding supersymmetry-breaking weak-scale masses for superpartners. In fact, other terms, such as some cubic scalar couplings, may also be added without re-introducing the fine-tuning. All such terms are called “soft,” and the theory with weak-scale soft supersymmetry-breaking terms is “weak-scale supersymmetry.”