
Freeze out and WIMPs
Date: 2015-10-07; view: 670.
Dark matter may be produced in a simple and predictive manner as a thermal relic of the Big Bang. The very early universe is a very simple place—all particles are in thermal equilibrium. As the universe cools and expands, however, interaction rates become too low to maintain this equilibrium, and so particles “freeze out.” Unstable particles that freeze out disappear from the universe. However, the number of stable particles asymptotically approaches a non-vanishing constant, and this, their thermal relic density, survives to the present day.
This process is described quantitatively by the Boltzmann equation

| (18) |
where n is the number density of the dark matter particle χ, H is the Hubble parameter,  σAv
σAv  is the thermally averaged annihilation cross-section, and neq is the χ number density in thermal equilibrium. On the right-hand side of Eq. (18), the first term accounts for dilution from expansion. The n2 term arises from processes
is the thermally averaged annihilation cross-section, and neq is the χ number density in thermal equilibrium. On the right-hand side of Eq. (18), the first term accounts for dilution from expansion. The n2 term arises from processes 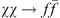 that destroy χ particles, and the
that destroy χ particles, and the  term arises from the reverse process
term arises from the reverse process  , which creates χ particles.
, which creates χ particles.
It is convenient to change variables from time to temperature,

| (19) |
where m is the χ mass, and to replace the number density by the co-moving number density

| (20) |
where s is the entropy density. The expansion of the universe has no effect on Y, because s scales inversely with the volume of the universe when entropy is conserved. In terms of these new variables, the Boltzmann equation is

| (21) |
In this form, it is clear that before freeze out, when the annihilation rate is large compared with the expansion rate, Y tracks its equilibrium value Yeq. After freeze out, Y approaches a constant. This constant is determined by the annihilation cross-section  σAv
σAv  . The larger this cross-section, the longer Y follows its exponentially decreasing equilibrium value, and the lower the thermal relic density. This behavior is shown in Fig. 7.
. The larger this cross-section, the longer Y follows its exponentially decreasing equilibrium value, and the lower the thermal relic density. This behavior is shown in Fig. 7.


Fig. 7. The co-moving number density Y of a dark matter particle as a function of temperature and time. From [16].

Let us now consider WIMPs—weakly interacting massive particles with mass and annihilation cross-section set by the weak scale:  . Freeze out takes place when
. Freeze out takes place when
neq  σAv σAv  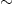 H. H.
| (22) |
Neglecting numerical factors, neq 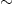 (mT)3/2e−m/T for a non-relativistic particle, and H
(mT)3/2e−m/T for a non-relativistic particle, and H 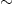 T2/M
T2/M  . From these relations, we find that WIMPs freeze out when
. From these relations, we find that WIMPs freeze out when

| (23) |
Since  , WIMPs freeze out with velocity v
, WIMPs freeze out with velocity v 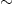 0.3.
0.3.
One might think that, since the number density of a particle falls exponentially once the temperature drops below its mass, freeze out should occur at T 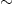 m. This is not the case. Because gravity is weak and M
m. This is not the case. Because gravity is weak and M  is large, the expansion rate is extremely slow, and freeze out occurs much later than one might naively expect. For a m
is large, the expansion rate is extremely slow, and freeze out occurs much later than one might naively expect. For a m 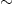 300 GeV particle, freeze out occurs not at T
300 GeV particle, freeze out occurs not at T 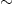 300 GeV and time t
300 GeV and time t 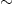 10−12 s, but rather at temperature T
10−12 s, but rather at temperature T 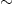 10 GeV and time t
10 GeV and time t 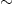 10−8 s.
10−8 s.
With a little more work [17], one can find not just the freeze out time, but also the freeze out density

| (24) |
A typical weak cross-section is

| (25) |
corresponding to a thermal relic density of Ωh2 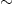 0.1. WIMPs therefore naturally have thermal relic densities of the observed magnitude. The analysis above has ignored many numerical factors, and the thermal relic density may vary by as much as a few orders of magnitude. Nevertheless, in conjunction with the other strong motivations for new physics at the weak scale, this coincidence is an important hint that the problems of electroweak symmetry breaking and dark matter may be intimately related.
0.1. WIMPs therefore naturally have thermal relic densities of the observed magnitude. The analysis above has ignored many numerical factors, and the thermal relic density may vary by as much as a few orders of magnitude. Nevertheless, in conjunction with the other strong motivations for new physics at the weak scale, this coincidence is an important hint that the problems of electroweak symmetry breaking and dark matter may be intimately related.
| <== previous lecture | | | next lecture ==> |
| Neutralino cosmology | | | Thermal relic density |