
Spacetime algebra and Dirac theory
Date: 2015-10-07; view: 605.
Just as it is possible to describe geometric algebra as a fermionic deformed superanalysis it is also possible to describe spacetime algebra in this context. The basis vectors of space-time are the Grassmann elements γ0, γ1, γ2, and γ3, which fulfill
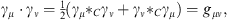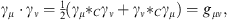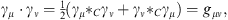
| (6.1) |
where we choose here gμν = diag(1, −1, −1, −1). The corresponding Clifford star product in space-time is
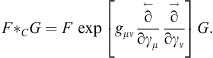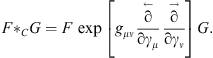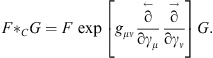
| (6.2) |
A general supernumber in space-time has the form
| A=a0+aμγμ+aμνγμγν+aμνργμγνγρ+a4I4, | (6.3) |
where I4 = γ0γ1γ2γ3 and only linearly independent terms should appear. With the four-dimensional pseudoscalar I4 and the Clifford star product (6.2) it is possible to construct analogously to (3.36) the dual basis γμ, which gives γ0 = γ0 and γi = −γi. Furthermore one can define in analogy to the three-dimensional case a trace:
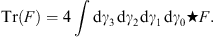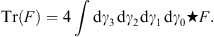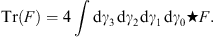
| (6.4) |
The Berezin integral acts here again like a projector on the scalar part of F. The definition of the trace by projecting on the scalar part was already given in [19] and it was also stated that the use of geometric algebra greatly simplifys all the trace calculations usually done in the matrix formalism. An explicit expression for the trace can now in the formalism of deformed superanalysis be given by the Berezin integral.
The question is now how a spacetime vector x=xμγμ is related to its space vector part x=xiσi. In the γ0-system this can be seen by a space-time split which amounts to star-multiplying by γ0:
x  Cγ0=x·γ0+xγ0=t+x. Cγ0=x·γ0+xγ0=t+x.
| (6.5) |
One should note that x=xγ0=x1γ1γ0+x2γ2γ0+x3γ3γ0 is a spacetime bivector, but on the other hand it is also a space vector because the two-blades γiγ0 behave like σi:
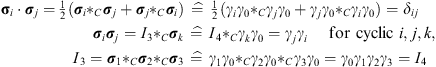
| (6.6) |
where the four-dimensional star product (6.2) and the three-dimensional star product (3.14) is used in (6.6), as should be clear from the context. The square of the position four vector is x2  C=t2-x2
C=t2-x2  C.
C.
If a particle is moving in the γ0-system along x (τ), where τ is the proper time, the proper velocity is given by 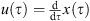 , with u2
, with u2  C=1. For the space-time split of the proper velocity one obtains:
C=1. For the space-time split of the proper velocity one obtains:
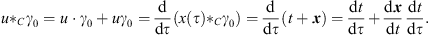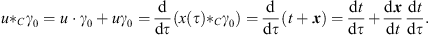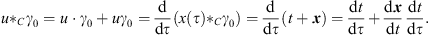
| (6.7) |
Comparing the scalar and the bivector part leads to
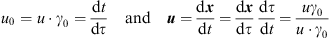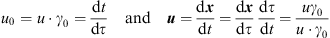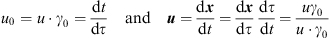
| (6.8) |
and with 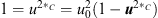 one gets [3]
one gets [3]
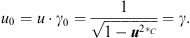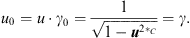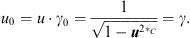
| (6.9) |
It is now also possible to specify a Lorentz transformation from a coordinate system γμ to a coordinate system 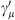 moving in the γ1-direction. For the coefficients this transformation is given by t = γ (t′ + βx′1), x1 = γ (x′1 + βt′), x2 = x′2, and x3 = x′3. The condition
moving in the γ1-direction. For the coefficients this transformation is given by t = γ (t′ + βx′1), x1 = γ (x′1 + βt′), x2 = x′2, and x3 = x′3. The condition 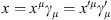 leads then to
leads then to
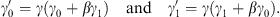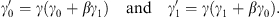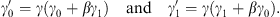
| (6.10) |
Introducing the angle α so that β = tanh (α) this can be written as
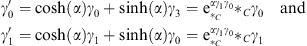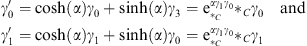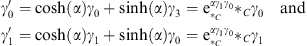
| (6.11) |
or with 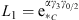 as
as 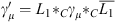 . In general the generators of a passive Lorentz transformation can be calculated with
. In general the generators of a passive Lorentz transformation can be calculated with
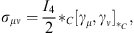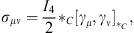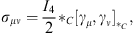
| (6.12) |
so that the generators for the boosts and the rotations are
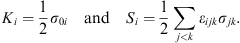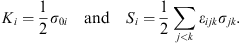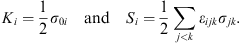
| (6.13) |
These generators satisfy
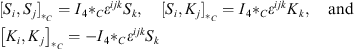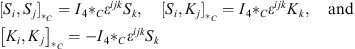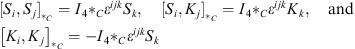
| (6.14) |
and a passive Lorentz transformation is given by
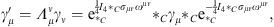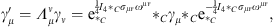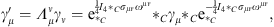
| (6.15) |
which is a generalization of (6.11).
The Dirac equation can then be written down immediately as [7]
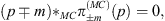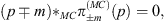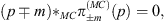
| (6.16) |
where no slash notation is needed, because one naturally has p=pμγμ. The Wigner function 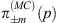 for the Dirac equation is the functional analog of the well-known energy projector of Dirac theory:
for the Dirac equation is the functional analog of the well-known energy projector of Dirac theory:
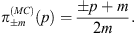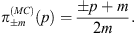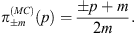
| (6.17) |
Besides the energy one also has the spin as an observable, which is here given by
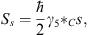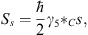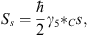
| (6.18) |
where s=sμγμ is a vector which fulfills s2  C=-1 and s · p = 0. γ5 is here γ5 = iI4. With
C=-1 and s · p = 0. γ5 is here γ5 = iI4. With 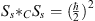 and [Ss,p
and [Ss,p 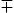 m]
m]  C=0 one sees that the spin Wigner function is given by the functional analog of the spin projector in Dirac theory
C=0 one sees that the spin Wigner function is given by the functional analog of the spin projector in Dirac theory
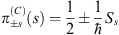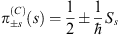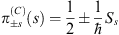
| (6.19) |
and fulfills 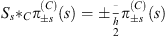 . The total Wigner function is then the Clifford star product of the two single Wigner functions.
. The total Wigner function is then the Clifford star product of the two single Wigner functions.
| <== previous lecture | | | next lecture ==> |
| Non-relativistic quantum mechanics | | | Conclusions |