The one-arm exponent

Date: 2015-10-07; view: 450.

Consider critical lattice percolation inside some finite region (for example a disc of radius R). What is the probability that a given site (e.g., the origin) is connected to a finite segment S of the boundary? This should decay like R^−λ, where λ is sometimes called the one-arm exponent. If we try to formulate this in the continuum, we immediately run up against the problem that all clusters are fractal with dimension <2, and so the probability of any given point being in any given cluster is zero. Instead, one may ask about the probability P (r) that the cluster connected to S gets within a distance r of the origin. This should behave like (r/R)^λ. We can now set R = 1 and treat the problem using radial SLE₆.

Consider now a radial SLE_κ which starts at e^iθ₀. If κ > 4 it will continually hit the boundary. Let P (θ − θ₀, t) be the probability that the segment (θ₀, θ) of the boundary has not been swallowed by time t. Then, by considering the evolution as usual under g_dt

P(θ,θ0,t)= P(θ+dθ,θ0+dθ0,t-dt) ,

(38)

where dθ = cot((θ − θ₀)/2) dt and . Setting θ₀ = 0 and equating to zero the O (dt) term, we find the time-dependent differential equation

(39)

This has the form of a backwards Fokker–Plank equation.

Now, since , it is reasonable that, after time t, the SLE gets within a distance O (e^−t) of the origin. Therefore, we can interpret P as roughly the probability that the cluster connected to (0, θ) gets within a distance r 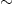e^−t of the origin. A more careful argument [32] confirms this. The boundary conditions are P (0, t) = 0 as θ → 0, and (with more difficulty) &#x2202;_θP (θ, t) = 0 at θ = 2π. The solution may then be found by inspection to be

P e-λt(sin(θ/4))1-4/κ,

(40)

where λ = (κ²−16)/32κ. For percolation this gives 5/48, in agreement with Coulomb gas arguments [3].

The appearance of differential operators such as that in (39) will become clear from the CFT perspective in Section 5.4.1. If instead of choosing Neuman boundary conditions at θ = 2π we impose P = 0, the same equation gives the bulk two-leg exponent x₂, which is also related to the fractal dimension by d_f = 2− x₂.