
Calogero–Sutherland model
Date: 2015-10-07; view: 620.
While many of the results of SLE may be re-derived in CFT with less rigour but perhaps greater simplicity, the latter contains much more information which is not immediately apparent from the SLE perspective. For example, one may consider correlation functions 
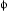 1,2 (r1)
1,2 (r1) 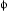 1,2 (r2)
1,2 (r2) 
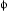 2,1 (rN)
2,1 (rN) 
 of multiple boundary condition changing operators with other operators either in the bulk or on the boundary. Evaluating the effect of an insertion (1/2πi)∫Γ T (z) dz/(z − rj) where Γ surrounds rj leads to a second order differential equation satisfied by the correlation function for each j.
of multiple boundary condition changing operators with other operators either in the bulk or on the boundary. Evaluating the effect of an insertion (1/2πi)∫Γ T (z) dz/(z − rj) where Γ surrounds rj leads to a second order differential equation satisfied by the correlation function for each j.
This property is very powerful in the radial version. Consider the correlation function
CΦ(θ1,…,θN)=  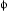 2,1(θ1) 2,1(θ1)  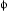 2,1(θN)Φ(0) 2,1(θN)Φ(0) 
| (61) |
of N 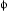 2,1 operators on the boundary of the unit disc with a single bulk operator Φ at the origin. Consider the effect of inserting (1/2πi)∫Γ αj (z)T (z) dz, where (cf. (26))
2,1 operators on the boundary of the unit disc with a single bulk operator Φ at the origin. Consider the effect of inserting (1/2πi)∫Γ αj (z)T (z) dz, where (cf. (26))

| (62) |
and Γ surrounds the origin. Once again, this may be evaluated in two ways: by taking Γ up to the boundary, with exception of small semicircles around the points eiθk, we get GjCΦ, where Gj is the second order differential operator

| (63) |
The first three terms come from evaluating the contour integral near eiθj, where αj acts like  (the term
(the term  comes from the curvature of the boundary), and the term with k ≠ j from the contour near eiθk, where it acts like
comes from the curvature of the boundary), and the term with k ≠ j from the contour near eiθk, where it acts like  .
.
On the other hand, shrinking the contour down on the origin we see that αj (z) = z + O (z2), so that on Φ (0) it has the effect of  , where the omitted terms involve the Ln and
, where the omitted terms involve the Ln and  with n > 0. Assuming that Φ is primary, these other terms vanish, leaving simply
with n > 0. Assuming that Φ is primary, these other terms vanish, leaving simply  . Equating the two evaluations we find the differential equation
. Equating the two evaluations we find the differential equation
| GjCΦ=xΦCΦ. | (64) |
In general there is an (N − 1)-dimensional space of independent differential operators Gj with a common eigenfunction CΦ. (There is one fewer dimension because they all commute with the total angular momentum ∑j(∂/∂θj).) For the case N = 2, setting θ = θ2 − θ1, we recognise the differential operator in Section 4.3.3.
In general these operators are not self-adjoint and their spectrum is difficult to analyse. However, if we form the equally weighted linear combination  , the terms with a single derivative may be written in the form ∑k(∂V/∂θk) (∂/∂θk) where V is a potential function. In this case it is well known from the theory of the Fokker–Plank equation that G is related by a similarity transformation to a self-adjoint operator. In fact [36] if we form |ΨN|2/κG|ΨN|−2/κ, where ΨN=∏j<k(eiθj-eθk) is the ‘free-fermion' wave function on the circle, the result is, up to calculable constants the well-known N-particle Calogero–Sutherland hamiltonian
, the terms with a single derivative may be written in the form ∑k(∂V/∂θk) (∂/∂θk) where V is a potential function. In this case it is well known from the theory of the Fokker–Plank equation that G is related by a similarity transformation to a self-adjoint operator. In fact [36] if we form |ΨN|2/κG|ΨN|−2/κ, where ΨN=∏j<k(eiθj-eθk) is the ‘free-fermion' wave function on the circle, the result is, up to calculable constants the well-known N-particle Calogero–Sutherland hamiltonian

| (65) |
with β = 8/κ. It follows that the scaling dimensions of bulk operators like Φ are simply related to eigenvalues ΛN of HN by

| (66) |
where  . Similarly CΦ is proportional to the corresponding eigenfunction. In fact the ground state (with conventional boundary conditions) turns out to correspond to the bulk N-leg operator discussed in Section 2.4.2. The corresponding correlator is |ΨN|2/κ.
. Similarly CΦ is proportional to the corresponding eigenfunction. In fact the ground state (with conventional boundary conditions) turns out to correspond to the bulk N-leg operator discussed in Section 2.4.2. The corresponding correlator is |ΨN|2/κ.
| <== previous lecture | | | next lecture ==> |
| Differential equations | | | Multiple SLEs |