Правила действий над матрицами.

Date: 2015-10-07; view: 425.

Матрицы. Основные понятия. Правило действий над матрицами.

Основные свойства алгебраического дополнения связаны по элементам разложения определенного столбца или строки.

По элементам i-й строки:

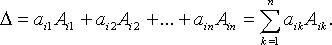
По элементам j-го столбца:

Например, при n = 4 разложение по первой строке

Матрица- это упорядоченная таблица элементов

Матрица состоит из строк и столбцов.

Основные понятия и обозначения. Пусть m и n два произвольных натуральных числа. Матрицей размера m на n (записывается так )называется совокупность mn вещественных (комплексных) чисел или элементов другой структуры (многочлены, функции и т.д.), При этом сами числа называются элементами матрицы и каждому элементу ставится в соответствие два числа - номер строки и номер столбца.

Для обозначения матрицы используются прописные латинские буквы, при этом саму матрицу заключают в круглые скобки.

Заметим, что для каждого размера существует своя нулевая матрица.

Матрица размера n на n называется квадратной матрицей n-го порядка, т.е. число строк равно числу столбцов.

Квадратная матрица называется диагональной, если все ее внедиагональные элементы равны нулю.

Диагональная матрица, у которой все диагональные элементы равны 1, называется единичной матрицей и обозначается символом I или E.

Матрица размера называется матрицей-строкой или вектор-строкой. Матрица размера называется матрицей столбцом или вектор-столбца