Interpretation of the population standard deviation

Date: 2015-10-07; view: 362.

Often in statistical studies we are interested in specifying the percentage of items in a data set that lie within some specified interval when only the mean and standard deviation for the data set are known. Two rules are commonly used for forming such estimates.

The first is true for any data set.

Chebyshev'stheorem:

For any set of data and any 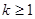, at least 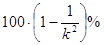of the values in the data set must be within plus or minus 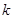standard deviations of the mean.

Remark:

In applying Chebyshev's theorem we treat every data set as if it were a population, and the formula for a population standard deviation is used.

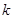
	1.5		2.5
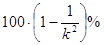
	55.6%	75%	84%

According to Chebyshev's rule, at least 55.6% of the population data lie within 1.5 standard deviations around the mean, at least 75% of the population data lie within 2 standard deviations around the mean and so on.

Example:

Let ,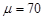

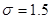
If we let 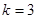from 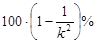we obtain that .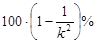

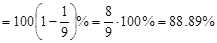The theorem states that at least 88.89% of data values will fall within 3 standard deviations of the mean. 88.89% of data falls within 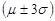or

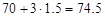and

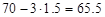
For 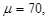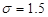, at 88.89% of the data values fall between 74.5, 65.5.