
The interquartile range
Date: 2015-10-07; view: 483.
Quartiles are the summary measures that divide a ranked data set into four equal parts. Three measures will divide any data set into four equal parts. These three measures are the first quartile (denoted by 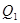 ), the second quartile (denoted by
), the second quartile (denoted by 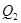 ), and the third quartile (denoted by
), and the third quartile (denoted by 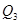 ). The data should be ranked in increasing order before the quartiles are determined. The quartiles are defined as follows:
). The data should be ranked in increasing order before the quartiles are determined. The quartiles are defined as follows:
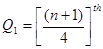 - ordered observation
- ordered observation
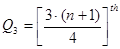 - ordered observation.
- ordered observation.
The difference between the third and the first quartiles gives the interquartile range. That is
 .
.
Example:
A teacher gives a 20-point test to 10 students. The scores are shown below
18, 15, 12, 6, 8, 2, 3, 5, 20, 10
Find the interquartile range.
Solution:
First, we rank the given data in increasing order:
2, 3, 5, 6, 8, 10, 12, 15, 18, 20
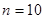
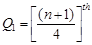 - ordered observation.
- ordered observation.
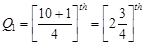 .
.
Hence, the first quartile is three-quarter way from the 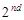 data (3) to the
data (3) to the 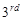 third (5). Therefore,
third (5). Therefore,
First quartile= 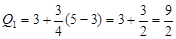
Similarly, since 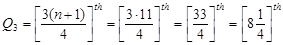
The third quartile is one-quarter of the way from the 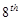 observation (15) to the
observation (15) to the 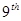 observation (18). Thus we have
observation (18). Thus we have
Third quartile= 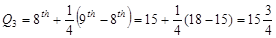 .
.
Finally, the interquartile range is the difference between the third and first quartiles:
Interquartile range= 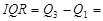
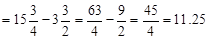
Example:
The following are the ages of nine employees of an insurance company
47, 28, 39, 51, 33, 37, 59, 24, 33
Find the interquartile range.
Solution:
Let us arrange the data in order from smallest to largest
24, 28, 33, 33, 37, 39, 47, 51, 59
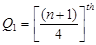
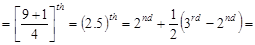
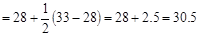
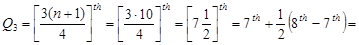
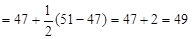
The interquartile range is
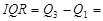
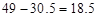 .
.
| <== previous lecture | | | next lecture ==> |
| Rule of Thumb. | | | Exercises |