
Алгебраические операции
Date: 2014-03-11; view: 1194.
Введение в числовые системы
Алгебраические операции. Алгебры.
Глазов 2007
Тексты лекций по алгебре
Обучения математике
Кафедра алгебры, геометрии, теории и методики
Література
• Базова:
1. Бойко О. Д. Історія України. –К.,2010
2. Грицак Я. Нарис історії України і формування модерної української нації. – К.: Генеза, 2010. – 250 с.
3. Історія України:Документи. Матеріали. Посібник / Уклад., комент. В. Ю. Короля . – К.: Видавничий центр «Академія», 2012. – 448 с.
4. Історія України в ХХ столітті ( 1900 – 2000): Зб. Документів і матеріалів / Упоряд. : А.Г.Слюсаренко та ін. – К.: Вища школа, 2011.- 351 с.
5. Історія України / за ред. Зайцев Ю.Д. – К.: Світ, 2003
6. Історія України / за ред. Кульчицький С.В., Лебедєва Ю. Г.. – К.:Освіта, 2003
7. Історія України / за ред. Кульчицький С.В., Шаповал Ю. І. – К.: Генеза, 2005;
8. Лазарович М. В. Історія України: Навч. посіб. – К.: Знання, 2008. – 683 с.
9. Мицик Ю. А. Історія України. –К., 2008
10. Новітня історія України ( 1900 – 2000 ) / Під ред. Слюсаренко А. Г. – 2 – ге вид. - К.: Вища школа, 2012. – 719 с.
11. Островський В.В. Історія України. - К.,2011
12. Середницька Г. В. Історія України: 10 кл.: опорні конспекти.- К: Книги України, 2012. – 382 с.
13. Середницька Г. В. Історія України: 11 кл.: опорні конспекти.- К: Книги України, 2012. – 320 с.
14. Субтельний О. Україна: історія. – К.:Либідь, 1993. – 720 с.
15. Чуткий А. І. Історія України: Навч. посіб. для студ. вищ. навч. закл. — К.: МАУП, 2006. — 352 с.
• Допоміжна:
16. Історія України: Навч. посіб. / Під ред. Ю. А. Мицик. – К.: Вид. дім «Києво – Могилянська академія», 2008. – 591 с.
17. Історія України у визначеннях, таблицях і схемах. 10 – 11 кл. / за ред.. Марченко О. С. – Х.: Вид – во «Ранок», 2011. – 112 с.
18. Історія України / за ред. Світлична В.В. - К., 2010
19. Історія України / за ред. Гончарук П.С. - К., 2009
20. Історія України / за ред. Гусєв В.І. - К., 2010
21. Історія України / за ред. Юрій М.Ф. - К., 2011
22. Лазарович М. В. Історія України: Навч. посіб. – К.: Знання, 2008. – 683с.
23. Новий довідник: Історія України. – К.: ТОВ « КАЗКА », 2012.- 736 с.
Викладач ___________ О. І. Винник
(для студентов первого курса математического факультета)
Методическая разработка по алгебре предназначена для студентов первого курса математического факультета по специальности 032100.01 – «Математика» с дополнительной специальностью «Информатика».
Составитель: канд. физ.-мат. наук, доцент Г.Г. Щепин
Будем рассматривать только непустые множества и считать известными понятия декартового произведения, отношения, заданного на одном или нескольких множествах. Воспользуемся стандартными сокращениями:
1) определение – О;
2) доказательство – Д.
В процессе развития науки, включая и математику, содержание предмета алгебры менялось. Примерно до середины 19 века в исследованиях по алгебре значительное место занимали вопросы, связанные с решением уравнений, неравенств и их систем, совершенствованием методов их приближенных решений. К указанным вопросам тесно примыкают теория матриц, определителей и некоторые другие теории.
Начиная с середины 19 века, точнее со второй его половины, алгебра, являющаяся, по выражению академика А.И. Мальцева (1909-1967), наиболее подвижной частью математики, получает мощный толчок в своем развитии. Существенно меняется характер ее исследований.
Основным предметом изучения алгебры становятся множества с заданными на них алгебраическими операциями, так называемые универсальные алгебры. В настоящее время предмет алгебры уже принято понимать в более широком смысле, а именно, - изучение множеств с определенными на них алгебраическими операциями и отношениями, называемых алгебраическими системами.
О. Говорят, что на множестве М задана бинарная алгебраическая операция или просто бинарная операция 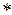 , если указано правило, сопоставляющее произвольной паре элементов а и в из М, взятым в определенном порядке, однозначно определенный элемент с из этого же множества М и обозначается
, если указано правило, сопоставляющее произвольной паре элементов а и в из М, взятым в определенном порядке, однозначно определенный элемент с из этого же множества М и обозначается 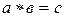 .
.
Возможны и другие обозначения операции, например,  или Т, т.е.
или Т, т.е. 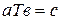 (
(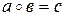 ).
).
Формально эту операцию можно рассматривать как отображение декартова произведения М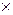 М в М.
М в М.
Различают нульместную (нулярную) и унарную операции.
О. Нульместной операцией на множестве М называют выделение (фиксирование) какого-нибудь элемента из М, причем каждая нульместная операция фиксирует лишь один элемент из М. Число 0 называют рангом нульместной операции.
О. Унарная операция на М – это отображение М в М или обычная одноместная функция, область определения которой совпадает с М. Унарной операции приписывают ранг 1 и называют также оператором.
Понятие алгебраической операции может быть определено для любого ранга n.
О. Пусть Мn есть n-ая степень непустого множества М. Отображение множества Мn в М называют n-местной алгебраической операцией или просто n-местной операцией на множестве М.
При n=3 операцию называют тернарной, но чаще всего рассматривают бинарные операции.
Если не для любого элемента из Мn существует образ в М, то операцию называют частичной. Например, вычитание во множестве натуральных чисел N является частичной операцией.
Бинарные операции могут обладать рядом свойств:
коммутативностью, ассоциативностью, сократимостью слева (справа) и просто сократимостью, дистрибутивностью одной операции относительно другой, существованием левого и правого нейтральных элементов, обозначаемых соответственно 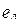 и
и 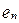 , а также просто нейтрального элемента е. Кроме того, если бинарная операция обладает нейтральным элементом еÎМ, то для любого элемента аÎМ могут существовать правый и левый симметричные к нему элементы, обозначаемыми соответственно а^ и ^а, и просто симметричный к нему
, а также просто нейтрального элемента е. Кроме того, если бинарная операция обладает нейтральным элементом еÎМ, то для любого элемента аÎМ могут существовать правый и левый симметричные к нему элементы, обозначаемыми соответственно а^ и ^а, и просто симметричный к нему 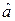 (могут быть и другие обозначения). Определения указанных свойств можно найти в [1] и [3].
(могут быть и другие обозначения). Определения указанных свойств можно найти в [1] и [3].
Операции могут обладать и некоторыми другими свойствами. Отметим некоторые из них.
О. Элемент 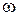 называется поглощающим слева (справа) относительно операции *, если для любого элемента хÎМ имеет место равенство
называется поглощающим слева (справа) относительно операции *, если для любого элемента хÎМ имеет место равенство 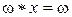 (
(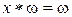 ), и поглощающим (аннулятором), если он поглощающий слева и справа.
), и поглощающим (аннулятором), если он поглощающий слева и справа.
О. Операция * называется идемпотентной, если для любого хÎМ 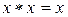 .
.
Упр. 1. Пусть М – непустое множество, Р(М) – множество всех его подмножеств, называемый его булеаном. Докажите, что операция нахождения разности на Р(М) не является ассоциативной.
Упр. 2. Докажите, что декартово умножение множеств дистрибутивно относительно разности.
Упр. 3. Докажите, что если для операции * существуют 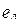 и
и 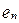 , то они совпадают, и для этой операции нет других нейтральных элементов.
, то они совпадают, и для этой операции нет других нейтральных элементов.
Упр. 4. Докажите, что если для операции * на множестве М существуют для элемента аÎМ симметричные элементы а^ и ^а, то они совпадают, и симметричный элемент для а единственный.
Упр. 5. Пусть задана операция * на множестве N такая, что 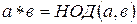 . Найдите поглощающий элемент. Является ли эта операция идемпотентной?
. Найдите поглощающий элемент. Является ли эта операция идемпотентной?
Аддитивная и мультипликативная формы записи операций. Чаще всего используются аддитивная и мультипликативная формы записи бинарной операции, называемые соответственно сложением и умножением и обозначаемыми знаками + и  (иногда вместо
(иногда вместо  используется и так называемый «немой» знак). Но наиболее распространенной является мультипликативная запись.
используется и так называемый «немой» знак). Но наиболее распространенной является мультипликативная запись.
В связи с этим изменяется и терминология понятий заданной операции, которую можно записать в виде следующей таблицы:
Операция общего вида 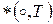
| умножение  или «немой» знак или «немой» знак
| сложение + |
| Результат операции | произведение | сумма |
| Нейтральный элемент | единичный элемент е 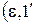 и т.п.) и т.п.)
| нулевой элемент 0 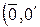 и т.п.) и т.п.)
|
Симметричный элемент для а (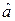 ) )
| обратный для а 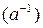
| противоположный для а (-а) |
Алгебры (алгебраические системы)
О. Алгеброй называется упорядоченная пара 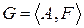 , где А – непустое множество и F – множество операций на А.
, где А – непустое множество и F – множество операций на А.
Множество А называется основным множеством алгебры G, а множество операций F – ее главными или внутренними операциями.
Мы будем рассматривать алгебры лишь с конечным числом операций. Поэтому алгебру G можно будет записать в виде 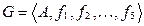 , где
, где 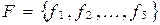 .
.
Если среди главных операций есть нульместные операции, например, 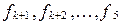 , фиксирующие соответственно элементы
, фиксирующие соответственно элементы 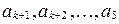 из А, то алгебру G можно записать в виде
из А, то алгебру G можно записать в виде 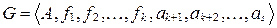 . При этом указанные выделенные элементы называются главными элементами алгебры G.
. При этом указанные выделенные элементы называются главными элементами алгебры G.
Мы будем рассматривать и алгебраические системы, состоящие из двух множеств и с определенными в них операциями нескольких видов, например, системы вида 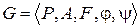 , где А – основное множество, Р – вспомогательное или дополнительное множество, обычно в качестве Р фигурирует некоторое числовое поле или даже коммутативное кольцо (определения их будут даны ниже), F – совокупность главных операций, определенных на А,
, где А – основное множество, Р – вспомогательное или дополнительное множество, обычно в качестве Р фигурирует некоторое числовое поле или даже коммутативное кольцо (определения их будут даны ниже), F – совокупность главных операций, определенных на А, 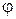 - отображение
- отображение 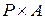 в А, а
в А, а 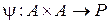 .
.
Приведем определения некоторых видов алгебр.
О. Алгебра 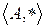 называется полугруппой, если операция
называется полугруппой, если операция 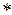 ассоциативна.
ассоциативна.
Обычно в полугруппах пользуются мультипликативной записью операции.
Если операция в полугруппе коммутативна, то полугруппу называют коммутативной.
О. Алгебра 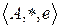 с бинарной операцией
с бинарной операцией 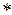 называется моноидом, если операция ассоциативна и существует нейтральный элемент е.
называется моноидом, если операция ассоциативна и существует нейтральный элемент е.
Очевидно, что любой моноид является полугруппой, но не любая полугруппа будет моноидом. Например, множество целых четных чисел относительно умножения является полугруппой, но не моноидом (проверьте!).
Важнейшими классами алгебр в курсе математики, включая и школьный курс, являются основные числовые системы. Их принято обозначать через 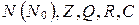 .
.
Упр. 6. Образует ли полугруппу множество всех иррациональных чисел относительно операции умножения.
Упр. 7. На множестве натуральных чисел N заданы операции 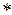 и
и 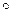 :
: 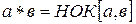 ,
, 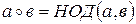 . Относительно какой операции множество N является моноидом и полугруппой?
. Относительно какой операции множество N является моноидом и полугруппой?
Упр. 8. На множестве Q задана операция 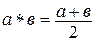 . Является ли Q полугруппой относительно этой операции?
. Является ли Q полугруппой относительно этой операции?
Наибольший интерес представляет класс алгебр, называемых группами, из-за их широкого применения как к самой математике, так и при решении задач прикладного характера.
Приведем два определения группы.
О.1. Непустое множество G с одной бинарной операцией 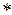 называется группой, если выполняются следующие условия:
называется группой, если выполняются следующие условия:
1) операция 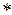 ассоциативна;
ассоциативна;
2) имеется нейтральный элемент;
3) для каждого элемента 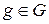 в G имеется симметричный элемент.
в G имеется симметричный элемент.
О.2. Непустое множество G с одной бинарной операцией 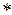 называется группой, если выполняются следующие условия:
называется группой, если выполняются следующие условия:
1) операция 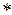 ассоциативна;
ассоциативна;
2) во множестве G для любых а и в разрешимы уравнения 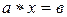 и
и 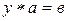 и каждое из них имеет одно решение.
и каждое из них имеет одно решение.
Существуют и другие определения группы, см., например, [3], стр. 94. Но все эти определения оказываются эквивалентными.
Докажем эквивалентность приведенных выше двух определений группы.
а) Пусть множество G является группой согласно первому определению. Покажем, что это множество является группой и согласно второму определению. Для этого достаточно проверить выполнимость условия 2) этого определения.
По предположению для 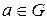 имеется в G симметричный для него элемент
имеется в G симметричный для него элемент 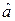 . Умножив на
. Умножив на 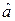 обе части уравнений
обе части уравнений 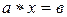 и
и 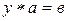 (первое слева, второе справа) и, воспользовавшись ассоциативностью операции, будем иметь
(первое слева, второе справа) и, воспользовавшись ассоциативностью операции, будем иметь 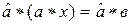 и
и 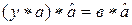 или
или 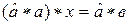 и
и 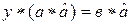 . Пусть
. Пусть 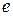 - нейтральный элемент группы G, тогда
- нейтральный элемент группы G, тогда 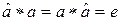 и
и 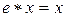 ,
, 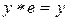 или
или 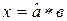 и
и 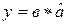 . Единственность решений указанных уравнений следует из определения алгебраической операции и единственности существования нейтрального и симметричного элементов.
. Единственность решений указанных уравнений следует из определения алгебраической операции и единственности существования нейтрального и симметричного элементов.
б) Пусть множество G является группой согласно второму определению. Покажем, что это множество будет группой и согласно первому определению.
Выполнимость ассоциативности операции гарантируется вторым определением. Покажем существование нейтрального элемента. Рассмотрим уравнение 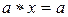 , где
, где 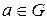 . Согласно второму определению оно разрешимо в G и имеет единственное решение, обозначим его через
. Согласно второму определению оно разрешимо в G и имеет единственное решение, обозначим его через 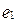 , т.е.
, т.е. 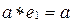 .
.
Проверим, что для любого 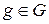
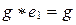 . Действительно, рассмотрим уравнение
. Действительно, рассмотрим уравнение 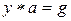 , которое в G разрешимо. Умножим обе части его на
, которое в G разрешимо. Умножим обе части его на 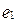 и, воспользовавшись ассоциативностью операции, будем иметь
и, воспользовавшись ассоциативностью операции, будем иметь 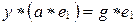 , но
, но 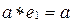 , т.е.
, т.е. 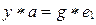 , или
, или 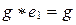 . Таким образом,
. Таким образом, 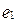 является правым нейтральным элементом.
является правым нейтральным элементом.
Аналогично доказывается существование левого нейтрального элемента 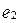 , исходя из разрешимости уравнения
, исходя из разрешимости уравнения 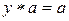 . Выше было показано, что
. Выше было показано, что 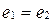 .
.
Докажем, что для элемента  из
из 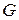 существует в
существует в  симметричный ему элемент
симметричный ему элемент 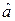 .
.
Рассмотрим уравнение 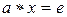 , где
, где 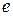 - нейтральный элемент группы
- нейтральный элемент группы 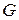 . Это уравнение по условию в
. Это уравнение по условию в 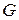 разрешимо, решение его обозначим через
разрешимо, решение его обозначим через 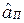 , т.е.
, т.е. 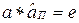 ,
, 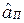 - правый симметричный для
- правый симметричный для  элемент. Аналогично проверяется существование левого нейтрального для
элемент. Аналогично проверяется существование левого нейтрального для  элемента
элемента 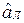 , исходя из разрешимости уравнения
, исходя из разрешимости уравнения 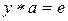 . Выше показано, что
. Выше показано, что 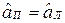 .
.
Эквивалентность двух определений группы доказана.
По определению групповая операция не обязана быть коммутативной. Если же операция в группе коммутативна, то ее называют коммутативной или абелевой, по имени выдающегося норвежского математика Н.Х. Абеля (1802-1829).
О. Число элементов группы 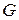 называют ее порядком и обозначают в виде
называют ее порядком и обозначают в виде 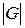 .
.
Если число элементов в группе конечно, то ее называют конечной, в противном случае – бесконечной.
В дальнейшем преимущественно будем пользоваться мультипликативной записью операции в группе, т.е. 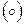 .
.
Примеры групп:
1. Множество целых чисел 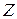 с операцией сложения. Выполнимость свойств группы легко проверяется. (Проверьте, что относительно операции умножения это множество не является группой)
с операцией сложения. Выполнимость свойств группы легко проверяется. (Проверьте, что относительно операции умножения это множество не является группой)
2. Рассмотрим множество всех взаимно однозначных отображений первых четырех натуральных чисел 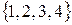 на себя. Такое отображение называют их подстановкой и обозначают
на себя. Такое отображение называют их подстановкой и обозначают 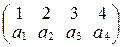 , где
, где 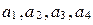 - это те же числа 1, 2, 3, 4, быть может, расположенные в другом порядке. Такую запись назовем стандартной записью подстановки. Так как отображение определяется однозначно указанием образа элемента, то одна и та же подстановка может быть записана разными способами, например, имеют место равенства:
- это те же числа 1, 2, 3, 4, быть может, расположенные в другом порядке. Такую запись назовем стандартной записью подстановки. Так как отображение определяется однозначно указанием образа элемента, то одна и та же подстановка может быть записана разными способами, например, имеют место равенства:
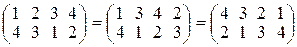 .
.
Множество всех таких подстановок обозначим через 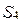 . Так как каждая подстановка может быть записана в стандартной форме, то их будем считать различными, если у них различны вторые строчки, которые представляют из себя перестановки из четырех чисел. Но число различных перестановок из четырех чисел равно
. Так как каждая подстановка может быть записана в стандартной форме, то их будем считать различными, если у них различны вторые строчки, которые представляют из себя перестановки из четырех чисел. Но число различных перестановок из четырех чисел равно 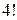 (четыре факториал) или
(четыре факториал) или 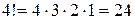 . В
. В 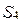 выделяют так называемую тождественную подстановку
выделяют так называемую тождественную подстановку 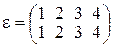 , она может быть записана в виде
, она может быть записана в виде 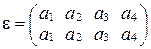 .
.
| <== previous lecture | | | next lecture ==> |
| Для нататок | | | Модель IS— LM |