Средние отклонения от средних величин
Date: 2015-10-07; view: 343.
Каждая статистическая величина от среднего значения отличается (отклоняется) по-разному и в любую сторону: со знаком плюс или минус. Поэтому для оценки типичности полученной средней величины надо знать величину среднего отклонения совокупности от нее. Поскольку неизбежны и отрицательные отдельные отклонения, необходима нейтрализация знака минус, иначе среднего отклонения не получится. Этого можно достичь двумя способами: принять отрицательные отклонения по модулю или возвести их во вторую степень (в квадрат).
При первом способе образуется среднее линейное отклонение, а при втором — среднее квадратическое. В связи с тем, что средние величины могут быть простыми и взвешенными, аналогичными могут быть и средние отклонения. Поэтому среднее линейное отклонение определяется по формулам
– простое; (1.22)
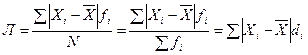– взвешенное. (1.23)
В этих формулах прямые скобки означают, что разности или отклонения берутся по модулю, то есть без учета знака. Если ошибочно вместо прямых скобок принять обычные круглые, то получится Л=0.
При использовании второго способа вначале определяется дисперсия отклонений по формулам
– простая; (1.24)
– взвешенная. (1.25)
Дисперсия альтернативного признака (т.е. имеющего две взаимоисключающие разновидности, например, пол человека – мужской или женский, качество продукции – годная или бракованная) определяется по формуле 1.25, если вместо Xi подставить 1 и 0 (так как признак может принимать только 2 значения). Зная, что:
p + q = 1,
где p – доля единиц, обладающих признаком, q – доля единиц не обладающих им.
Среднее значение можно найти по формуле (1.14):
.
Таким образом получим формулу дисперсии альтернативного признака, применив формулу (1.25):
.
Таким образом, дисперсия альтернативного признака равна
. (1.26)
Предельное значение дисперсии альтернативного признака равно 0,25; оно получается при p = q = 0,5.
В отличие от математики статистика оперирует не абстрактными, а смысловыми величинами, имеющими размерность. Поэтому и дисперсия здесь не безразмерная, как в математике, а сопровождается квадратической размерностью. Например, если статистическая величина измеряется в годах, или рублях, то дисперсия отклонений получится в «квадратных» годах или в «квадратных» рублях.
Для получения обычной размерности находится среднее квадратическое отклонение («сигма») как корень квадратный из дисперсии. То есть
= 
. (1.27)
Однако значения средних отклонений, как любой абсолютной величины, служат лишь количественной мерой анализа статистической совокупности. Для качественного анализа применяются относительные критерии, называемые коэффициентами вариации.
| <== previous lecture | | | next lecture ==> |
| Структурные средние | | | Коэффициенты вариации |