
Проверка ряда на наличие тренда
Date: 2015-10-07; view: 401.
Всякий ряд динамики теоретически может быть представлен в виде составляющих:
Ø тренд – основная тенденция развития ряда, обусловливающая увеличение или снижение его уровней;
Ø циклические (периодические) колебания (в том числе сезонные);
Ø случайные колебания.
Проверка ряда динамики на наличие в нем тренда возможна несколькими способами (в порядке усложнения):
1. Графический метод, когда на графике по оси абсцисс откладывается время, а по оси ординат – уровни ряда. Соединив полученные точки линиями, в большинстве случаев можно выявить тренд визуально.
2. Метод средних, согласно которому изучаемый ряд динамики делится на два равных подряда, для каждого из которых определяется средняя величина  и
и  . И если они различаются существенно (более 10%), то признается наличие тренда.
. И если они различаются существенно (более 10%), то признается наличие тренда.
3. Метод Кокса и Стюарта, согласно которому ряд динамики делится на три равные по числу уровней группы и существенное различие выявляется между средними уровнями первой и третьей групп. Если общее число уровней не делится на три, то надо добавить недостающий уровень или исключить излишний.
4. Метод Валлиса и Мура, согласно которому наличие тренда признается в том случае, если ряд не содержит либо содержит в приемлемом количестве фазы, т.е. перемену знака при определении абсолютного изменения цепным способом.
5. Метод серий, согласно которому каждый уровень ряда считается принадлежащим к одному из двух типов, например типу А – меньше медианного или среднего значения или типу В – больше его. Затем в образовавшейся последовательности типов устанавливается число серий R. Они называются последовательностью уровней одинакового типа, которая граничит с уровнями другого типа. Если в ряду динамики общая тенденция к росту или снижению уровней отсутствует, то число серий является случайной величиной, распределенной приближенно по нормальному закону (при n>30) или по распределению Стьюдента (при n<30). Следовательно, если закономерности в изменениях уровней нет, то случайная величина R оказывается в доверительном интервале

где t – коэффициент доверия для принятого уровня вероятности при нормальном законе или со степенью свободы k = (n - 1) при распределении Стьюдента;
 – среднее число серий в ряду, определяемое по формуле:
– среднее число серий в ряду, определяемое по формуле: 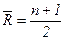 ;
;  – среднее квадратическое отклонение числа серий в ряду, определяемое по формуле
– среднее квадратическое отклонение числа серий в ряду, определяемое по формуле 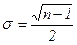 .
.
Подставляя среднее число серий и его среднее квадратическое отклонение в доверительный интервал, получим его развернутое значение в виде
 .
.
Значит, с заданной вероятностью тренд имеет место, если установленное число серий ряда не входит в доверительный интервал, и тренд отсутствует, если установленное число серий находится в этом интервале.
| <== previous lecture | | | next lecture ==> |
| Средний уровень ряда и средние изменения | | | Непосредственное выделение тренда |