
Preparation Strategies
Date: 2015-10-07; view: 465.
Вариант №33
Вариант №32
Вариант №31
Вариант №30
Вариант №29
Вариант №28
Вариант №27
Вариант №26
Вариант №25
Вариант №24
Вариант №23
Вариант №22
Вариант №21
Вариант №20
Вариант №19
Вариант №18
Вариант №17
Вариант №16
Вариант №15
Вариант №14
Вариант №13
Вариант №12
Вариант №11
Вариант №10
Вариант №9
Вариант №8
Вариант №7
Вариант №6
Вариант №5
Вариант №4
Вариант №3
Вариант №2
Вариант №1
Приложение Литература для дальнейшего чтения
Вал,
ДЗЕН СЕГОДНЯ
ТЕМА
• Маркетинг полон парадоксов и противоречий. Дзен учит, что решение позволяет найти не рациональность, а отражение.
• Главная обязанность маркетолога состоит в том, чтобы расшевелить, заставить бурлить рынок и найти минутку для дзен.
PS
Надеюсь, тебе понравилась прогулка по малоизученным уголкам маркетинга. По сути своей маркетинг – очень серьезное занятие, но иногда он бывает довольно забавным. Он выводит организацию на тропинку, ведущую к цели. Большинство промышленных компаний стремятся к получению краткосрочной прибыли и увеличению марочного капитала, цели общественных организаций заключаются в привлечении новых членов и удовлетворении нужд потребителей, Маркетинг занимается серьезными вопросами, что делает его увлекательным и интересным. Приятно иметь дело и с самими маркетологами. Они помешаны на классификациях, понимая, что потребности каждого из нас различны. Заслуги некоторых из маркетологов высоко оценены в самых известных университетах, другие с трудом получили среднее образование. Одни – излишне рациональны, другие – хватаются за любые безумные идеи. Если между ними и существует какая-то связующая нить, то это только глубокое понимание окружающего мира. Они научились управлять волнами моды, но не они их инициируют,
Всего хорошего, я надеюсь, ты не разочаруешься в своих новых обязанностях. Наслаждайся ими.
В течение тридцати лет основным учебником по маркетингу является книга Филипа Котлера «Маркетинговое менеджмент» (Marketing Management by Philip Kotler)1. Девятое ее издание насчитывает свыше 800 страниц, на которых вы найдете все, что вы хотите знать о маркетинге в его неоклассической версии. Чтение объемного фолианта требует времени, но ценность содержащейся в нем информации несомненна. Филип Котлер навел порядок и поддерживает дисциплину в каждом разделе маркетинга.
Конкуренцию ему может составить разве что поразительно ясный и глубокий учебник Питера Дойля «Менеджмент: стратегия и тактика» (Marketing Management and Strategy by Piter Doyle)2.
А вот еще несколько серьезных книг.
Книга Глена Урбана «Введение в маркетинговые стратегии» (Advanced Marketing Strategy: phenomena, analysis and decisions by Glen Urban. – Prentice Hall, 1991) требует немалых интеллектуальных усилий, ориентирована на серьезных аналитиков.
Проблемам промышленного маркетинга и маркетинга услуг посвящены работы Кристофера Лавлока «Управление в сфере услуг» (Christopher Lovelock's Managing Services. – Prentice Hall, 1992) и Томаса Спеха «Маркетинговое управление в бизнесе» (Tomas Speh's Business Marketing Management. – Dryden Pressi, 1985).
Проблемам международного маркетинга посвящено множество учебников. Среди них выделяется труд французского специалиста Жана-Клода Узуниера «Международный маркетинг» (International Marketing by Jean-Claude Usunier. – Prentice Hall, 1993). Большинство других принадлежат перу американских авторов, которые, кажется, пытаются преодолеть свой этноцентризм.
Конфликтная парадигма (или стратегия) маркетинга кратко изложена в классической работе Майкла Портера «Конкурентные стратегии» (Michael Porter's Competitive Strategy. – The Free Press, 1980).
1 Magid M. Abraham and Leonard M. Lodish, «Gettingthe most of advertising and promotion», Harvard Business Review (May–June 1990).
1 Philip Kotler, Marketing Management. Analysis, planning, implemention and control.
1 Karl von Clausewitz, On War (London, Penguin Classics, 1982).
2 Al Ries and Jack Trout, Marketing Warfare (Singapore, McGraw Hill, 1986).
1 John Kay, Foundations of Corporate Success (Oxford Uniiversity Press, 1993).
1 Selected works of Мао Tse Tung, vol.1, chapter V (Peking, Foreign Languages Press,1967).
2 Karl von Clansewitz, On War, p. 396.
1 Selected works of Мао Tse Tung, p. 249.
1 Selected works of Мао Tse Tung, p. 215
1 Philip Kotler, Marketing Management. (Englewood Cliffs, NJ, Prentice-Hall, 1991), p. 4.
1 Gavin Barret, Forensic Marketing (London, McGraw-Hill, 1994), p. 1.
1 Adam Smith, Wealth of Nations.
1 Gene M. Grossman and Elhanan Helpman, innovation and Growth in The Global Economy (MIT Press, 1991).
1 Datamonitor, Marketing (July 13, 1995).
1 Michael D. Hutt and Thomas W. Speh, Business Marketing Management (New York, The Dry den Press, 1989).
2 «The Service Area in a Fog», The Economist (London, May 23, 1987).
1 Al Ries and Jack Trout, Positioning: The Battle for your Mind, (New York.McGraw-Hill, 1986).
1 Dennis W. Rook «Researching Consumer Fantasy», Research in Consumer Behavior,vol. 3, (1988) p. 247-270.
Sidney J. Levy «Dreams, Fairy Tales, Animals and Cars», Psychology & Marketing,
vol. 2, no. 2, (1985) p. 67-81.
1 Al Ries and Jack Trout, Marketing Warfare, (New York, McGraw-Hill, 1986).
1 В России этот рынок находится в стадии формирования, порой носит полукриминальный характер. Тем не менее многие компании ведут собственные базы данных, отдельные программные продукты имеются как в открытой продаже, так и на «черном рынке». Чаще всего эти базы используются для почтовой рассылки, но распространение телефонных продаж, вероятно, не минует и нас. – Прим. ред.
2 К сожалению, пока в России такие посреднические фирмы только начали заявлять о себе. Рыночная экономика развивается на основе широкого разделения труда. Посреднические торговые фирмы, берущие заказы на реализацию от нескольких производителей и перепродающие товары непосредственным потребителям или розничным торговцам, стимулируют развитие производства, особенно малого бизнеса (малые предприятия, семейные фирмы, кооперативы и пр.). – Прим. ред.
1 London Business School Ph D, 1994.
1 Frank McKenna «It won't happen to me: Unrealistic optimism or illusion of control», British Journal of Psychology (1993),84, 39-50.
1 Brand development: Toward a process model of extension decisions. Tim Ambler and Chrris Styles, published working paper, London Business School, 1994.
1 A series of Guidance to Good Practice leaflets (1986).
1 А.P. de Gens, «Planningas Lerning», Harvard Business Review Mar–Apr. 1988.
1 C.Argyris, On Organizational Learning, Cambridge, Blackwell Business, 1993.
1 Ted Levitt, «After the sale is over», Harvard Business Review (Sept.–Oct. 1983).
1 Henley Centre,Teleculture 2000 (1995).
2 Christian Gronroos, «Relationship Approach to Marketing in Service Contexts: The Marketing and Organisational Behaviour Interface», Journal of Business research 20 (1990), p. 3-11.
Evert Gummeson, «The New Marketing – Developing Long-term Interactive Re-latioships»,Long Range Planning 20 (1987), p. 4,10-20. Evert Gummeson, «Relationship Marketing – A New Way of Doing Business», European Business Report 30,(Autumnl993), p. 52-56. H.Hakansson, Interactional Marketing and Purchasing of Industrial Goods: An Interaction Approach (New York: Wiley, 1982).
1 Leonard L. Berry, Relationship Marketing, in Emerging Perspectives on Services Marketing, L.L., Berry et al. eds (Chicago, American Marketing Association, 1983), p.25-28.
Hans B. Thorelli, «Political Science and Marketing» in Theory in Marketing, R. Cox, W. Anderson and S.J. Shapiro eds (Homewood, IL, Richard D.Irwin, Inc., 1964), p.125-36.
Hans B. Thorelli, «Networks: Between Markets and Hierarchies», Strategic Management Journal, vol. 7 (1986), p. 37-51.
2 Johan Arndt, «The political economy Paradigm: Foundation for Theory Building in Marketing», Jornal of Marketing (Fall 1983), p. 44-54.
3 James С. Anderson and James A. Narns, «Partnering as a Focused Market Strategy». California Management Review 33 (Spring 1991), p. 95-113.
4 R.H. Coflse,«The Nature of the Firm»,Economica NS4 (1937), p. 386-405. Oliver Williamson, The Economic Institutions of Capitalism (New York and London, The Free Press, 1985).
Oliver Williamson, Discussion of 'Breachof Trust in Hostile Takeovers'in Corporate Takeovers: Causes and Consequences, Alan Auerbach, ed. (Chicago, University of Chicago Press, 1988).
5 Kurt Salmon Associates Inc., Efficient Consumer Response: Enhancing Consumer Value in the Grocery Industry (Washington, Food Marketing Institute, 1993).
1 Martin Christopher, Adrian Payne and David Ballantyne, Relationship Marketing. Bringing quality, customer service and marketing together (Oxford, Butterworth-Heinemann Ltd., 1991).
Jagdish N. Sheth and Atui Parvatiyar (eds), Research Conference Proceedings, Relationship Marketing: Theory, Methods and Applications, June 11-13 (Atlanta, Centre for Relashionshi p Marketing, Emory University, 1994).
2 Tim Ambler, «The Relational Paradigm: A Synthesis», in Jagdish N.Sheth and Atui Parvatiyar (eds), Research Conference Proceedings, Relationship Marketing: Theory, Methods and Applications, June 11-13, (Atlanta; Centre for Relationship Marketing, Emory University, 1994).
David T. Wilson and Kristan K.E. Matter,Buyer-Seller Relationships. Alternative Conceptualizations». New Perspectives on International Marketing, Stanley J. Paliwoda (ed.) (London, Routledge, 1991) chapter 5, p. 87.
3 Наиболее известный и самый популярный в бизнес-школах учебник, автор которого является приверженцем неоклассической парадигмы, принадлежит перу Филипа Котлера. Philip Kotler, Marketing Management: Analysis, Planning, Implementation and Control, 8th edition (Englewood Cliffs, NJ, Prentice-Hall, 1993).
1 Henry Mintzberg, «The Fall and Rise of Strategic Planning» Harvard Business Review (Jan.- Feb. 1994).
Henry Mintzberg and James B. Quinn, The Strategy Process (Englewood Cliffs, NJ, Prentice-Hall International, 1991).
Michael E. Porter, Competition in Global Industries (Harvard Business School Press, 1986) Michael E. Porter, Competitive Strategy (New York Free Press, 1980).
1 Philip Kotler, <i'Ftom Transations to Relashionshi ps»,MSI Review (Spring 1991).
1 Вradley T. Gale, Managing Customer Value (New York, The Free Press, 1994). Robert Jacobson and David A. Aaker, «The Strategic Role of Product Quality», Jornal of Marketing 51 (October 1987), p. 31-44.
Ram Narasimhan, Soumen Gosh and David Mendez, «A Dynamic Model of Product Quality and Pricing Decisions on Sales Response». Desision Sciences 24(5) (1993), p.893-908.
Lynn Phillips, Dae R. Chunget and Robert D. Buzzel, «Product Quality, Cost Position and Business Performance A Test of Some Hypotheses», Jornal of Marketing 47 (Spring 1983), p. 26-43.
1 Marketing (Aug 3, 1996), p. 19.
1 The Marketing Society Review, (Summer 1995).
1 На русском языке существуют три издания этой книги. Первая называлась «Управление маркетингом», вторая – «Основы маркетинга». Третья – то самое девятое издание, о котором говорит Тим Амблер, – выпущена издательством «Питер Ком» в 1998 г. под названием «Маркетинг менеджмент». – Прим. ред.
2 Этот учебник получил приз «Лучшая книга по менеджменту в Европе». Второе издание этой книги вышло на русском языке практически одновременно с ее английским оригиналом. См.: Питер Дойль «Менеджмент: стратегия и тактика». – СПб.: Питер Ком, 1999. – Прим. ред.
1. Вычислить определитель: 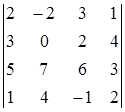 .
.
2. Найти АВ–ВА, где: 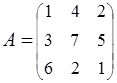 ;
; 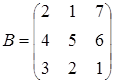 .
.
3. Найти А-1, где: 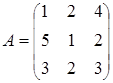 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ=  матричным способом.
матричным способом.
4. Решить систему а) методом Крамера; б) методом Гаусса:
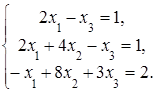 Сделать проверку.
Сделать проверку.
5. Три стороны треугольника АВС заданы уравнениями: (АВ): х-3у–23=0; (ВС): 7х+9у+19=0; (АС): 4х+3у+13=0. Составить уравнение высоты, проведенной из вершины В и уравнение медианы, проведенной из вершины А.
6. Линия задана уравнением r=r(φ) в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от φ=0 до φ=2π и придавая φ значения через промежуток π/8; 2) найти уравнение данной линии в прямоугольной декартовой системе координат, у которой начало совпадает с полюсом, а положительная ось абсцисс – с полярной осью; 3) по полученному уравнению определить, какая это линия.
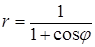 .
.
7. Даны координаты вершин пирамиды  .
.
Найти: 1) длину ребра  ; 2) угол между ребрами
; 2) угол между ребрами  и
и 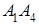 ; 3) угол между ребром
; 3) угол между ребром 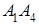 и гранью
и гранью  ; 4) площадь грани
; 4) площадь грани  ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж.
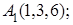
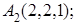
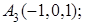
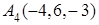 .
.
8. Найти точку В, симметричную точке А(1, 3, –4) относительно плоскости 3х+у–2z=0.
1. Вычислить определитель: 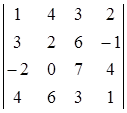 .
.
2. Найти АВ–ВА, где: 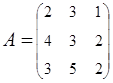 ;
; 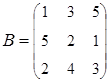 .
.
3. Найти А–1, где: 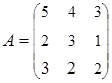 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ=  матричным способом.
матричным способом.
4. Решить систему а) методом Крамера; б) методом Гаусса:
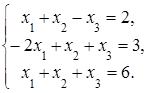 Сделать проверку.
Сделать проверку.
5. Даны уравнения одной из сторон ромба 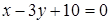 и одной из его диагоналей
и одной из его диагоналей 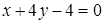 ; диагонали ромба пересекаются в точке
; диагонали ромба пересекаются в точке 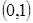 .
.
Найти уравнения остальных сторон ромба.
6. Линия задана уравнением r=r(φ) в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от φ=0 до φ=2π и придавая φ значения через промежуток π/8; 2) найти уравнение данной линии в прямоугольной декартовой системе координат, у которой начало совпадает с полюсом, а положительная ось абсцисс – с полярной осью; 3) по полученному уравнению определить, какая это линия.
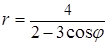 .
.
7. Даны координаты вершин пирамиды 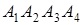 .
.
Найти: 1) длину ребра 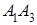 ; 2) угол между ребрами
; 2) угол между ребрами  и
и 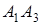 ; 3) угол между ребром
; 3) угол между ребром 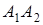 и гранью
и гранью 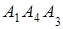 ; 4) площадь грани
; 4) площадь грани 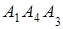 ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж.
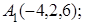
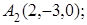
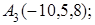
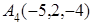 .
.
8. Найти точку М, симметричную точке N(1, 3, 5) относительно плоскости 2х–у–3z+5=0.
1. Вычислить определитель: 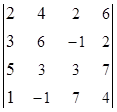 .
.
2. Найти АВ–ВА, где: 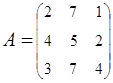 ;
; 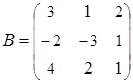 .
.
3. Найти А–1, где: 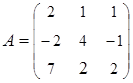 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ=  матричным способом.
матричным способом.
4. Решить систему а) методом Крамера; б) методом Гаусса:
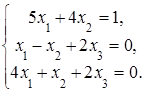 Сделать проверку.
Сделать проверку.
5. Даны две вершины 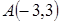 и
и 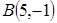 и точка
и точка 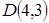 пересечения высот треугольника. Составить уравнения его сторон.
пересечения высот треугольника. Составить уравнения его сторон.
6. Линия задана уравнением r=r(φ) в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от φ=0 до φ=2π и придавая φ значения через промежуток π/8; 2) найти уравнение данной линии в прямоугольной декартовой системе координат, у которой начало совпадает с полюсом, а положительная ось абсцисс – с полярной осью; 3) по полученному уравнению определить, какая это линия.
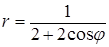 .
.
7. Даны координаты вершин пирамиды  .
.
Найти: 1) длину ребра 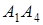 ; 2) угол между ребрами
; 2) угол между ребрами  и
и 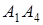 ; 3) угол между ребром
; 3) угол между ребром 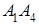 и гранью
и гранью  ; 4) площадь грани
; 4) площадь грани  ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж.
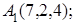
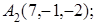
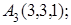
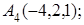
8. Найти проекцию точки Р(2, –5,7) на прямую, проходящую через точки М1(4, 5, 6) и М2(–2, –17, –8).
1. Вычислить определитель: 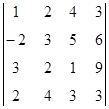 .
.
2. Найти АВ–ВА, где: 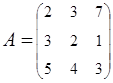 ;
; 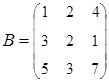 .
.
3. Найти А–1, где: 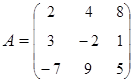 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ=  матричным способом.
матричным способом.
4. Решить систему а) методом Крамера; б) методом Гаусса:
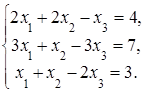 Сделать проверку.
Сделать проверку.
5. Уравнения двух сторон параллелограмма 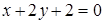 и
и 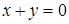 , а уравнение одной из его диагоналей
, а уравнение одной из его диагоналей 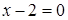 .Найти координаты вершин параллелограмма.
.Найти координаты вершин параллелограмма.
6. Линия задана уравнением r=r(φ) в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от φ=0 до φ=2π и придавая φ значения через промежуток π/8; 2) найти уравнение данной линии в прямоугольной декартовой системе координат, у которой начало совпадает с полюсом, а положительная ось абсцисс – с полярной осью; 3) по полученному уравнению определить, какая это линия.
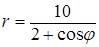 .
.
7. Даны координаты вершин пирамиды  .
.
Найти: 1) длину ребра 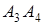 ; 2) угол между ребрами
; 2) угол между ребрами  и
и 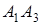 ; 3) угол между ребром
; 3) угол между ребром 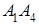 и гранью
и гранью  ; 4) площадь грани
; 4) площадь грани 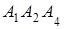 ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж.
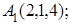
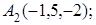
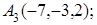
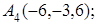
8. Найти точку Q, симметричную точке Р(4, 1, 6) относительно прямой
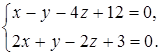
1. Вычислить определитель: 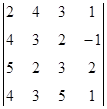 .
.
2. Найти АВ–ВА, где: 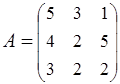 ;
; 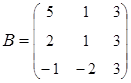 .
.
3. Найти А–1, где: 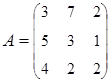 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ=  матричным способом.
матричным способом.
4. Решить систему а) методом Крамера; б) методом Гаусса:
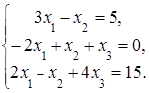 Сделать проверку.
Сделать проверку.
5. Три стороны треугольника 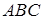 заданы уравнениями
заданы уравнениями 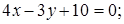
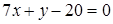 и
и 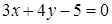 . Написать уравнение высоты и биссектрисы, проведенных из вершины
. Написать уравнение высоты и биссектрисы, проведенных из вершины 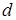 .
.
6. Линия задана уравнением r=r(φ) в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от φ=0 до φ=2π и придавая φ значения через промежуток π/8; 2) найти уравнение данной линии в прямоугольной декартовой системе координат, у которой начало совпадает с полюсом, а положительная ось абсцисс – с полярной осью; 3) по полученному уравнению определить, какая это линия.
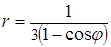 .
.
7. Даны координаты вершин пирамиды  .
.
Найти: 1) длину ребра 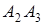 ; 2) угол между ребрами
; 2) угол между ребрами 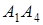 и
и 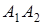 ; 3) угол между ребром
; 3) угол между ребром 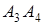 и гранью
и гранью  ; 4) площадь грани
; 4) площадь грани  ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж.
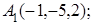
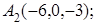
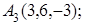
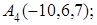
8. Найти точку Q, симметричную точке Р(2, –5, 7) относительно прямой
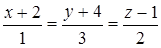
1. Вычислить определитель: 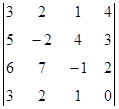 .
.
2. Найти АВ–ВА, где: 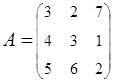 ;
; 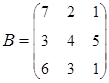 .
.
3. Найти А–1, где: 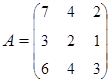 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ=  матричным способом.
матричным способом.
4. Решить систему а) методом Крамера; б) методом Гаусса:
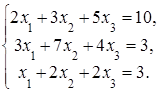 Сделать проверку.
Сделать проверку.
5. Даны вершины 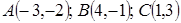 трапеции
трапеции 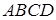
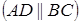 . Известно, что диагонали трапеции взаимно перпендикулярны. Найти координаты вершины
. Известно, что диагонали трапеции взаимно перпендикулярны. Найти координаты вершины 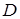 этой трапеции.
этой трапеции.
6. Линия задана уравнением r=r(φ) в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от φ=0 до φ=2π и придавая φ значения через промежуток π/8; 2) найти уравнение данной линии в прямоугольной декартовой системе координат, у которой начало совпадает с полюсом, а положительная ось абсцисс – с полярной осью; 3) по полученному уравнению определить, какая это линия.
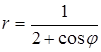 .
.
7. Даны координаты вершин пирамиды  .
.
Найти: 1) длину ребра 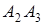 ; 2) угол между ребрами
; 2) угол между ребрами 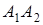 и
и 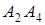 ; 3) угол между ребром
; 3) угол между ребром 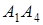 и гранью
и гранью 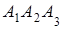 ; 4) площадь грани
; 4) площадь грани  ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж.
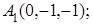
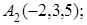
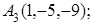
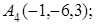
8. Найти проекцию точки А(2, 0, 3) на прямую 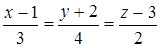 .
.
1. Вычислить определитель: 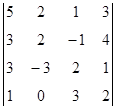 .
.
2. Найти АВ–ВА, где: 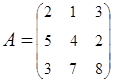 ;
; 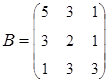 .
.
3. Найти А–1, где: 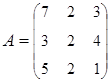 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ=  матричным способом.
матричным способом.
4. Решить систему а) методом Крамера; б) методом Гаусса:
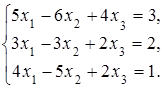 Сделать проверку.
Сделать проверку.
5. Даны уравнения двух сторон треугольника 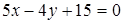 и
и 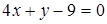 . Его медианы пересекаются в точке
. Его медианы пересекаются в точке 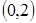 .Составить уравнение третьей стороны треугольника.
.Составить уравнение третьей стороны треугольника.
6. Линия задана уравнением r=r(φ) в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от φ=0 до φ=2π и придавая φ значения через промежуток π/8; 2) найти уравнение данной линии в прямоугольной декартовой системе координат, у которой начало совпадает с полюсом, а положительная ось абсцисс – с полярной осью; 3) по полученному уравнению определить, какая это линия.
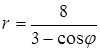 .
.
7. Даны координаты вершин пирамиды  .
.
Найти: 1) длину ребра 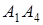 ; 2) угол между ребрами
; 2) угол между ребрами 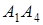 и
и 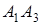 ; 3) угол между ребром
; 3) угол между ребром 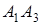 и гранью
и гранью 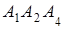 ; 4) площадь грани
; 4) площадь грани 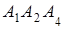 ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж.
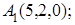
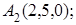
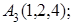
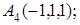
8. Найти проекцию точки А(1, –1, 2) на плоскость х+у+2z–3=0.
1. Вычислить определитель: 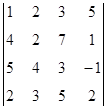 .
.
2. Найти АВ–ВА, где: 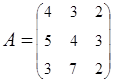 ;
; 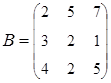 .
.
3. Найти А–1, где: 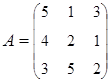 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ=  матричным способом.
матричным способом.
4. Решить систему а) методом Крамера; б) методом Гаусса:
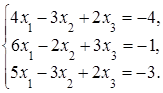 Сделать проверку.
Сделать проверку.
5. Даны две вершины 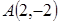 и
и 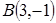 и точка
и точка 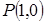 пересечения медиан треугольника
пересечения медиан треугольника 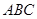 . Составить уравнение высоты треугольника, проведенной через третью вершину С.
. Составить уравнение высоты треугольника, проведенной через третью вершину С.
6. Линия задана уравнением r=r(φ) в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от φ=0 до φ=2π и придавая φ значения через промежуток π/8; 2) найти уравнение данной линии в прямоугольной декартовой системе координат, у которой начало совпадает с полюсом, а положительная ось абсцисс – с полярной осью; 3) по полученному уравнению определить, какая это линия.
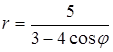 .
.
7. Даны координаты вершин пирамиды  .
.
Найти: 1) длину ребра  ; 2) угол между ребрами
; 2) угол между ребрами  и
и 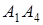 ; 3) угол между ребром
; 3) угол между ребром 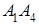 и гранью
и гранью  ; 4) площадь грани
; 4) площадь грани  ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж.

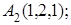
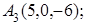
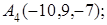
8. Найти проекцию точки М(0, –3, –2) на прямую 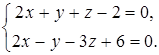
1. Вычислить определитель: 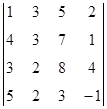 .
.
2. Найти АВ–ВА, где: 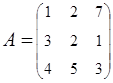 ;
; 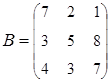 .
.
3. Найти А–1, где: 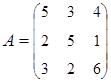 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ=  матричным способом.
матричным способом.
4. Решить систему а) методом Крамера; б) методом Гаусса:
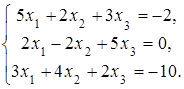 Сделать проверку.
Сделать проверку.
5. Уравнения двух высот треугольника 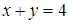 и
и 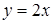 , и одна из его вершин А(0;2). Составить уравнение сторон треугольника.
, и одна из его вершин А(0;2). Составить уравнение сторон треугольника.
6. Линия задана уравнением r=r(φ) в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от φ=0 до φ=2π и придавая φ значения через промежуток π/8; 2) найти уравнение данной линии в прямоугольной декартовой системе координат, у которой начало совпадает с полюсом, а положительная ось абсцисс – с полярной осью; 3) по полученному уравнению определить, какая это линия.
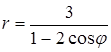 .
.
7. Даны координаты вершин пирамиды  .
.
Найти: 1) длину ребра 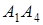 ; 2) угол между ребрами
; 2) угол между ребрами 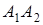 и
и 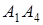 ; 3) угол между ребром
; 3) угол между ребром 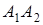 и гранью
и гранью 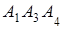 ; 4) площадь грани
; 4) площадь грани 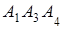 ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж.
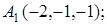
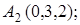
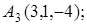
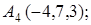
8. Найти проекцию точки М(3, 3, 3) на прямую 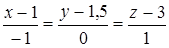 .
.
1. Вычислить определитель: 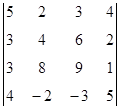 .
.
2. Найти АВ–ВА, где: 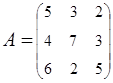 ;
; 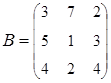 .
.
3. Найти А–1, где: 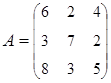 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ=  матричным способом.
матричным способом.
4. Решить систему а) методом Крамера; б) методом Гаусса:
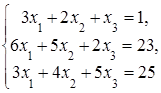 Сделать проверку.
Сделать проверку.
5. Даны уравнения двух медиан треугольника 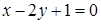 и
и 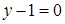 и одна из его вершин (1;3). Составить уравнения его сторон.
и одна из его вершин (1;3). Составить уравнения его сторон.
6. Линия задана уравнением r=r(φ) в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от φ=0 до φ=2π и придавая φ значения через промежуток π/8; 2) найти уравнение данной линии в прямоугольной декартовой системе координат, у которой начало совпадает с полюсом, а положительная ось абсцисс – с полярной осью; 3) по полученному уравнению определить, какая это линия.
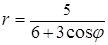 .
.
7. Даны координаты вершин пирамиды  .
.
Найти: 1) длину ребра 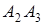 ; 2) угол между ребрами
; 2) угол между ребрами  и
и 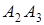 ; 3) угол между ребром
; 3) угол между ребром 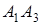 и гранью
и гранью 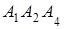 ; 4) площадь грани
; 4) площадь грани 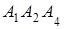 ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж.
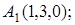
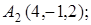
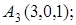
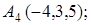
8. Найти точку К, симметричную точке М(1, 0, –1) относительно плоскости 2у+4z–1=0.
1. Вычислить определитель: 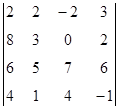 .
.
2. Найти АВ–ВА, где: 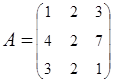 ;
; 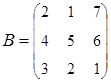 .
.
3. Найти А–1, где: 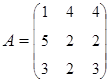 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ=  матричным способом.
матричным способом.
4. Решить систему а) методом Крамера; б) методом Гаусса:
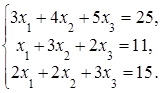 Сделать проверку.
Сделать проверку.
5. Две стороны треугольника заданы уравнениями 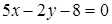 и
и 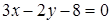 , а середина третьей стороны совпадает с началом координат. Составить уравнение этой стороны.
, а середина третьей стороны совпадает с началом координат. Составить уравнение этой стороны.
6. Линия задана уравнением r=r(φ) в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от φ=0 до φ=2π и придавая φ значения через промежуток π/8; 2) найти уравнение данной линии в прямоугольной декартовой системе координат, у которой начало совпадает с полюсом, а положительная ось абсцисс – с полярной осью; 3) по полученному уравнению определить, какая это линия.
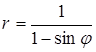 .
.
7. Даны координаты вершин пирамиды  .
.
Найти: 1) длину ребра 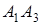 ; 2) угол между ребрами
; 2) угол между ребрами  и
и 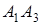 ; 3) угол между ребром
; 3) угол между ребром 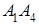 и гранью
и гранью  ; 4) площадь грани
; 4) площадь грани  ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж.
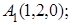
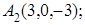
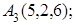
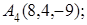
8. Найти проекцию точки М(–1, 0, –1) на плоскость 2х+6у–2z+11=0.
1. Вычислить определитель: 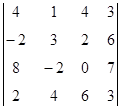 .
.
2. Найти АВ–ВА, где: 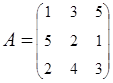 ;
; 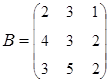 .
.
3. Найти А–1, где: 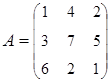 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ=  матричным способом.
матричным способом.
4. Решить систему а) методом Крамера; б) методом Гаусса:
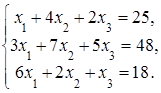 Сделать проверку.
Сделать проверку.
5. В треугольнике 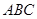 даны вершины
даны вершины 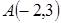 и
и 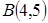 и точка пересечения медиан
и точка пересечения медиан 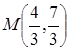 .Составить уравнение биссектрисы
.Составить уравнение биссектрисы 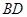 .
.
6. Линия задана уравнением r=r(φ) в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от φ=0 до φ=2π и придавая φ значения через промежуток π/8; 2) найти уравнение данной линии в прямоугольной декартовой системе координат, у которой начало совпадает с полюсом, а положительная ось абсцисс – с полярной осью; 3) по полученному уравнению определить, какая это линия.
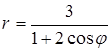 .
.
7. Даны координаты вершин пирамиды  .
.
Найти: 1) длину ребра 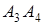 ; 2) угол между ребрами
; 2) угол между ребрами 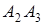 и
и 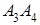 ; 3) угол между ребром
; 3) угол между ребром 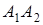 и гранью
и гранью 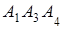 ; 4) площадь грани
; 4) площадь грани 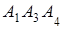 ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж. 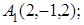
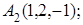
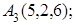
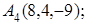
8. Найти проекцию точки М(1, 1, 1) на прямую 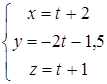
1. Вычислить определитель: 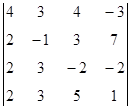 .
.
2. Найти АВ–ВА, где: 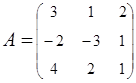 ;
; 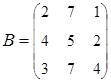 .
.
3. Найти А–1, где: 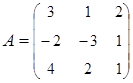 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ=  матричным способом.
матричным способом.
4. Решить систему а) методом Крамера; б) методом Гаусса:
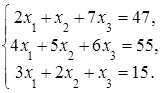 Сделать проверку.
Сделать проверку.
5. В треугольнике 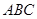 даны уравнения двух сторон
даны уравнения двух сторон 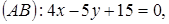
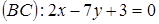 и медианы
и медианы 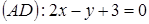 . Найти уравнение высоты
. Найти уравнение высоты 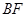 .
.
6. Линия задана уравнением r=r(φ) в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от φ=0 до φ=2π и придавая φ значения через промежуток π/8; 2) найти уравнение данной линии в прямоугольной декартовой системе координат, у которой начало совпадает с полюсом, а положительная ось абсцисс – с полярной осью; 3) по полученному уравнению определить, какая это линия.
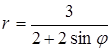 .
.
7. Даны координаты вершин пирамиды  .
.
Найти: 1) длину ребра 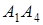 ; 2) угол между ребрами
; 2) угол между ребрами  и
и 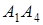 ; 3) угол между ребром
; 3) угол между ребром 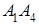 и гранью
и гранью  ; 4) площадь грани
; 4) площадь грани  ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж.
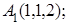
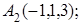
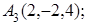
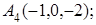
8. Найти точку Q, симметричную точке Р(0, 2, 1) относительно плоскости 2х+4у–3=0.
1. Вычислить определитель: 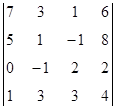 .
.
2. Найти АВ–ВА, где: 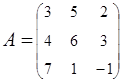 ;
; 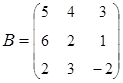 .
.
3. Найти А–1, где: 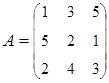 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ=  матричным способом.
матричным способом.
4. Решить систему а) методом Крамера; б) методом Гаусса:
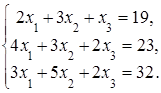 Сделать проверку.
Сделать проверку.
5. Даны уравнения двух высот треугольника 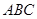 :
: 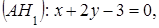
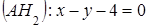 и абсциссы двух вершин
и абсциссы двух вершин 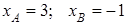 . Найти уравнения сторон и угол
. Найти уравнения сторон и угол  .
.
6. Линия задана уравнением r=r(φ) в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от φ=0 до φ=2π и придавая φ значения через промежуток π/8; 2) найти уравнение данной линии в прямоугольной декартовой системе координат, у которой начало совпадает с полюсом, а положительная ось абсцисс – с полярной осью; 3) по полученному уравнению определить, какая это линия.
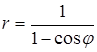 .
.
7. Даны координаты вершин пирамиды  .
.
Найти: 1) длину ребра 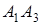 ; 2) угол между ребрами
; 2) угол между ребрами 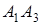 и
и 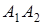 ; 3) угол между ребром
; 3) угол между ребром 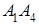 и гранью
и гранью  ; 4) площадь грани
; 4) площадь грани  ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж.
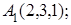
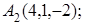
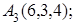
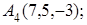
8. Найти проекцию точки М(1, 2, 3) на прямую 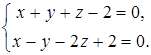
1. Вычислить определитель: 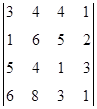 .
.
2. Найти АВ–ВА, где: 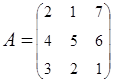 ;
; 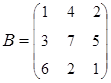 .
.
3. Найти А–1, где: 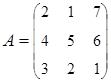 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ=  матричным способом.
матричным способом.
4. Решить систему а) методом Крамера; б) методом Гаусса:
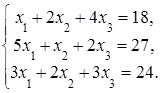 Сделать проверку.
Сделать проверку.
5. Даны стороны треугольника 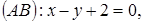
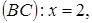
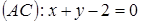 .Составить уравнение прямой, проходящей через вершину B и через точку на стороне AC, делящую ее (считая от А) в отношении 1:3.
.Составить уравнение прямой, проходящей через вершину B и через точку на стороне AC, делящую ее (считая от А) в отношении 1:3.
6. Линия задана уравнением r=r(φ) в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от φ=0 до φ=2π и придавая φ значения через промежуток π/8; 2) найти уравнение данной линии в прямоугольной декартовой системе координат, у которой начало совпадает с полюсом, а положительная ось абсцисс – с полярной осью; 3) по полученному уравнению определить, какая это линия.
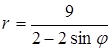 .
.
7. Даны координаты вершин пирамиды  .
.
Найти: 1) длину ребра  ; 2) угол между ребрами
; 2) угол между ребрами  и
и 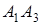 ; 3) угол между ребром
; 3) угол между ребром 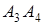 и гранью
и гранью 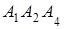 ; 4) площадь грани
; 4) площадь грани 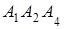 ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж.
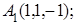
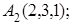
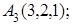
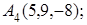
8. Найти точку К, симметричную точке М(2, 1, 0) относительно плоскости у+z+2=0.
1. Вычислить определитель: 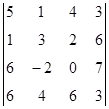 .
.
2. Найти АВ–ВА, где: 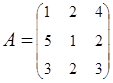 ;
; 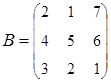 .
.
3. Найти А–1, где: 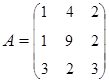 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ=  матричным способом.
матричным способом.
4. Решить систему а) методом Крамера; б) методом Гаусса:
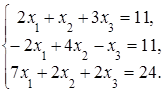 Сделать проверку.
Сделать проверку.
5. Уравнение одной из сторон квадрата 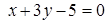 . Составить уравнения трех остальных сторон квадрата, если (–1,0) – точка пересечения его диагоналей.
. Составить уравнения трех остальных сторон квадрата, если (–1,0) – точка пересечения его диагоналей.
6. Линия задана уравнением r=r(φ) в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от φ=0 до φ=2π и придавая φ значения через промежуток π/8; 2) найти уравнение данной линии в прямоугольной декартовой системе координат, у которой начало совпадает с полюсом, а положительная ось абсцисс – с полярной осью; 3) по полученному уравнению определить, какая это линия.
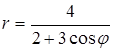 .
.
7. Даны координаты вершин пирамиды  .
.
Найти: 1) длину ребра 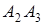 ; 2) угол между ребрами
; 2) угол между ребрами 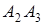 и
и 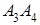 ; 3) угол между ребром
; 3) угол между ребром 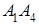 и гранью
и гранью  ; 4) площадь грани
; 4) площадь грани  ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж.
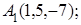
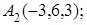
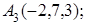
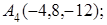
8. Найти проекцию точки М(1, 0, –1) на прямую 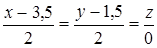
1. Вычислить определитель: 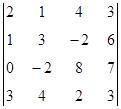 .
.
2. Найти АВ–ВА, где: 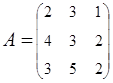 ;
; 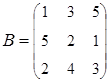 .
.
3. Найти А–1, где: 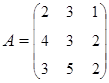 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ=  матричным способом.
матричным способом.
4. Решить систему а) методом Крамера; б) методом Гаусса:
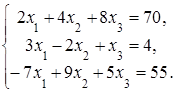 Сделать проверку.
Сделать проверку.
5. Даны уравнения двух сторон прямоугольника 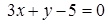 ,
, 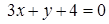 и уравнение его диагонали
и уравнение его диагонали 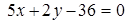 . Составить уравнения остальных сторон и второй диагонали этого прямоугольника.
. Составить уравнения остальных сторон и второй диагонали этого прямоугольника.
6. Линия задана уравнением r=r(φ) в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от φ=0 до φ=2π и придавая φ значения через промежуток π/8; 2) найти уравнение данной линии в прямоугольной декартовой системе координат, у которой начало совпадает с полюсом, а положительная ось абсцисс – с полярной осью; 3) по полученному уравнению определить, какая это линия.
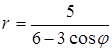 .
.
7. Даны координаты вершин пирамиды  .
.
Найти: 1) длину ребра  ; 2) угол между ребрами
; 2) угол между ребрами 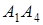 и
и 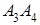 ; 3) угол между ребром
; 3) угол между ребром 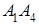 и гранью
и гранью  ; 4) площадь грани
; 4) площадь грани  ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж.
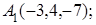
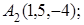
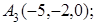
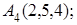
8. Найти проекцию точки Р(–1, 2, 0) на плоскость 4х–5у–z–7=0.
1. Вычислить определитель: 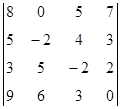 .
.
2. Найти АВ–ВА, где: 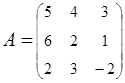 ;
; 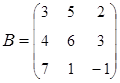 .
.
3. Найти А–1, где: 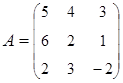 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ=  матричным способом.
матричным способом.
4. Решить систему а) методом Крамера; б) методом Гаусса:
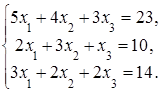 Сделать проверку.
Сделать проверку.
5. Даны вершины треугольника ABC: А(2,–2); B(3,–5); C(5,7). Составить уравнение медиан, проведенных из вершин A и C.
6. Линия задана уравнением r=r(φ) в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от φ=0 до φ=2π и придавая φ значения через промежуток π/8; 2) найти уравнение данной линии в прямоугольной декартовой системе координат, у которой начало совпадает с полюсом, а положительная ось абсцисс – с полярной осью; 3) по полученному уравнению определить, какая это линия.
 .
.
7. Даны координаты вершин пирамиды  .
.
Найти: 1) длину ребра 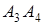 ; 2) угол между ребрами
; 2) угол между ребрами  и
и 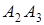 ; 3) угол между ребром
; 3) угол между ребром 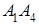 и гранью
и гранью 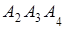 ; 4) площадь грани
; 4) площадь грани 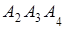 ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж. 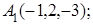
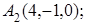
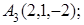
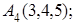
8. Найти точку К, симметричную точке М(2, 1, 0) относительно прямой 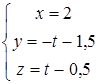
1. Вычислить определитель: 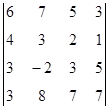 .
.
2. Найти АВ–ВА, где: 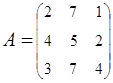 ;
; 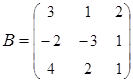 .
.
3. Найти А–1, где: 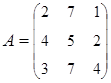 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ=  матричным способом.
матричным способом.
4. Решить систему а) методом Крамера; б) методом Гаусса:
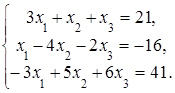 Сделать проверку.
Сделать проверку.
5. Стороны треугольника заданы уравнениями 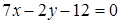 ,
, 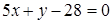 ,
, 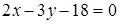 . Найти середины сторон треугольника.
. Найти середины сторон треугольника.
6. Линия задана уравнением r=r(φ) в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от φ=0 до φ=2π и придавая φ значения через промежуток π/8; 2) найти уравнение данной линии в прямоугольной декартовой системе координат, у которой начало совпадает с полюсом, а положительная ось абсцисс – с полярной осью; 3) по полученному уравнению определить, какая это линия.
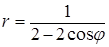 .
.
7. Даны координаты вершин пирамиды  .
.
Найти: 1) длину ребра 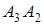 ; 2) угол между ребрами
; 2) угол между ребрами  и
и 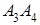 ; 3) угол между ребром
; 3) угол между ребром 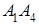 и гранью
и гранью  ; 4) площадь грани
; 4) площадь грани  ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж.
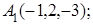
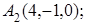
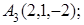
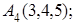
8. Найти точку L, симметричную точке К относительно прямой 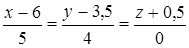 .
.
1. Вычислить определитель: 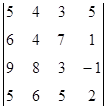 .
.
2. Найти АВ–ВА, где: 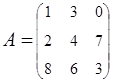 ;
; 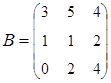 .
.
3. Найти А–1, где: 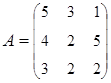 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ=  матричным способом.
матричным способом.
4. Решить систему а) методом Крамера; б) методом Гаусса:
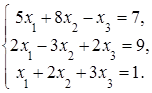 Сделать проверку.
Сделать проверку.
5. Стороны треугольника ВАС заданы уравнениями: 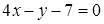 ,
, 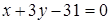 ,
, 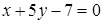 .Найти уравнение средней линии треугольника, проходящей через середины сторон АВ и ВС.
.Найти уравнение средней линии треугольника, проходящей через середины сторон АВ и ВС.
6. Линия задана уравнением r=r(φ) в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от φ=0 до φ=2π и придавая φ значения через промежуток π/8; 2) найти уравнение данной линии в прямоугольной декартовой системе координат, у которой начало совпадает с полюсом, а положительная ось абсцисс – с полярной осью; 3) по полученному уравнению определить, какая это линия.
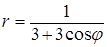 .
.
7. Даны координаты вершин пирамиды  .
.
Найти: 1) длину ребра 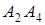 ; 2) угол между ребрами
; 2) угол между ребрами  и
и 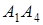 ; 3) угол между ребром
; 3) угол между ребром 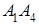 и гранью
и гранью  ; 4) площадь грани
; 4) площадь грани  ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж.
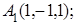
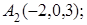
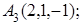
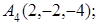
8. Найти точку В, симметричную точке С(1, 0, –1) относительно плоскости 2у+4z–1=0.
1. Вычислить определитель:  .
.
2. Найти АВ–ВА, где: 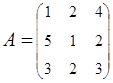 ;
; 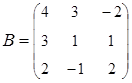 .
.
3. Найти А–1, где: 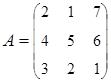 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ=  матричным способом.
матричным способом.
4. Решить систему а) методом Крамера; б) методом Гаусса:
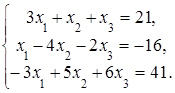 Сделать проверку.
Сделать проверку.
5. Даны вершины А(3,2); B(5,2); C(1,0). Составить уравнение биссектрисы его внутреннего угла при вершине B.
6. Линия задана уравнением r=r(φ) в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от φ=0 до φ=2π и придавая φ значения через промежуток π/8; 2) найти уравнение данной линии в прямоугольной декартовой системе координат, у которой начало совпадает с полюсом, а положительная ось абсцисс – с полярной осью; 3) по полученному уравнению определить, какая это линия.
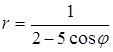 .
.
7. Даны координаты вершин пирамиды  .
.
Найти: 1) длину ребра 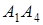 ; 2) угол между ребрами
; 2) угол между ребрами 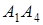 и
и 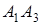 ; 3) угол между ребром
; 3) угол между ребром 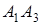 и гранью
и гранью 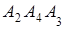 ; 4) площадь грани
; 4) площадь грани 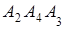 ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж.
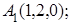
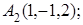
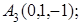
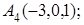
8. Найти проекцию точки Р(1, 1, 1) на плоскость х+4у+3z+5=0.
1. Вычислить определитель: 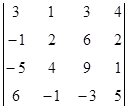 .
.
2. Найти АВ–ВА, где: 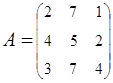 ;
; 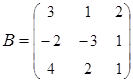 .
.
3. Найти А–1, где: 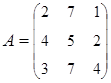 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ=  матричным способом.
матричным способом.
4. Решить систему а) методом Крамера; б) методом Гаусса:
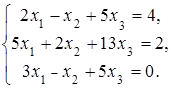 Сделать проверку.
Сделать проверку.
5. Даны уравнения двух смежных сторон параллелограмма 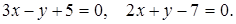 Найти угол, образованный этими сторонами и уравнения двух других сторон параллелограмма.
Найти угол, образованный этими сторонами и уравнения двух других сторон параллелограмма.
6. Линия задана уравнением r=r(φ) в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от φ=0 до φ=2π и придавая φ значения через промежуток π/8; 2) найти уравнение данной линии в прямоугольной декартовой системе координат, у которой начало совпадает с полюсом, а положительная ось абсцисс – с полярной осью; 3) по полученному уравнению определить, какая это линия.
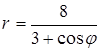 .
.
7. Даны координаты вершин пирамиды  . Найти: 1) длину ребра
. Найти: 1) длину ребра 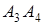 ; 2) угол между ребрами
; 2) угол между ребрами 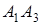 и
и 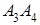 ; 3) угол между ребром
; 3) угол между ребром 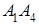 и гранью
и гранью 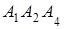 ; 4) площадь грани
; 4) площадь грани 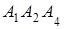 ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж. 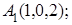
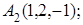
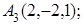
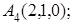
8. Найти точку К, симметричную точке М(–1, 0, –1) относительно прямой 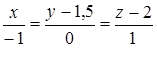 .
.
1. Вычислить определитель: 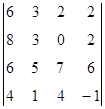 .
.
2. Найти АВ–ВА, где: 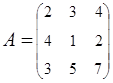 ;
; 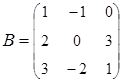 .
.
3. Найти А–1, где: 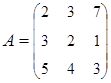 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ=  матричным способом.
матричным способом.
4. Решить систему а) методом Крамера; б) методом Гаусса:
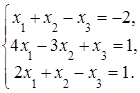 Сделать проверку.
Сделать проверку.
5. Даны уравнения трех сторон треугольника ABC 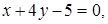
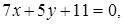
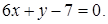 Найти точку P пересечения медиан треугольника.
Найти точку P пересечения медиан треугольника.
6. Линия задана уравнением r=r(φ) в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от φ=0 до φ=2π и придавая φ значения через промежуток π/8; 2) найти уравнение данной линии в прямоугольной декартовой системе координат, у которой начало совпадает с полюсом, а положительная ось абсцисс – с полярной осью; 3) по полученному уравнению определить, какая это линия.
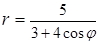 .
.
7. Даны координаты вершин пирамиды  .
.
Найти: 1) длину ребра 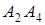 ; 2) угол между ребрами
; 2) угол между ребрами 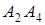 и
и 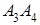 ; 3) угол между ребром
; 3) угол между ребром 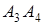 и гранью
и гранью 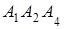 ; 4) площадь грани
; 4) площадь грани 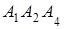 ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж.
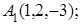
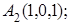
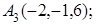
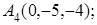
8. Найти точку N, симметричную точке M(1, 2, 3) относительно плоскости 2х+10у+10z–1=0.
1. Вычислить определитель: 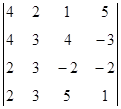 .
.
2. Найти АВ–ВА, где: 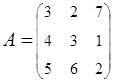 ;
; 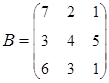 .
.
3. Найти А–1, где: 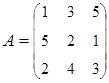 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ=  матричным способом.
матричным способом.
4.Решить систему а) методом Крамера; б) методом Гаусса:
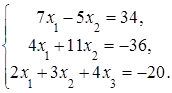 Сделать проверку.
Сделать проверку.
5. Дан треугольник с вершинами A(–8,3); B(8,5); C(8,–5). Найти точку пересечения его высот.
6. Линия задана уравнением r=r(φ) в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от φ=0 до φ=2π и придавая φ значения через промежуток π/8; 2) найти уравнение данной линии в прямоугольной декартовой системе координат, у которой начало совпадает с полюсом, а положительная ось абсцисс – с полярной осью; 3) по полученному уравнению определить, какая это линия.
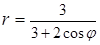 .
.
7. Даны координаты вершин пирамиды  .
.
Найти: 1) длину ребра 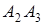 ; 2) угол между ребрами
; 2) угол между ребрами 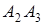 и
и 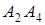 ; 3) угол между ребром
; 3) угол между ребром 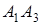 и гранью
и гранью 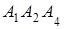 ; 4) площадь грани
; 4) площадь грани 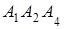 ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж.
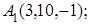
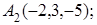
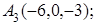
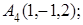
8. Найти проекцию точки М(0, 2, 1) на прямую 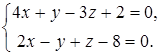
1. Вычислить определитель: 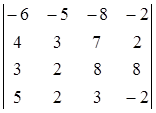 .
.
2. Найти АВ–ВА, где: 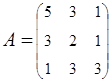 ;
; 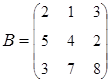 .
.
3. Найти А–1, где: 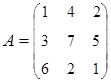 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ=  матричным способом.
матричным способом.
4. Решить систему а) методом Крамера; б) методом Гаусса:
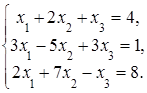 Сделать проверку.
Сделать проверку.
5. Даны уравнения двух сторон параллелограмма 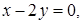
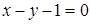 и точка пересечения диагоналей M(3,–1). Найти уравнения двух других сторон.
и точка пересечения диагоналей M(3,–1). Найти уравнения двух других сторон.
6. Линия задана уравнением r=r(φ) в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от φ=0 до φ=2π и придавая φ значения через промежуток π/8; 2) найти уравнение данной линии в прямоугольной декартовой системе координат, у которой начало совпадает с полюсом, а положительная ось абсцисс – с полярной осью; 3) по полученному уравнению определить, какая это линия.
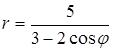 .
.
7. Даны координаты вершин пирамиды  .
.
Найти: 1) длину ребра  ; 2) угол между ребрами
; 2) угол между ребрами  и
и 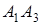 ; 3) угол между ребром
; 3) угол между ребром 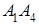 и гранью
и гранью  ; 4) площадь грани
; 4) площадь грани  ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж.
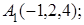
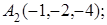
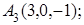
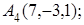
8. Найти проекцию точки N(1, 0, –1) на плоскость 2у+4z–1=0.
5. Вычислить определитель: 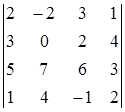 .
.
6. Найти АВ–ВА, где: 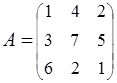 ;
; 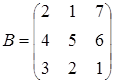 .
.
7. Найти А-1, где: 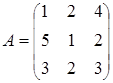 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ=  матричным способом.
матричным способом.
8. Решить систему а) методом Крамера; б) методом Гаусса:
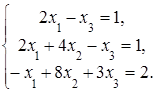 Сделать проверку.
Сделать проверку.
5. Три стороны треугольника АВС заданы уравнениями: (АВ): х-3у–23=0; (ВС): 7х+9у+19=0; (АС): 4х+3у+13=0. Составить уравнение высоты, проведенной из вершины В и уравнение медианы, проведенной из вершины А.
6. Линия задана уравнением r=r(φ) в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от φ=0 до φ=2π и придавая φ значения через промежуток π/8; 2) найти уравнение данной линии в прямоугольной декартовой системе координат, у которой начало совпадает с полюсом, а положительная ось абсцисс – с полярной осью; 3) по полученному уравнению определить, какая это линия.
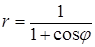 .
.
7. Даны координаты вершин пирамиды  .
.
Найти: 1) длину ребра  ; 2) угол между ребрами
; 2) угол между ребрами  и
и 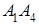 ; 3) угол между ребром
; 3) угол между ребром 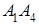 и гранью
и гранью  ; 4) площадь грани
; 4) площадь грани  ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж.
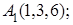
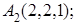
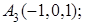
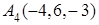 .
.
8. Найти точку В, симметричную точке А(1, 3, –4) относительно плоскости 3х+у–2z=0.
1. Вычислить определитель: 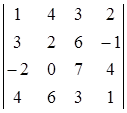 .
.
2. Найти АВ–ВА, где: 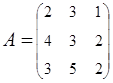 ;
; 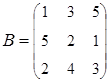 .
.
3. Найти А–1, где: 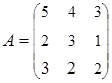 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ=  матричным способом.
матричным способом.
4. Решить систему а) методом Крамера; б) методом Гаусса:
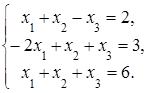 Сделать проверку.
Сделать проверку.
5. Даны уравнения одной из сторон ромба 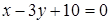 и одной из его диагоналей
и одной из его диагоналей 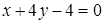 ; диагонали ромба пересекаются в точке
; диагонали ромба пересекаются в точке 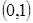 .
.
Найти уравнения остальных сторон ромба.
6. Линия задана уравнением r=r(φ) в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от φ=0 до φ=2π и придавая φ значения через промежуток π/8; 2) найти уравнение данной линии в прямоугольной декартовой системе координат, у которой начало совпадает с полюсом, а положительная ось абсцисс – с полярной осью; 3) по полученному уравнению определить, какая это линия.
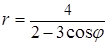 .
.
7. Даны координаты вершин пирамиды 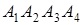 .
.
Найти: 1) длину ребра 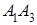 ; 2) угол между ребрами
; 2) угол между ребрами  и
и 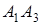 ; 3) угол между ребром
; 3) угол между ребром 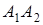 и гранью
и гранью 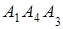 ; 4) площадь грани
; 4) площадь грани 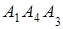 ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж.
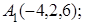
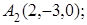
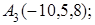
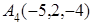 .
.
8. Найти точку М, симметричную точке N(1, 3, 5) относительно плоскости 2х–у–3z+5=0.
1. Вычислить определитель: 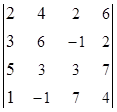 .
.
2. Найти АВ–ВА, где: 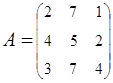 ;
; 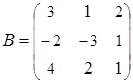 .
.
3. Найти А–1, где: 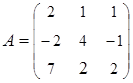 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ=  матричным способом.
матричным способом.
4. Решить систему а) методом Крамера; б) методом Гаусса:
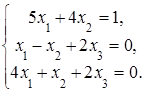 Сделать проверку.
Сделать проверку.
5. Даны две вершины 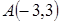 и
и 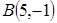 и точка
и точка 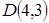 пересечения высот треугольника. Составить уравнения его сторон.
пересечения высот треугольника. Составить уравнения его сторон.
6. Линия задана уравнением r=r(φ) в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от φ=0 до φ=2π и придавая φ значения через промежуток π/8; 2) найти уравнение данной линии в прямоугольной декартовой системе координат, у которой начало совпадает с полюсом, а положительная ось абсцисс – с полярной осью; 3) по полученному уравнению определить, какая это линия.
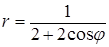 .
.
7. Даны координаты вершин пирамиды  .
.
Найти: 1) длину ребра 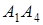 ; 2) угол между ребрами
; 2) угол между ребрами  и
и 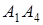 ; 3) угол между ребром
; 3) угол между ребром 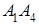 и гранью
и гранью  ; 4) площадь грани
; 4) площадь грани  ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж.
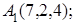
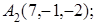
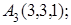
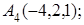
8. Найти проекцию точки Р(2, –5,7) на прямую, проходящую через точки М1(4, 5, 6) и М2(–2, –17, –8).
1. Вычислить определитель: 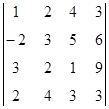 .
.
2. Найти АВ–ВА, где: 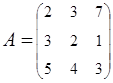 ;
; 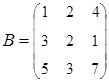 .
.
3. Найти А–1, где: 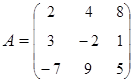 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ=  матричным способом.
матричным способом.
4. Решить систему а) методом Крамера; б) методом Гаусса:
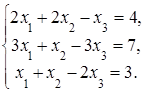 Сделать проверку.
Сделать проверку.
5. Уравнения двух сторон параллелограмма 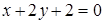 и
и 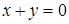 , а уравнение одной из его диагоналей
, а уравнение одной из его диагоналей 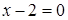 .Найти координаты вершин параллелограмма.
.Найти координаты вершин параллелограмма.
6. Линия задана уравнением r=r(φ) в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от φ=0 до φ=2π и придавая φ значения через промежуток π/8; 2) найти уравнение данной линии в прямоугольной декартовой системе координат, у которой начало совпадает с полюсом, а положительная ось абсцисс – с полярной осью; 3) по полученному уравнению определить, какая это линия.
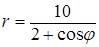 .
.
7. Даны координаты вершин пирамиды  .
.
Найти: 1) длину ребра 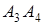 ; 2) угол между ребрами
; 2) угол между ребрами  и
и 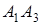 ; 3) угол между ребром
; 3) угол между ребром 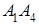 и гранью
и гранью  ; 4) площадь грани
; 4) площадь грани 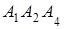 ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж.
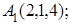
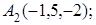
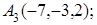
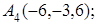
8. Найти точку Q, симметричную точке Р(4, 1, 6) относительно прямой
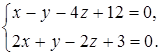
1. Вычислить определитель: 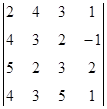 .
.
2. Найти АВ–ВА, где: 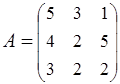 ;
; 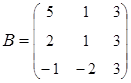 .
.
3. Найти А–1, где: 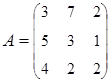 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ=  матричным способом.
матричным способом.
4. Решить систему а) методом Крамера; б) методом Гаусса:
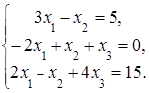 Сделать проверку.
Сделать проверку.
5. Три стороны треугольника 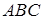 заданы уравнениями
заданы уравнениями 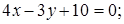
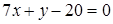 и
и 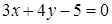 . Написать уравнение высоты и биссектрисы, проведенных из вершины
. Написать уравнение высоты и биссектрисы, проведенных из вершины  .
.
6. Линия задана уравнением r=r(φ) в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от φ=0 до φ=2π и придавая φ значения через промежуток π/8; 2) найти уравнение данной линии в прямоугольной декартовой системе координат, у которой начало совпадает с полюсом, а положительная ось абсцисс – с полярной осью; 3) по полученному уравнению определить, какая это линия.
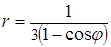 .
.
7. Даны координаты вершин пирамиды  .
.
Найти: 1) длину ребра 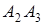 ; 2) угол между ребрами
; 2) угол между ребрами 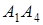 и
и 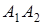 ; 3) угол между ребром
; 3) угол между ребром 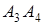 и гранью
и гранью  ; 4) площадь грани
; 4) площадь грани  ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж.
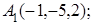
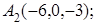
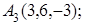
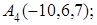
8. Найти точку Q, симметричную точке Р(2, –5, 7) относительно прямой
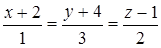
1. Вычислить определитель: 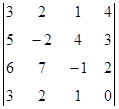 .
.
2. Найти АВ–ВА, где: 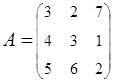 ;
; 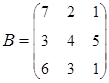 .
.
3. Найти А–1, где: 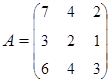 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ=  матричным способом.
матричным способом.
4. Решить систему а) методом Крамера; б) методом Гаусса:
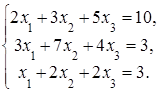 Сделать проверку.
Сделать проверку.
5. Даны вершины 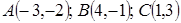 трапеции
трапеции 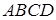
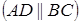 . Известно, что диагонали трапеции взаимно перпендикулярны. Найти координаты вершины
. Известно, что диагонали трапеции взаимно перпендикулярны. Найти координаты вершины 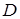 этой трапеции.
этой трапеции.
6. Линия задана уравнением r=r(φ) в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от φ=0 до φ=2π и придавая φ значения через промежуток π/8; 2) найти уравнение данной линии в прямоугольной декартовой системе координат, у которой начало совпадает с полюсом, а положительная ось абсцисс – с полярной осью; 3) по полученному уравнению определить, какая это линия.
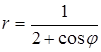 .
.
7. Даны координаты вершин пирамиды  .
.
Найти: 1) длину ребра 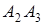 ; 2) угол между ребрами
; 2) угол между ребрами 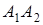 и
и 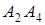 ; 3) угол между ребром
; 3) угол между ребром 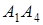 и гранью
и гранью 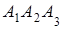 ; 4) площадь грани
; 4) площадь грани  ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж.
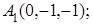
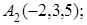
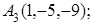
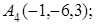
8. Найти проекцию точки А(2, 0, 3) на прямую 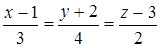 .
.
1. Вычислить определитель: 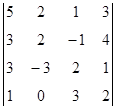 .
.
2. Найти АВ–ВА, где: 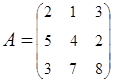 ;
; 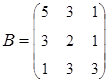 .
.
3. Найти А–1, где: 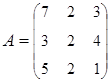 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ=  матричным способом.
матричным способом.
4. Решить систему а) методом Крамера; б) методом Гаусса:
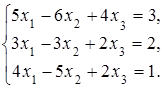 Сделать проверку.
Сделать проверку.
5. Даны уравнения двух сторон треугольника 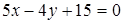 и
и 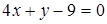 . Его медианы пересекаются в точке
. Его медианы пересекаются в точке 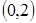 .Составить уравнение третьей стороны треугольника.
.Составить уравнение третьей стороны треугольника.
6. Линия задана уравнением r=r(φ) в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от φ=0 до φ=2π и придавая φ значения через промежуток π/8; 2) найти уравнение данной линии в прямоугольной декартовой системе координат, у которой начало совпадает с полюсом, а положительная ось абсцисс – с полярной осью; 3) по полученному уравнению определить, какая это линия.
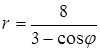 .
.
7. Даны координаты вершин пирамиды  .
.
Найти: 1) длину ребра 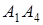 ; 2) угол между ребрами
; 2) угол между ребрами 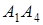 и
и 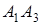 ; 3) угол между ребром
; 3) угол между ребром 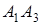 и гранью
и гранью 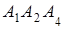 ; 4) площадь грани
; 4) площадь грани 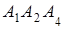 ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж.
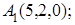
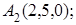
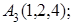
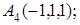
8. Найти проекцию точки А(1, –1, 2) на плоскость х+у+2z–3=0.
1. Вычислить определитель: 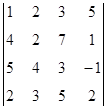 .
.
2. Найти АВ–ВА, где: 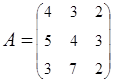 ;
; 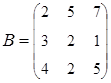 .
.
3. Найти А–1, где: 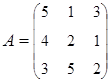 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ=  матричным способом.
матричным способом.
4. Решить систему а) методом Крамера; б) методом Гаусса:
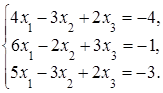 Сделать проверку.
Сделать проверку.
5. Даны две вершины 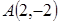 и
и 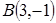 и точка
и точка 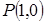 пересечения медиан треугольника
пересечения медиан треугольника 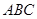 . Составить уравнение высоты треугольника, проведенной через третью вершину С.
. Составить уравнение высоты треугольника, проведенной через третью вершину С.
6. Линия задана уравнением r=r(φ) в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от φ=0 до φ=2π и придавая φ значения через промежуток π/8; 2) найти уравнение данной линии в прямоугольной декартовой системе координат, у которой начало совпадает с полюсом, а положительная ось абсцисс – с полярной осью; 3) по полученному уравнению определить, какая это линия.
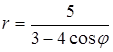 .
.
7. Даны координаты вершин пирамиды  .
.
Найти: 1) длину ребра  ; 2) угол между ребрами
; 2) угол между ребрами  и
и 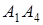 ; 3) угол между ребром
; 3) угол между ребром 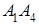 и гранью
и гранью  ; 4) площадь грани
; 4) площадь грани  ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж.

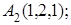
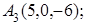
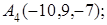
8. Найти проекцию точки М(0, –3, –2) на прямую 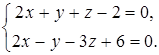
Listen to spoken English from multiple sources as much as possible. Listen to English spoken movies and English spoken TV channels, listen to the radio and as many other listening sources as you may find. It would be better if your passages are academic or close to what is in TOEFL iBT. The more you practice listening, the better listener you will become.
Listen for the main idea. It is usually found at the beginning of the listening passages, while the details are dispersed throughout the lecture. The main idea will give you understanding of what the conversation/lecture is about. Then you may listen for details.
Learn to find how the ideas are presented in the listening passage. Some of the main relations between ideas include cause/effect, compare/contrast, and steps in a process.
Learn to listen for signal words that indicate different part of the passage - introduction, major steps, examples, conclusions, etc.
Build your vocabulary. While listening, try to guess the meaning of unfamiliar words from context. It is very important since there is a big chance to come across words you don't know at the real test. Then, you should guess their meaning. Write down every word you don't know and include it in your wordlist. Try to memorize it and use it in your speaking and writing. Flashcards could be a great way to improve your vocabulary.
Listen to conversations or lectures with variety of accents. In TOEFL iBT Listening section there is a variety of accents and pronunciations. For this reason, you should practice listening to a people with different accents and pronunciation patterns.
Practice note-taking. Note-taking is allowed during all sections of TOEFL iBT. Effective note-taking may highly improve your performance. It is almost impossible to memorize all clues and details provided in the Listening section. Moreover, you can hear the passages ONLY ONCE. Therefore, to answer the questions you have to rely on what you remember from the passage and your notes. See also our Effective Note-Taking Strategies.
Summarize in writing what you have heard, using your notes. Thus, you will learn to find the purpose and main idea of the listening, and also the most important details. You will also learn to take and use notes. It also helps in improving your writing skills.
Familiarize yourself with the type of questions in TOEFL iBT. Make sure that during the preparation you learn what answers are required by the different types of question. Some questions may ask you to provide two answers, others to click in a chart box. If you are familiar with the question types, you may save important time.
At the exam strategies
Forget about the Reading section. Now it is time to fully concentrate on the Listening section.
The clock is ticking only when you are answering the questions and not when you are listening to the passages. So, when you listen, forget about the clock.
Prepare for note-taking. Before the section starts, write down the words 'main idea', 'major points', and 'important details'. Under which word you will place your notes from the listening passage.
Do not be distracted by the speaker's accent, speaking style and delivery. Focus on the content and flow of information the speaker(s) deliver.
Listen to find clues that will help you understand what the speaker's purpose, attitude and degree of certainty is. Listen for words that show relationship between ideas.
Pay attention to the visual materials. Some of the visual materials in the Listening section bring important information. Blackboards show important words or phrases that are discussed during the lecture. Illustrations and graphics support the information presented in the lecture. They are available only when the lecturer refers to them.
Answering is different. In the Listening section you may not return to the previous questions to correct your answers. Nevertheless, you have to confirm twice that you want to move to the next question. First, when you provide your answer you have to press the NEXT button. After pressing the NEXT button you may alter you answer. To move to the next question you have to press OK button. Sometimes test takers forget this and lose important time. Please, set your mind that you have to press two buttons.
Take a guess. There is no penalty for an incorrect answer in TOEFL iBT. It doesn't bring any points. If you see you are running out of time, just take a guess and mark answers for all remaining questions. There is 25 % chance to guess the right answer.
| <== previous lecture | | | next lecture ==> |
| Маркетинг как парадокс | | | ОРГАНИЗАЦИОННО-МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ |