Векторная алгебра. Аналитическая геометрия.

Date: 2015-10-07; view: 401.

TextB

Demand

The first thing to understand is that demand is not the same thing as desire, or need, or want. We are looking for the forces which determine price, and the strength of the desire for something will not, in itself, have any influ­ence on the price. Only when desire is supported by the ability and willingness to pay the price does it become an effective demand and has an influence in the market. Demand, in economics, means effective demand, and may be defined as 'the quantity of the commodity which will be demanded at any given price over some given period of time'.

Consider the following statements:

10. The demand for commodity X is 1 000 units.

11. The demand for commodity X, at a price of 6 p per unit, is I 000 units.

12. The demand for commodity X, at a price of 6 p per unit, is 1 000 units per week.

Note that only the third statement is meaningful. The first statement is incomplete because the quantity demand­ed will be different at different price. The second statement tells us the quantity demanded at given price, but it does not tell us how long it will take to sell 1 000 units. Any definition of demand must say something about the quantity, the price, and the time period.

For the great majority of goods and services, experience show that the quantity demanded will increase as the price falls. This particular characteristic of demand may be illus­trated by a table described asademand schedule, or, as is more usual, byademand curve, which is a graphical representation of the date in the demand schedule.

1. Заданы векторы , , . Найти:

а) длину и направляющие косинусы вектора ;

б) проекцию вектора на направление вектора ;

в) угол между векторами и ;

г) длину высоты параллелепипеда, построенного на векторах , , , если векторы и образуют его основание.

2. Вершины треугольника помещены в точках A, B, C. Найти:

а) точку пересечения медиан;

б) величину внутреннего угла С;

в) длину и уравнение высоты СD;

г) уравнение прямой, которая проход через точку А параллельно прямой ВС.

№ варианта	№1, 2
	A	B	C
	(1;-2;0)	(-4;3;0)	(5;7;0)
	(-1;2;0)	(5;-3;0)	(2;5;0)	{-7;1;-3}	{8;-9;2}
	(6;4;0)	(-2;-1;0)	(8;-9;0)	{4;-2;2}	{-3;5;4}
	(3;0;0)	(7;-4;0)	(5;-3;0)	{2;3;-1}	{6;-4;5}
	(2;-3;0)	(1;5;0)	(-6;-8;0)	{0;2;3}	{7;3;-4}
	(1;2;0)	(7;4;0)	(3;-4;0)
	(1;3;0)	(1;0;0)	(2;-2;0)	{2;1;3}	{3;-1;2}
	(1;2;0)	(-1;-1;0)	(2;1;0)	{2;4;4}	{1;2;3}
	(2;-2;0)	(3;-6;0)	(-1;3;0)	{-2;4;-4}	{2;2;1}
	(2;-3;0)	(8;-3;0)	(-2;4;0)	{1;1;3}	{0;2;-1}
	(-1;4;0)	(5;-4;0)	(8;-3;0)
	(2;-5;0)	(6;3;0)	(-6;4;0)	{1;3;2}	{1;-1;4}
	(-1;-4;0)	(3;7;0)	(4;4;0)	{3;2-5;}	{1;-3;1}
	(-4;3;0)	(2;4;0)	(-4;8;0)	{3;2;-5}	{2;1;-1}
	(4;2;0)	(7;-2;0)	(1;6;0)	{1;3;-1}	{0;-1;3}
	(5;-1;0)	(-6;1;0)	(2;4;0)	{2;-1;0}	{6;-7;2}
	(1;3;0)	(2;4;0)	(-3;2;0)	{-1;2;-3}	{2;-3;-4}
	(-5;3;0)	(1;4;0)	(-1;-1;0)	{1;1;1}	{1;1;-4}
	(-5;3;0)	(5;7;0)	(4;-3;0)	{1;1;-2}	{0;1;-3}
	(6;9;0)	(-3;4;0)	(4;-5;0)	{0;1;-3}	{1;-1;-2}
	(1;2;0)	(3;0;0)	(5;2;0)
	(-2;3;0)	(6;-2;0)	(4;1;0)	{-3;-4;2}	{5;3;-6}
	(1;2;0)	(-1;3;0)	(2;5;0)	{2;-3;-4}	{-3;12;6}
	(1;3;0)	(4;3;0)	(-1;2;0)	{-3;2;3}	{1;0;-2}
	(-2;3;0)	(2;4;0)	(1;-5;0)	{-5;-3;1}	{0;-3;4}
	(-4;0;6)	(1;0;5)	(-1;0;-2)	{-1;-1;1}	{-2;4;2}
	(-3;0;2)	(-2;0;-6)	(5;0;3)	{1;-1;3}	{4;8; }
	(6;-3;0)	(-2;5;0)	(1;1;0)	{3;-3; }	{-2;4; }
	(7;2;0)	(3;4;0)	(-1;-2;0)	{2;-4; }	{- ;3;3}
	(-8;1;0)	(0;5;0)	(3;7;0)	{-1;1; 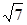}	{2;4; }