Определители матриц второго и третьего порядка.

Date: 2015-10-07; view: 459.

Каждой квадратной матрице ставится в соответствие число, обозначаемое

Рассмотрим определители для матриц второго и третьего порядков:

Пусть 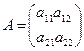,тогда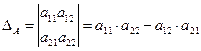

Из формулы следует, что определитель для матрицы второго порядка равен разности произведений элементов матрицы, стоящих на главной и побочной диагоналях.

Пусть 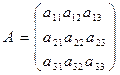, тогда

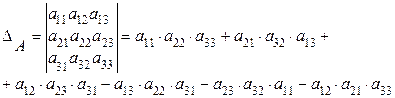
Существуют различные правила, позволяющие легко подсчитать те шесть слагаемых, из которых состоит определитель для матрицы третьего порядка.

Например, можно использовать «правило треугольников», которое условно показано на схемах 1 и 2 .

схема 1 схема 2

5. Обратная матрица и её нахождение.

Алгебраическим дополнением элемента а_ij квадратной матрицы 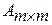называется число А_ij ,вычисляемое по формуле:

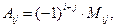где M_ij -определитель полученный из определителя матрицы 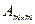удалением строки с номером i и столбца с номером j .

Матрица А^-1 называется обратной к матрице А, если

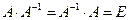,где Е - единичная матрица. Из определения следует, что матрицы А и А^-1 - квадратные матрицы одного порядка. Квадратная матрица имеет обратную, если ее определитель отличен от нуля и 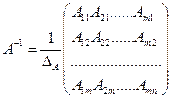, где А_ij -алгебраические дополнения элемента а_ij матрицы .