Теоретическая часть

Date: 2015-10-07; view: 401.

Цель работы

Терме

2. жыр

3. қоштасу

4. өлен

5. көңіл айту

606. Ауыз әдебиетінің асыл қазынасын жасап және ол өннерді атадан балаға таратқан талантты адамдар:

1. Ақындар

2. Жыраулар

3. Әншілер

4. импровизаторлар

5. Аталғандардың барлығы

Определение коэффициента Пуассона воздуха по данным измерения скорости распространения в нем звука методом стоячих волн.

Теплоемкостью тела называют количество теплоты, необходимое для повышения температуры тела на 1 К. Если телу сообщили количество теплоты d¢Q и при этом его температура изменилась на dT, то теплоемкость тела определяется как

. (2.1)

Для характеристики тепловых свойств веществ используют понятия удельной (с) и молярной (С) теплоемкости, определяемых как

и , (2.2)

где m - масса тела;

n - число молей вещества.

Теплоемкости C_m, c и C зависят от природы вещества и от условий в которых происходит нагревание. Это следует из первого начала термодинамики

(2.3)

Поскольку

, (2.4)

где dV – изменение объема тела;

P – давление.

то из (2.2) и (2.3) следует, что молярная теплоемкость физически однородного вещества определяется соотношением

(2.5)

Внутренняяэнергияидеальногогаза – энергия теплового движения молекул и атомов в молекулах и представляет собой сумму кинетической энергии поступательного и вращательного движения молекул и энергии колебания атомов. Средняя энергия молекулы идеального газа равна

, (2.6)

где i – сумма числа поступательных, вращательных и удвоенного числа колебательных степеней свободы молекулы.

Внутренняя энергия g молей газа равна

, (2.7)

где N_A – число Авогадро;

R – универсальная газовая постоянная.

В соответствии с (2.5) и (2.7) молярная теплоемкость идеального газа при постоянном объеме равна

. (2.8)

Из уравнения состояния идеального газа имеем

. (2.9)

При постоянном давлении

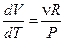. (2.10)

Из (2.5) с учетом (2.8) и (2.10) следует, что молярная теплоемкость идеального газа при постоянном давлении равна

. (2.11)

Отношение теплоемкостей газа при постоянном давлении и объеме

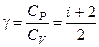(2.12)

называется коэффициентомПуассона. Это отношение определяется только числом степеней свободы молекулы газа.

Продольные волны в сплошной среде распространяются со скоростью

, (2.13)

где 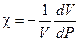- коэффициент сжимаемости среды;

r - плотность среды.

При распространении звуковых волн в газе любая небольшая его часть периодически сжимается и разжимается. В местах сжатия газ нагревается, а в местах разрежения – охлаждается. В следствии малой теплопроводности газа и большой частоты колебаний можно считать газ теплоизолированным. В таком случае распространение звука в газе сопровождается адиабатическим сжатием и разрежением газа.

(2.14)

Дифференцируя по P

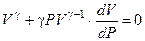, (2.15)

находим производную объема по давлению:

, (2.16)

откуда

и . (2.17)

Из уравнения Клапейрона-Менделеева следует, что

(2.18)

где m - молярная масса газа.

С учетом (2.17) и (2.18) получаем

(2.19)

В настоящей работе измерение скорости звука в воздухе основано на свойствах стоячих волн. Как показывают расчеты, резонанс в трубе будет в том случае, когда расстояние между торцами трубы будет равно целому числу длин полуволн:

, (2.20)

где n = 1, 2, 3 … - номер резонанса;

l_n – длина воздушного столба при резонансе соответствующего номера;

l - длина звуковой волны.

Выражая длину волны через частоту колебаний f и скорость распространения v, получаем:

. (2.21)

В соответствии с (2.21), графиком зависимости l_n(n) будет прямая линия, тангенс угла наклона j которой равен

, (2.22)

где n₁ и n₂ – номера резонансов;

l_n1 и l_n2 – соответствующие этим номерам расстояния между торцами трубы.

Следовательно, при известной частоте колебаний можно рассчитать скорость звука:

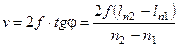. (2.23)