
Операции (высказывания) алгебры логики
Date: 2015-10-07; view: 871.
Основные понятия
Элементы алгебры логики
Алгебра логики или булева алгебра (ее разработчик – Дж. Буль) вытекает из логики, основу которой составили труды Аристотеля (384-322 гг до н. э.). Логика – наука о доказательных рассуждениях Правильность рассуждения определяется только его логической конструкцией (структурой), и не зависит конкретного содержания входящих в него рассуждений.
Математическая логика была создана во второй половине 19-го века, исчисления позволяют устранять неясности естественного языка. Математическая логика = Формальная логика + алгебраические операции.
Алгебра логики (булева алгебра) используется для описания логики функционирования аппаратных и программных средств вычислительной техники и представляет собой раздел математической логики, изучающий строение логических высказываний и способы установления их истинности с помощью алгебраических методов.
В алгебре логике все переменные и функции могут принимать только два значения 0 (Ложь, False) и 1 (истина, True).
Отношение между двумя высказываниями (или логическими функциями), когда для всех наборов значений аргументов значения функций на одинаковых наборах совпадают, называются эквивалентными. Логические выражения, истинные при любых значениях истинности входящих в них переменных, называют тавтологиями (от греч. “tauto” – то же самое и “logos” – слово).
Алгебра логики оперирует с высказываниями - грамматически правильными повествовательными предложениями, передающими смысл. Высказывание является истинным или ложным, простым или сложным, образованным из простых с помощью логических связок “и”, “или”, “не”, “если... , то” и т. п. Основные термины алгебры логики:
· простое высказывание – повествовательное предложение, принимающее одно из двух возможных значений – истина или ложь;
· предикат – высказывание с переменными, которое при одних значениях переменных может стать истинным высказыванием, при других – ложным;
· рассуждение – цепочка взаимосвязанных фактов и умозаключений, вытекающих друг из друга;
· составное высказывание – комбинация простых высказываний, соединенных логическими операциями.
Типы высказываний (основные операции алгебры логики):
1. Конъюнкция – логическое умножение (результат соединения высказываний с помощью связки “и”) дает сложное высказывание, истинное только тогда, когда истинны оба составляющие его высказывания обозначаются: x 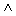 y или x & y или х×у, читается “х и у”.
y или x & y или х×у, читается “х и у”.
Обозначается Таблица истинности
на схемах & логического умножения
| X | Y | Х Ù Y |

2. Дизъюнкция – логическое сложение (результат соединения высказываний с помощью связки ”или”) дает сложное высказывание, истинное, когда истинно хотя бы одно из составляющих его высказываний. Обозначается x  y или x + y – дизъюнкция, читается “х или у”
y или x + y – дизъюнкция, читается “х или у”
Обозначается Таблица истинности
на схемах 1 логического сложения
| X | Y | Х Ú Y |

3. Строгая дизъюнкция (результат соединения высказываний с помощью связки “исключающее или”) дает сложное высказывание, истинное, когда истинно только одно из составляющих его высказываний (x  y или x
y или x  y - строгая дизъюнкция).
y - строгая дизъюнкция).
Таблица истинности
| X | Y | Х  Y Y
|
Иначе эта операция называется “сложение по модулю 2”, т.к. при сложении четного количества единиц результат будет 0, а при сложении нечетного количества единиц – 1.
4. Инверсия - логическое отрицание (результат применения к высказыванию связки “не”) дает сложное высказывание, истинное, когда исходное высказывание ложно ( 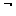 x или
x или  - инверсия).
- инверсия).
Обозначается инверсия Таблица истинности инверсии
| Х | 
|
на схемах

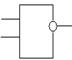
5. Импликация (следование) (результат соединения высказываний с помощью связки “если ... , то”) дает сложное высказывание, ложное, только когда первое из составляющих его высказываний истинно, а второе - ложно (x  y - импликация).
y - импликация).
Таблица истинности
импликации
| Х | Y | X  Y Y
|
6. Эквиваленция (результат соединения высказываний с помощью связки “тогда и только тогда”) дает сложное высказывание, истинное, когда истинность составляющих его высказываний совпадает (X « Y или X º Y - эквиваленция).
Эта операция называется также “эквивалентность” или равнозначность. Ее таблица истинности
| Х | Y | X«Y |
Алгебра логики вводит аксиомы и основные законы, с помощью которых можно упростить схемную реализацию компьютерных устройств или алгоритмов обработки информации, тем самым повысить надежность и сократить затраты на обработку информации. Используются также логические операторы - кванторы общности  (“для всех”) и существования
(“для всех”) и существования  (“существует”). Для сложных высказываний строятся таблицы истинности, например:
(“существует”). Для сложных высказываний строятся таблицы истинности, например:
| A | B | A 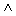 B B
| A  B B
| A  B B
|
| 0 (ЛОЖЬ) | 0 (ЛОЖЬ) | 0 (ЛОЖЬ) | 0 (ЛОЖЬ) | 1 (ИСТИНА) |
| 0 (ЛОЖЬ) | 1 (ИСТИНА) | 0 (ЛОЖЬ) | 1 (ИСТИНА) | 1 (ИСТИНА) |
| 1 (ИСТИНА) | 0 (ЛОЖЬ) | 0 (ЛОЖЬ) | 1 (ИСТИНА) | 0 (ЛОЖЬ) |
| 1 (ИСТИНА) | 1 (ИСТИНА) | 1 (ИСТИНА) | 1 (ИСТИНА) | 1 (ИСТИНА) |
| <== previous lecture | | | next lecture ==> |
| A Christmas Story | | | A. Закон тавтологии (многократное повторение) |