
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Движение тела по окружности с постоянной по модулю скоростью
Движение тела по окружности с постоянной по модулю скоростью — это движение, при котором тело за любые равные промежутки времени описывает одинаковые дуги.
Положение тела на окружности определяется радиусом-вектором r, проведенным из центра окружности. Модуль радиус-вектора равен радиусу окружности R (рис. 1).
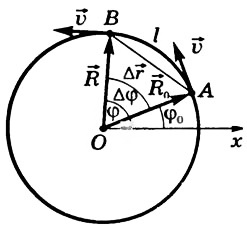
Рис. 1
За время Δt тело, двигаясь из точки А в точку В, совершает перемещение Δr, равное хорде АВ, и проходит путь, равный длине дуги l.
Радиус-вектор поворачивается на угол Δφ. Угол выражают в радианах.
Скорость υ движения тела по траектории (окружности) направлена по касательной к траектории. Она называется линейной скоростью.
Модуль линейной скорости равен отношению длины дуги окружности l к промежутку времени Δt за который эта дуга пройдена:
υ=lΔt.
Скалярная физическая величина, численно равная отношению угла поворота радиус-вектора к промежутку времени, за который этот поворот произошел, называется угловой скоростью:
ω=Δφ / Δt.
В СИ единицей угловой скорости является радиан в секунду (рад/с).
При равномерном движении по окружности угловая скорость и модуль линейной скорости — величины постоянные: ω = const; υ = const.
Положение тела можно определить, если известен модуль радиус-вектора r и угол φ, который он составляет с осью Ox (угловая координата). Если в начальный момент времени t0 = 0 угловая координата равна φ0, а в момент времени t она равна φ, то угол поворота Δφ радиус-вектора за время Δt=t−t0=t равен Δφ=φ−φ0. Тогда из последней формулы можно получить кинематическое уравнение движения материальной точки по окружности:
φ=φ0+ωt.
Оно позволяет определить положение тела в любой момент времени t. Учитывая, что Δφ=lR, получаем
ω=lR/Δt=υR
υ=ωR — формула связи между линейной и угловой скоростью.
Промежуток времени Τ, в течение которого тело совершает один полный оборот, называется периодом вращения:
T=Δt / N
где N — число оборотов, совершенных телом за время Δt.
За время Δt = Τ тело проходит путь l=2πR. Следовательно,
υ=2πRT
ω=2πT.
Величина ν, обратная периоду, показывающая, сколько оборотов совершает тело за единицу времени, называется частотой вращения:
ν=1/ T
T=N / Δt.
Следовательно,
υ=2πνR
ω=2πν.
| <== предыдущая страница | | | следующая страница ==> |
| Виды движения (равномерное, равноускоренное) и их графическое описание | | | Ускорение при движении по окружности с постоянной по модулю скоростью |
Дата добавления: 2014-02-26; просмотров: 1001; Нарушение авторских прав

Мы поможем в написании ваших работ!