
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Сетевые методы. Методы теории графов
Теория графов — это раздел математики, позволяющий исследовать объекты и процессы, имеющие многовариантные сетевые структуры, а также находить оптимальные сочетания вариантов, вместе составляющие единые цепи, пути, единые схемы и т. д.
В некотором смысле методы графов являются развитием методов вариантов, позволяющие решать экстремальные задачи на составленном графе. Данные методы являются комбинированными, как в части свойственных им графического и аналитического аспектов так и в части использования в них детерминированных методов и действий (конструирование графа) и методов вероятностно-статистических (оценка работ и свершения событий).
Во многих случаях отношения между элементами системы или объекта и их взаиморасположение можно изобразить в виде точек, связанных между собой линиями, т. е. представить в виде сетей. Отдельные точки (узлы) такой сети означают элементы системы, а линии (дуги), их связывающие,— отношения между ними. Такие схемы называются графами.
Предположим, что задан граф 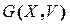 с множеством узлов (вершин)
с множеством узлов (вершин) 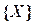 и множеством дуг
и множеством дуг 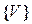 . Длина каждой дуги графа есть неотрицательное число
. Длина каждой дуги графа есть неотрицательное число 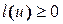 . Выберем на графе некоторый путь, условно обозначенный
. Выберем на графе некоторый путь, условно обозначенный 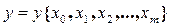 для которого справедливо
для которого справедливо 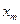 ≥
≥ 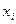 ≥
≥ 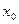 , при 0< i< m и
, при 0< i< m и 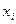

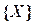 . Тогда длину этого выбранного пути может быть определена из выражения 2.14.
. Тогда длину этого выбранного пути может быть определена из выражения 2.14.
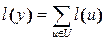 , 2.14
, 2.14
где U подмножество дуг составляющих путь 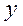 , проходящий через точки
, проходящий через точки 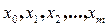 .
.
Задача заключается в том, чтобы на графе определить путь из 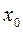 в
в 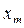 . с наименьшей (а может, и с наибольшей) длиной, т. е. необходимо определить
. с наименьшей (а может, и с наибольшей) длиной, т. е. необходимо определить
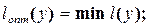 где
где 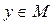 . 2.15
. 2.15
М — множество возможных путей из начальной точки (вершины) графа 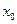 в конечную вершину
в конечную вершину 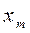 .
.
Таким образом, математически постановку задачи на графе можно свести к следующей модели, представляющей целевую функцию и систему ограничений:
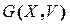 ;
;
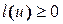 ;
;
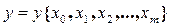 ;
;
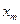 ≥
≥ 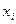 ≥
≥ 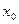 , при 0< i< m и
, при 0< i< m и 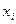

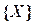 ;
;
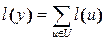 ;
;
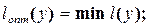
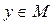 ;
;
Структура данной модели допускает последовательную детализацию узлов и дуг графа до необходимой степени от общего к частному. Методы теории графов находят успешное применение в решении многих технических, экономических и технологических задач. Так, например, теория графов привлекается для решения задач о нахождении кратчайшего пути между поставщиком и потребителем, задач о выборе рациональных средств транспорта по сети выработок шахты при заданных грузопотоках и длинах транспортирования, об определении рациональных параметров технологической схемы горного предприятия и т. д.
§3.6 Методы оптимизации на основе теории игр и статистических решений.
Одним из методов оптимизации являются методы теории игр. При решении практических задач гораздо сложнее вопрос стоит, когда вероятностные характеристики случайных факторов неизвестны или вообще не существуют. Такие задачи называются задачами с условиями неопределенности. Для решения задач с неопределенностью разработан специальный математический раздел «Теория игр и статистических решений». Цель теории игр - выработка рекомендаций по рациональному образу действий противоборствующих сторон в конфликтной ситуации. В игре могут сталкиваться интересы двух или более сторон преследующих разные цели. Примером может служить задача выбора лучшей технологии при производстве различной продукции. Наибольшее распространение получили парные игры.
Стратегией стороныназовем совокупность правил, определяющих выбор варианта в сложившейся ситуации (вариант действия). Оптимальная стратегия обеспечивает наилучший исход (максимальный выигрыш, минимальный проигрыш) одной из сторон.
Задача теории игр – выявление оптимальных стратегий противоборствующих сторон. При этом рассматриваются ситуации, имеющие элемент неопределенности, что отражается на достоверности окончательных решений. Самый простой случай – конечная парная игра. Допустим, что в ней участвуют две противоборствующие стороны со стратегиями А={А1,А2,…,Аn} и B={B1,B2,…,Bm}. Выигрыш стороны А является проигрышем стороны В. Обозначим исход игры a. Таким образом, сторона А, выбирая стратегию Аi(или совокупность стратегий), стремится максимизировать выигрыш а, а сторона В – минимизировать. Противопоставляя каждой стратегии Аi стратегию Вj с исходом аij игру можно представить в виде прямоугольной матрицы
| B | ||||||
| B1 | B2 | B3 | … | Bm | ||
| А | А1 | а11 | a12 | а13 | … | а1m |
| А2 | а21 | а22 | а23 | … | а2m | |
| … | … | … | … | … | … | |
| Аn | an1 | an2 | аn3 | … | аnm |
Матрицу игры изобразим кратко: ║аij║. Анализ игры проводится на основе принципа осторожности: сторона А выбирает стратегию, при которой минимальный выигрыш максимален,- «поступает так, чтобы при наихудшем для тебя поведении противоборствующей стороны получить максимальный выигрыш ». Аналогично строит свое поведение и сторона В – максимальный проигрыш должен быть минимальным.
Для реализации указанного принципа анализа матрицы конечной игры n×m устанавливаем для каждой строки αi = min αij и затем из чисел аi выбираем максимальное значение α = max αi = max min αij (α – нижняя цена игры). Для стороны В анализ проводим подобным образом. Для каждой стратегии Вj по сторонам находим максимальное значение βj = max aij, а затем из их числа выбираем минимальную величину β = min max aij (β – верхняя цена игры). В случае, если α = β, игра решается в чистых оптимальных стратегиях и называется игрой с седловой точкой. В этом случае можно указать для сторон А и В их оптимальные стратегии с исходом α = β = γ.
Если  , то гарантированный выигрыш находиться
, то гарантированный выигрыш находиться 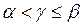 . В этом случае игра называется со смешанной стратегией.
. В этом случае игра называется со смешанной стратегией.
Чаще всего с помощью теории игр решают задачи на нахождение вероятности применения различных решений (стратегий).
В случаях α ≠ β (а эти ситуации наиболее часты) игра называется игрой со смешанными стратегиями. В оптимальном варианте необходимо найти чередование нескольких стратегий Аi и Вj.
Задача анализа в этом случае - найти частоты pi, qj (вероятности) применения стратегий Аi, Bj.
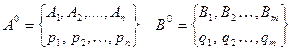
Оптимальные стратегии находим из систем уравнений:
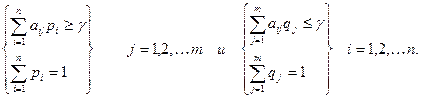 (2.16)
(2.16)
где 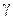 - средний гарантированный выигрыш ( α ≤
- средний гарантированный выигрыш ( α ≤ 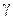 ≤ β)
≤ β)
Поделим левую и правую часть каждого из уравнений (2.16) на величину 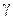 и введем новые неизвестные xi.
и введем новые неизвестные xi.
Поскольку мы стремимся максимизировать 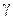 (средний гарантированный выигрыш), то
(средний гарантированный выигрыш), то 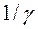 следует минимизировать. В результате выполнения таких операций мы получим новую систему которая представляет собой модель линейного программирования.
следует минимизировать. В результате выполнения таких операций мы получим новую систему которая представляет собой модель линейного программирования.
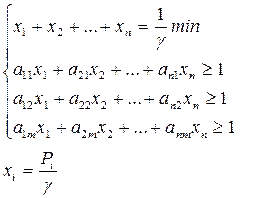
Из данной модели необходимо определить оптимальные значения 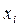 ( и соответствующие им pi ) обеспечивающие максимальный средний выйграш. Другими словами, решением этой модели будут являться величины pi, представляющие собой значения вероятности применения стратегии Аi для достижения максимального среднего выйгрыша.
( и соответствующие им pi ) обеспечивающие максимальный средний выйграш. Другими словами, решением этой модели будут являться величины pi, представляющие собой значения вероятности применения стратегии Аi для достижения максимального среднего выйгрыша.
Оптимальная стратегия поведения стороны В для достижения минимального пройгрыша (а значит для получения стороной А минимального выйгрыша) находится аналогично, но уже из системы кравнений
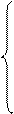
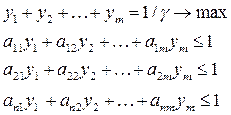
где 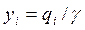
Найденные таким образом неизвестные величины qi гарантируют минимальный средний проигрыш. Значения элементов матрицы 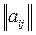 должны быть установлены предварительно.
должны быть установлены предварительно.
Принципиальное отличие методов теории статистических решений от методов теории игрзаключается в том, что рассматриваемая в ее задачах неопределенная ситуация не имеет конфликтной окраски. Таковы многие задачи прогнозирования разработки природных ресурсов, воздействия на окружающую среду, предсказания метеоусловий и др. Поэтому игры в теории статистических решений называются играми с природой, игрой статистика с природой или статистической игрой.
Пусть сторона А располагает стратегиями А1, А2 (в общем случае 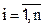 ) в условиях недостаточной информации о природе, состояния которой В1, В2,... Вm, (
) в условиях недостаточной информации о природе, состояния которой В1, В2,... Вm, ( 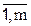 ). Исход (выигрыш или ущерб) аij (rij) заранее известен для каждой пары Аi, Вj. Кроме матрицы выигрышей (ущерба) в статистической игре могут быть известны вероятности возможных состояний природы Вj. Задача состоит в выборе оптимальной стратегии поведения стороны А. Матрица выигрышей может быть заменена на матрицу рисков
). Исход (выигрыш или ущерб) аij (rij) заранее известен для каждой пары Аi, Вj. Кроме матрицы выигрышей (ущерба) в статистической игре могут быть известны вероятности возможных состояний природы Вj. Задача состоит в выборе оптимальной стратегии поведения стороны А. Матрица выигрышей может быть заменена на матрицу рисков 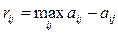
Применяются несколько критериев выбора оптимальных решений.
Например, критерий Лапласа, приписывающий всем возможным состояниям равные вероятности, более оптимистичен, чем принцип минимакса, рассчитывающий на лучший вариант среди худших исходов. Критерий Гурвица можно использовать при различных подходах - от наиболее оптимистичного до наиболее пессимистического. Перечисленные критерии, несмотря на их количественную природу, отражают субъективную оценку ситуации, в которой приходится принимать решение. К сожалению, не существует общих правил оценки применимости того или иного критерия, так как поведение (часто меняющееся) лица, принимающего решение, обусловленное неопределённостью ситуации, по всей видимости, является наиболее важным фактором при выборе подходящего критерия.
Все критерии, перечисленные выше, базируются на том, что лицу (группе лиц), принимающему решение, не противостоит разумный противник. Когда в роли противника выступает «природа», нет оснований предполагать, что она стремится причинить вред лицу, принимающему решение.
Согласно максиминному критерию Ваальда в качестве оптимальной выбирается стратегия Аi, при которой минимальный выигрыш по Вj максимален по Аi, то есть
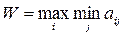
Критерий Ваальда ориентирует принимающего решение на получение максимального выигрыша в худших условиях. В связи с этим его называют критерием крайнего пессимизма.
Следующий критерий Сэвиджа рекомендует в условиях неопределенности выбирать ту стратегию, при которой величина риска принимает наименьшую величину в самой неблагоприятной обстановке, то есть: 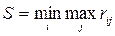
Критерий пессимизма-оптимизма Гурвица рекомендует при выборе решения в условиях неопределенности не руководствоваться ни крайним пессимизмом, ни крайним оптимизмом. Он имеет вид:
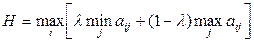 ,
,
где 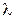 - коэффициент, выбираемый субъективно из интервала между 0 и 1. При
- коэффициент, выбираемый субъективно из интервала между 0 и 1. При 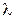 = 0 критерий Н превращается в критерий крайнего оптимизма, а при
= 0 критерий Н превращается в критерий крайнего оптимизма, а при 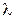 =1 - крайнего пессимизма. Задача принимающего решение - выбрать
=1 - крайнего пессимизма. Задача принимающего решение - выбрать 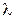 сообразно содержанию задачи. Ситуацию целесообразно анализировать с разных позиций, и если рекомендации со всех позиций совпадают, то это подтверждает правильность принимаемого решения. Если же рекомендации противоречивы, то окончательное решение следует принимать с учетом слабых и сильных сторон оптимистического и пессимистического подходов.
сообразно содержанию задачи. Ситуацию целесообразно анализировать с разных позиций, и если рекомендации со всех позиций совпадают, то это подтверждает правильность принимаемого решения. Если же рекомендации противоречивы, то окончательное решение следует принимать с учетом слабых и сильных сторон оптимистического и пессимистического подходов.
В том случае, когда неопределенность Вj характеризуется вероятностью qi , при принятии решения стремятся выбрать ту стратегию, которая дает максимум для среднего выигрыша
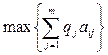
или минимум среднего риска
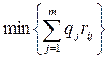
В случае, когда исход от стратегии Аi при одном и том же состоянии Вj имеет вероятностный характер, число возможных стратегий следует увеличить.
Таким образом, метод статистических решений рассматривает задачи с неопределенностью и это подчеркивает важность его в задачах прогнозирования и как следствие использование в компьютерных моделях.
Примеры практического использования теории игр (метода статистических решений)
Метод игр может быть использован для выбора наилучшего варианта сооружения или реконструкции шламохранилища. Поскольку вышеуказанная задача многокритериальная (несколько элементов Сi системы, каждый из которых может быть выбран в качестве самостоятельного критерия безопасности) и решение принимается в условиях определённости, то для её решения можно использовать метод игр и статистических решений.
В условиях неопределённости используются критерии Лапласа, Гурвица, Сэвиджа, минимакса. Основное различие между указанными критериями определяется стратегией лица, принимающего решение в условиях большой неопределённости.
Данные, необходимые для принятия решений в условиях неопределённости, обычно задают в форме матрицы, строки которой соответствуют возможным действиям, а столбцы - возможным состояниям системы. Каждому действию Аi и каждому возможному состоянию Вj соответствует результат (исход), определяющий выигрыш аij (или потери rij) при выборе данного действия и реализации данного состояния.
Рассмотрим несколько вариантов принятия решений в условиях неопределённости. Сторона А, принимающая решение, имеет две стратегии:
А1 - заниженная оценка безопасности системы (это реализация принципа осторожности, пессимизма). Обычно это лучший образ действия (принцип максимина, критерий Ваальда, Сэвиджа);
А2 - завышенная оценка безопасности системы (это оптимизм при анализе факторов, влияющих на безопасность).
Сторона В характеризуется двумя состояниями :
В1 - безаварийное и В2 - аварийное. Затраты на обеспечение в поддержание безаварийного состояния или на преодоление последствий аварии изменяются в пределах от Сmin до Сmах Эти величины можно пронормировать:
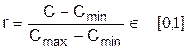 .
.
Все элементы матрицы rij можно взять в долях единицы. После умножения всех элементов .матрицы на 10 получим rij ≤ 10 .
В рассмотренной ситуации матрица игры может быть записана в виде
Таблица 3.1
| B | |||
| B1 | B2 | ||
| A | A1 | r11 | r12 |
| A2 | r21 | r22 |
В таблице 3.1 можно допустить (экспертная оценка) в первом случае r22 > r21, r22 > r11, r11 < r12 < r21. В оценочных цифрах (можно рассмотреть, как это сделано ниже, различные варианты) матрица игр имеет вид:
Таблица 3.2
| B | α | |||
| B1 | B2 | |||
| A | A1 | |||
| A2 | ||||
| β |
Методы решения игр изложены в специальной литературе [19] и поэтому здесь не рассматриваются.
Находим нижнюю цену игры:
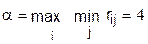
и верхнюю цену игры:
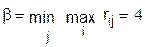
Это игра в чистых стратегиях, которая рекомендует использовать а1 (заниженную оценку безопасности) и ориентирует на безаварийную эксплуатацию объекта.
Во втором варианте принятия решений можно рассмотреть ситуацию, когда : r22 > r11 > r12> r21
Матрица игры в этом варианте имеет вид:
Таблица 3.3
| B | α | |||
| B1 | B2 | |||
| A | A1 | |||
| A2 | ||||
| β |
По данным таблицы 3.3 нижняя цена игры:
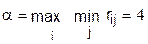
и верхняя цена игры:
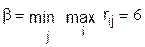
В данной ситуации α < β и , следовательно, решение может быть смешанным:
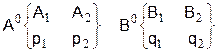
p1+p2=1 q1+q2=1
Здесь рi и qj- частоты (вероятности) использования стратегий Аi и Вj для нахождения средних потерь 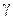 (α ≤
(α ≤ 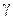 ≤ β) и pi, qj необходимо решить системы уравнений:
≤ β) и pi, qj необходимо решить системы уравнений:
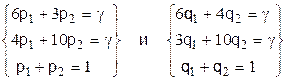
Из первой системы уравнений находим:
6р1+3(1-р1)=4р1+10(1-р1).
Откуда р1=0,78 и р2=0,22; 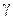 = 5,33 ( α<
= 5,33 ( α< 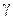 < β ) .
< β ) .
Из второй системы уравнений получим:
6q1+4(1-q1)=Зq1+10(1-q1).
Откуда q1=0,67 , q2=0,33 , 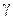 = 5,33.
= 5,33.
Таким образом, в рассмотренном случае оптимальный образ действий может быть записан как:
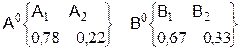
Предпочтение, хотя и не безоговорочно, и в этой ситуации отдаётся принятию решения с заниженной оценкой безопасности (р1=0,78>р2=0,22) и ориентация также в большей степени на обеспечение безаварийной эксплуатации шламохранилища (q1=:0,67>q2=0,33).
В связи с полученным анализом методом игр, влияние неопределённости при оценке безопасности шламохранилища, на наш взгляд, представляет интерес рассмотрение двух решений по шламохранилищам:
• А1 - строительство нового шламохранилища;
• А2 - реконструкция существующего шламохранилища.
Матрица игры для обоснования решения имеет вид (табл.3.1). В рассматриваемом случае а1 - решение по строительству нового шламохранилища, А2 - решение по реконструкции старого шламохранилища, В1 затраты на строительство или реконструкцию шламохранилища, В2-затраты на преодоление негативных последствий в случае возникновения аварии на шламохранилище.
Рассматриваются различные варианты соотношения затрат Сij при Аi и Вj. Также , как и в предыдущем случае, проведено нормирование Сij и все элементы rij умножены на 10. Допускается, что r22>r11 , r11>r12 , r11>r21 , r12<r21. Проанализированы различные варианты решений с отношениями
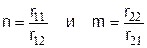
Таблица 3.4
| Варианты | |||||
| n | 1,16 | 1,14 | 1,75 | 1,8 | 2,0 |
| m | 2,5 | 2,2 | 2,0 | 1,8 | 1,5 |
Решение находилось тем же методом из принципа максимина :
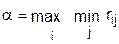 и
и 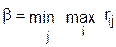
Во всех пяти вариантах имеем смешанную игру. Результаты расчётов сведены в табл. 3.5.
Таблица 3.5
 Вариант Вариант
| А | В | n | |||
| p1 | p2 | q1 | q2 | m | ||
| 0,86 | 0,14 | 0,57 | 0,43 | 6,57 | 0,464 | |
| 0,73 | 0,27 | 0,66 | 0,34 | 6,33 | 0,636 | |
| 0,625 | 0,375 | 0,75 | 0,25 | 6,25 | 0,875 | |
| 0,58 | 0,42 | 0,81 | 0,19 | 6,41 | 1,0 | |
| 0,49 | 0,51 | 0,94 | 0,06 | 6,8 | 1,33 |
Рассмотрены самые различные варианты соотношений потерь при различных вариантах сочетания Ai и Вj. Это даёт возможность проанализировать общие тенденции при обосновании решения Аi. Во-первых, во всех случаях, кроме пятого варианта, предпочтение по безопасности (риску возникновения аварии и преодоления ее. последствий) отдаётся решению по строительству нового шламохранилища. С точки зрения безопасности, это легко обосновывается (рассредоточение нагрузки, повышенная надёжность элементов сооружения, уменьшение масштабов негативного влияния экстремальных природных явлений (ураганы, бури, землетрясения). При этом учитывается высокая степень (заниженная экспертная оценка) опасности аварии и различного рода нарушений безопасности (достаточно высокое значение q2). В пятом варианте предпочтение отдаётся (с очень малым преимуществом р1=0,49 против р2=0,51) выбору решения по реконструкции старого шламохранилища. Однако, при этом следует обратить внимание, что доля влияния безопасности решения (q1=0,06) ничтожно мала по сравнению с весом затрат на реконструкцию (q1=0,94). Этот вариант имеет, на наш взгляд, не очень высокий уровень достоверности. Поэтому остаётся признать наиболее обоснованным с позиции уменьшения риска возникновения аварий на шламохранилище решение о строительстве нового сооружения.
Оптимизация на основе метода экспертных оценок. В заключение о способах решения задач с неопределенностью отметим способ экспертных оценок. Суть метода заключается в том, что проводится анкетированный опрос компетентных лиц по интересующему вопросу (проблеме), а затем полученные ответы обрабатываются статистически. Это позволяет оценить вероятность того или иного события. Опрос может проводится в несколько этапов, становясь постепенно более конкретным. Оптимальное число экспертов - 15, а число вопросов в анкете - не более 25. Таким образом, ситуация в конечном итоге сводится к принятию решений в условиях риска. Особенно часто используется метод экспертных оценок в задачах прогнозирования.
Глава 4. Разработка методов численной реализации математических моделей принятия решений с использованием подходов компьютерной математики.
§4.1 Описание и формулировка проблемы.
Как было показано в предыдущих главах, одной из основных составляющих компьютерных систем принятия решений являются оптимизационные математические модели. Предложенная теория строится на аксиомах, суть одной из которых заключается в том, что изначально задача принятия решений должна быть формализована в аналитическом виде, что позволяет наиболее полно учитывать все характерные особенности разрешаемой проблемы. Численное решение такой сложной математической задачи может быть найдено на основе специально разработанных алгоритмов, использующих аналитические, информационные и интуитивные эвристические модели. Поэтому одной из важнейших проблем построения компьютерных моделей принятия решений является разработка алгоритмов численной реализации вышеназванных математических моделей. На основании этих алгоритмов строятся алгоритмы программирования и разрабатываются компьютерные программы для вычисления оптимальных значений параметров, характеризующих принятые решения. В большинстве случаев возникает необходимость в разработке, достаточно сложных, оригинальных алгоритмов численной реализации моделей. Для численной реализации оригинальных алгоритмов возникает необходимость разработки специальных компьютерных программ.
Разработка специальной прикладной компьютерной программы представляет собой самостоятельную сложную, трудоемкую и дорогостоящую инженерную задачу. Для реализации этой задачи необходимо привлечение для совместной работы специалистов различного профиля: инженеров-производственников, исследователей, математиков-аналитиков, инженеров-программистов. Для разработки программы необходимы значительные финансовые затраты, зачастую в разы превышающие затраты на разработку самой математической модели. Следует отметить также необходимость значительных временных затрат на создание программы. Поэтому работы по созданию специальных компьютерных программ не всегда завершаются успешно, и как следствие не удается провести численное обоснование достоверности и адекватности модели. Работы по созданию математической модели в таких случаях ограничиваются, лишь, ее формализацией и описанием предполагаемого алгоритма ее численной реализации.
В предыдущей главе рассмотрены наиболее общие вопросы построения алгоритма численной реализации формализованных математических задач принятия оптимальных решений. Этот алгоритм назван интеграционной математической моделью. Его численная реализация предполагается с использованием современных вычислительных средств. Суть алгоритма заключается в последовательном введении в процесс поиска решения дополнительной информации о неизвестных и сведению, за счет этого, изначально формализованной математической модели к конечному числу более простых моделей, меньшей размерности, причем таких, для которых известен алгоритм их численной реализации. Предполагается, что этот алгоритм будет реализован с использованием компьютеров, что потребует разработки специальных программ. В их состав должны входить диалоговые программы для введения результатов интуитивного моделирования, программы для реализации информационных моделей и программы для реализации упрощенной оптимизационной математической модели.
Необходимость разработки специальных программ для ЭВМ, как следует из вышеизложенного, усложняет практическое использование метода интеграционного моделирования. Вместе с тем, использование этого метода приводит к снижению размерности изначально формализованной задачи и к сужению ОДЗ параметров и независимых (оптимизируемых) переменных. Такие обстоятельства позволяют использовать подходы компьютерной математики и, во многих практически важных случаях, обойтись без разработки специальных программ для ЭВМ. Действительно, как будет показано ниже, диалоговые процедуры, также могут быть реализованы с использованием специальных пакетов прикладных компьютерных программ, таких, например, как Excel.
На основании выше изложенного можно сделать вывод о том, что разработанные математические модели будут более привлекательными для их практического применения, если они не будут требовать разработки специальных прикладных программ их численной реализации, а будут реализованы инженерами-производственниками с помощью универсальных пакетов прикладных программ, например, таких, как Excel, Mat CAD. Для практического использования таких моделей потребуется, лишь, разработка инструкций по их практическому применению. Очевидно, что для достижения такого подхода необходимо разрабатывать такие алгоритмы для численной реализации оптимизационных задач, которые позволяют применять методы компьютерной математики. Как будет показана в данной главе монографии, эти алгоритмы могут быть построены на основе использования численных методов в задачах моделирования. Их использование приобретает все большую популярность в наше время, время бурного развития информационных технологий и, как следствие, доступности высокопроизводительных вычислительных средств. В свою очередь, из вышеизложенного следует, что одним из возможных способов развития методов компьютерной математики является предложенный в данной монографии синтез численных методов, специальных пакетов программ (таких, как Excel, Mat CAD) и метода интеграционного моделирования. Исследованию этой проблемы посвящены материалы, представленные в данной главе.
| <== предыдущая страница | | | следующая страница ==> |
| Методы нелинейного программирования и статистического анализа | | | Выбор метода численного решения многокритериальных задач |
Дата добавления: 2014-08-04; просмотров: 786; Нарушение авторских прав

Мы поможем в написании ваших работ!