Критерий совместности системы. Ранг системы.

Date: 2015-10-07; view: 504.

Общая характеристика. Метод Гаусса решения систем.

Системы линейных уравнений.

Решение систем линейных уравнений – наиболее часто встречающаяся задача вычислительной математики в инженерной практике. К этой задаче сводятся или ею сопровождаются процедуры анализа и синтеза физических систем, химических процессов и составов различной природы: электрических, механических, гидравлических и т.п. Она играет важную роль во многих разделах современной науки и техники. Даже если исследуемая система нелинейна, то она сводится к решению систем линеаразованных уравнению и последующему их численному анализу.

Пусть дана система m линейных алгебраических уравнений с n неизвестными x₁, x₂, ..., x_n и данными в правых частях свободными членами b₁, b₂, …, b_m:

(1).

В матричной форме эта система имеет вид: A· = , где =(x₁, x₂, ..., x_n), =(b₁, b₂, …, b_m) – столбцы и A=A_mхn=(a_ij) - матрица коэффициентов, называемая основной матрицей системы (1).

Если ≠ , то системы (1) называется неоднородной, в противном случае, когда b₁=b₂=…=b_m=0, называется однородной.

Решением системы(1) называется совокупность n значений неизвестных х₁=α₁, х₂=α₂, …, x_n=α_n то есть вектор (x₁, x₂, ..., x_n)=(α₁, α₂, …, α_n), при подстановке которых в систему все уравнения обращаются в верные равенства (тождества).

Система, имеющая хотя бы одно решение, называется совместной, не имеющая ни одного решения – несовместной. Система, имеющая единственное решение, называется определенной, имеющая более одного решения – неопределенной.

Две системы линейных уравнений относительно одних и тех же неизвестных называются эквивалентными, если каждое решение одной системы является решением другой системы или обе они несовместны.

Общий способ решения систем может быть основан на последовательном преобразовании системы (1) к такой эквивалентной системе, для которой решение находится достаточно просто. Мы опишем сейчас один из этих способов, называемый методом последовательного исключения неизвестных или методом Гаусса, который уже использовался для вычисления определителей и обращения матриц.

Применение вычислительных машин позволяет решать системы уравнений с большим числом неизвестных. Для этой цели разработаны высокоэффективные алгоритмы и программы.

Преобразования, которые оставляют множество решений системы (1) неизменным, то есть приводят к эквивалентной системе, следующие:

1) перестановка местами любых двух уравнений системы;

2) умножение, какого – либо из уравнений системы на число R≠0;

3) прибавление, к какому – либо уравнению другого уравнения, умноженного на произвольное постоянное число.

Указанные три преобразования системы являются элементарными преобразованиями над строками расширенной матрицы системы(А│В), где к основной матрице А добавлен через черту вектор–столбец свободных членов. Всегда можно, применяя подходящим образом элементарные операции над системой уравнений (1) или, что все равно, над расширенной матрицей (А│В) добиться либо решения заданной системы, либо прийти к явно противоречивой системе в процессе решения.

Предположим, что среди коэффициентов в левых частях уравнений есть отличные от нуля. Поменяв, если нужно, некоторые из уравнений местами и перенумеровав неизвестные (переставив столбцы), можно добиться того, чтобы коэффициент а₁₁ был не равен нулю. Прибавим теперь первое уравнение (строку матрицы), умноженное на , ко второму уравнению (строке), затем, умноженное на , к третьему, умноженное на , - к m–ому уравнению, исключим неизвестное х₁, из остальных m–1 уравнений. При проведении преобразований в случае получения уравнения вида 0·x₁+0·x₂+...+0·x_n=0, которое справедливо при любых значениях x₁, x₂, ..., x_n, мы его исключаем из системы. Если же уравнение примет вид 0·x₁+0·x₂+0·x_n=γ, где γ≠0 , то, очевидно, оно не выполняется ни для каких значений x₁, x₂, ..., x_n, и система уравнений, соответственно, не имеет решения.

Идея последовательного исключения неизвестных нашла свое воплощение в алгоритме Гаусса. Он сводится к преобразованию коэффициентов к нулю последовательно в каждом столбце расширенной матрицы (А│В) ниже главной диагонали и приведению ее к эквивалентной матрице в форме верхней треугольной или ступенчатой:

~

~

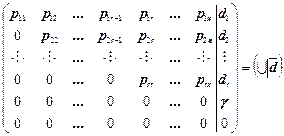
Из последней матрицы, эквивалентной первоначальной, легко находится ранг r₀ (число ненулевых строк) основной матрицыr₀=r(A)=r(U) и ранг r_p расширенной матрицы r_p= =r(A│ )=r(U│ ).

Это позволяет дать простое и эффективное условие (критерий) совместности системы линейных уравнений (1).

Теорема 1. (Кронекер и Капелли). Система (1) имеет хотя бы одно решение (совместна) в том и только в том случае, когда ранг основной матрицы системы равен рангу расширенной:r₀=r_p.

В случае их совпадения число r=r₀=r_p называется рангом системы (1); он показывает количество линейно независимых уравнений в системе (1).

Для доказательства перепишем систему (1), пользуясь определением операций со столбцами. Мы получим:

(3).

1) Если существует решение (x₁, x₂, ..., x_n ), то запись (3) означает, что столбец членов есть линейная комбинация столбцов матрицы системы. Значит, добавление этого столбца не увеличивает общего числа линейно независимых столбцов и r(A│ )=r(A), r_p=r₀=r.

2) Допустим теперь, что матрицы А и (А│ ) имеют одинаковый ранг r, и покажем, что система (1) совместна. Рассмотрим r базисных линейно независимых столбцов матрицы А; они будут базисными столбцами и расширенной матрицы (A│ ). Тогда все остальные столбцы, включая последний , матрицы (A│ ) есть линейная комбинация r базисных столбцов. Следовательно, столбец есть линейная комбинация всех столбцов матрицы А. Если мы коэффициенты этой последней комбинации обозначим через α₁, α₂, …, α_n, то получим, что выполняются равенства

.

Таким образом, система (1) удовлетворяется значениями x₁=α₁, x₂=α₂, ..., x_n=α_n и, значит, совместна.

Пример 1. Выяснить совместимость систем:

а) , б) .

а) выпишем расширенную матрицу системы и приведем ее элементарными преобразованиями к треугольному виду (прямой ход алгоритма Гаусса):

= .

Ранг основной матрицы r₀=r(A)=r(U)=2, ранг расширенной r_p=r(A│ )=r(U│ )=3. Так как r_p<r₀, то система не имеет решения.

По–другому, если записать уравнением последнюю строку преобразованной матрицы 0·x₁, 0·x₂, ..., 0·x_n=1, то в ней свободный член равен единице, а коэффициенты при неизвестных равны нулю, поэтому система несовместна.

б). Имеем прямой ход:

Ранг основной матрицы r₀=r(A)=r(U)=2 равен рангу расширенной r_p=r(A│ )=r(U│ )=2, значит, система совместна и ранг системы r=2.

Получим решение системы (обратный ход алгоритма Гаусса). Из последней строки матрицы (U│ ) находим 0·х₁=0·х₂+1·х₃=0, х₃=0. Распишем первую строку х₁+х₂+х₃=1 и подставим в нее значение х₃=0, получим х₁+х₂=1. Полагая х₁=α - любое число (-∞<α<+∞), находим х₂=1-α. Отсюда система имеет бесчисленное множество решений (х₁, х₂, х₃)=(α, 1-α, 0), где α - произвольное число. Подставив в уравнение найденные значения неизвестных, можно убедиться в этом.

Рассмотрим другой подход. Пусть системе (1) отвечает линейное отображение =А n-мерного векторного пространства Xⁿ в m–мерное векторное пространство Y^m с матрицей А относительно данных базисов. Отображение А ставит в соответствие пространству Xⁿ подпространство образов A(Xⁿ)ÌY^m, размерность которого равна рангу матрицы А, dimA(Xⁿ)=r(A)=r. Таким образом, нужно найти вектор ÎХⁿ такой, что A = где ÎY^m – данный вектор, отвечающий вектору из арифметического пространства A^m.

1. Если ÏА(Xⁿ), что возможно при r<m, то решения не существует.

2.Если ÎA(Xⁿ), то возможны только два варианта:

1) если r=n (совпадает с числом неизвестных n), то отображение А взаимно однозначно и решение единственно: =A^-1 , в матричной форме: =A^-1· ;

2) если r<n, то нужно рассмотреть (n–r) – мерное ядро – подпространство HÌXⁿ отображаемое А в нуль вектор; тогда существует бесконечно много решений вида + , где – одно из решений, а – произвольный вектор подпространства Н (A( + )=A +A = + = ).