
Supersymmetry breaking and dark energy
Date: 2015-10-07; view: 606.
Given R-parity conservation, the identity of the LSP has great cosmological importance. The gauge hierarchy problem is no help in identifying the LSP, as it may be solved with any superpartner masses, provided they are all of the order of the weak scale. What is required is an understanding of supersymmetry breaking, which governs the soft supersymmetry-breaking terms and the superpartner spectrum.
The topic of supersymmetry breaking is technical and large. However, the most popular models have “hidden sector” supersymmetry breaking, and their essential features may be understood by analogy to electroweak symmetry breaking in the standard model.
The interactions of the standard model may be divided into three sectors (see Fig. 4). The electroweak symmetry breaking (EWSB) sector contains interactions involving only the Higgs boson (the Higgs potential); the observable sector contains interactions involving only what we might call the “observable fields,” such as quarks q and leptons l; and the mediation sector contains all remaining interactions, which couple the Higgs and observable fields (the Yukawa interactions). Electroweak symmetry is broken in the EWSB sector when the Higgs boson obtains a non-zero vev: h → v. This is transmitted to the observable sector by the mediating interactions. The EWSB sector determines the overall scale of EWSB, but the interactions of the mediating sector determine the detailed spectrum of the observed particles, as well as much of their phenomenology.


Fig. 4. Sectors of interactions for electroweak symmetry breaking in the standard model and supersymmetry breaking in hidden sector supersymmetry breaking models.

Models with hidden sector supersymmetry breaking have a similar structure. They have a supersymmetry breaking sector, which contains interactions involving only fields Z that are not part of the standard model; an observable sector, which contains all interactions involving only standard model fields and their superpartners; and a mediation sector, which contains all remaining interactions coupling fields Z to the standard model. Supersymmetry is broken in the supersymmetry breaking sector when one or more of the Z fields obtains a non-zero vev: Z → F. This is then transmitted to the observable fields through the mediating interactions. In contrast to the case of EWSB, the supersymmetry-breaking vev F has mass dimension 2. (It is the vev of the auxiliary field of the Z supermultiplet.)
In simple cases where only one non-zero F vev develops, the gravitino mass is

| (8) |
where M  ≡ (8πGN)−1/2
≡ (8πGN)−1/2  2.4 × 1018 GeV is the reduced Planck mass. The standard model superpartner masses are determined through the mediating interactions by terms such as
2.4 × 1018 GeV is the reduced Planck mass. The standard model superpartner masses are determined through the mediating interactions by terms such as

| (9) |
where cij and ca are constants,  and λa are superpartners of standard model fermions and gauge bosons, respectively, and Mm is the mass scale of the mediating interactions. When Z → F, these terms become mass terms for sfermions and gauginos. Assuming order one constants,
and λa are superpartners of standard model fermions and gauge bosons, respectively, and Mm is the mass scale of the mediating interactions. When Z → F, these terms become mass terms for sfermions and gauginos. Assuming order one constants,

| (10) |
In supergravity models, the mediating interactions are gravitational, and so Mm 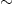 M
M  . We then have
. We then have

| (11) |
and  . In such models with “high-scale” supersymmetry breaking, the gravitino or any standard model superpartner could in principle be the LSP. In contrast, in “low-scale” supersymmetry breaking models with Mm
. In such models with “high-scale” supersymmetry breaking, the gravitino or any standard model superpartner could in principle be the LSP. In contrast, in “low-scale” supersymmetry breaking models with Mm  M
M  , such as gauge-mediated supersymmetry breaking models,
, such as gauge-mediated supersymmetry breaking models,

| (12) |
 , and the gravitino is necessarily the LSP.
, and the gravitino is necessarily the LSP.
As with electroweak symmetry breaking, the dynamics of supersymmetry breaking contributes to the energy density of the vacuum, that is, to dark energy. In non-supersymmetric theories, the vacuum energy density is presumably naturally  instead of its measured value
instead of its measured value 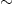 meV4, a discrepancy of 10120. This is the cosmological constant problem. In supersymmetric theories, the vacuum energy density is naturally F2. For high-scale supersymmetry breaking, one finds
meV4, a discrepancy of 10120. This is the cosmological constant problem. In supersymmetric theories, the vacuum energy density is naturally F2. For high-scale supersymmetry breaking, one finds  , reducing the discrepancy to 1090. Lowering the supersymmetry breaking scale as much as possible to
, reducing the discrepancy to 1090. Lowering the supersymmetry breaking scale as much as possible to  gives
gives  , still a factor of 1060 too big. Supersymmetry therefore eliminates from 1/4 to 1/2 of the fine-tuning in the cosmological constant, a truly underwhelming achievement. One must look deeper for insights about dark energy and a solution to the cosmological constant problem.
, still a factor of 1060 too big. Supersymmetry therefore eliminates from 1/4 to 1/2 of the fine-tuning in the cosmological constant, a truly underwhelming achievement. One must look deeper for insights about dark energy and a solution to the cosmological constant problem.
| <== previous lecture | | | next lecture ==> |
| The neutral supersymmetric spectrum | | | Minimal supergravity |