
Minimal supergravity
Date: 2015-10-07; view: 602.
To obtain detailed information regarding the superpartner spectrum, one must turn to specific models. These are motivated by the expectation that the weak-scale supersymmetric theory is derived from a more fundamental framework, such as a grand unified theory or string theory, at smaller length scales. This more fundamental theory should be highly structured for at least two reasons. First, unstructured theories lead to violations of low energy constraints, such as bounds on flavor-changing neutral currents and CP-violation in the kaon system and in electric dipole moments. Second, the gauge coupling constants unify at high energies in supersymmetric theories [5], and a more fundamental theory should explain this.
From this viewpoint, the many parameters of weak-scale supersymmetry should be derived from a few parameters defined at smaller length scales through renormalization group evolution. Minimal supergravity [6], [7], [8], [9] and [10], the canonical model for studies of supersymmetry phenomenology and cosmology, is defined by five parameters:

| (13) |
where the most important parameters are the universal scalar mass m0 and the universal gaugino mass M1/2, both defined at the grand unified scale MGUT  2 × 1016 GeV. In fact, there is a sixth free parameter, the gravitino mass
2 × 1016 GeV. In fact, there is a sixth free parameter, the gravitino mass
| m3/2. | (14) |
As noted in Section 2.5, the gravitino may naturally be the LSP. It may play an important cosmological role, as we will see in Section 4. For now, however, we follow most of the literature and assume the gravitino is heavy and so irrelevant for most discussions.
The renormalization group evolution of supersymmetry parameters is shown in Fig. 5 for a particular point in minimal supergravity parameter space. This figure illustrates several key features that hold more generally. First, as superpartner masses evolve from MGUT to Mweak, gauge couplings increase these parameters, while Yukawa couplings decrease them. At the weak scale, colored particles are therefore expected to be heavy, and unlikely to be the LSP. The Bino is typically the lightest gaugino, and the right-handed sleptons (more specifically, the right-handed stau  ) are typically the lightest scalars.
) are typically the lightest scalars.

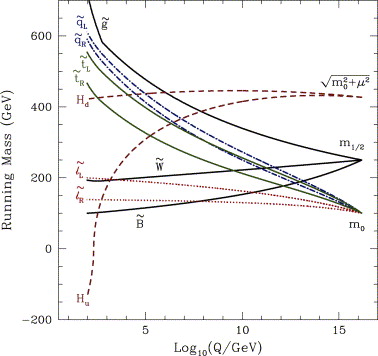
Fig. 5. Renormalization group evolution of supersymmetric mass parameters. From [11].

Second, the mass parameter  is typically driven negative by the large top Yukawa coupling. This is a requirement for electroweak symmetry breaking: at tree-level, minimization of the electroweak potential at the weak scale requires
is typically driven negative by the large top Yukawa coupling. This is a requirement for electroweak symmetry breaking: at tree-level, minimization of the electroweak potential at the weak scale requires

| (15) |
where the last line follows for all but the lowest values of tan β, which are phenomenologically disfavored anyway. Clearly, this equation can only be satisfied if  . This property of evolving to negative values is unique to
. This property of evolving to negative values is unique to  ; all other mass parameters that are significantly diminished by the top Yukawa coupling also experience a compensating enhancement from the strong gauge coupling. This behavior naturally explains why SU(2) is broken while the other gauge symmetries are not. It is a beautiful feature of supersymmetry derived from a simple high energy framework and lends credibility to the extrapolation of parameters all the way up to a large mass scale like MGUT.
; all other mass parameters that are significantly diminished by the top Yukawa coupling also experience a compensating enhancement from the strong gauge coupling. This behavior naturally explains why SU(2) is broken while the other gauge symmetries are not. It is a beautiful feature of supersymmetry derived from a simple high energy framework and lends credibility to the extrapolation of parameters all the way up to a large mass scale like MGUT.
Given a particular high energy framework, one may then scan parameter space to determine what possibilities exist for the LSP. The results for a slice through minimal supergravity parameter space are shown in Fig. 6. They are not surprising. The LSP is either the the lightest neutralino χ or the right-handed stau  . In the χ LSP case, contours of gaugino-ness
. In the χ LSP case, contours of gaugino-ness

| (16) |
where

| (17) |
are also shown. The neutralino is nearly pure Bino in much of parameter space, but may have a significant Higgsino mixture for m0 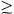 1 TeV, where Eq. (15) implies |μ|
1 TeV, where Eq. (15) implies |μ| 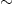 M1.
M1.


Fig. 6. Regions of the (m0, M1/2) parameter space in minimal supergravity with A0 = 0, tanβ=10, and μ > 0. The lower shaded region is excluded by the LEP chargino mass limit. The stau is the LSP in the narrow upper shaded region. In the rest of parameter space, the LSP is the lightest neutralino, and contours of its gaugino-ness Rχ (in percent) are shown. From [12].

There are, of course, many other models besides minimal supergravity. Phenomena that do not occur in minimal supergravity may very well occur or even be generic in other supersymmetric frameworks. On the other hand, if one looks hard enough, minimal supergravity contains a wide variety of dark matter possibilities, and it will serve as a useful framework for illustrating many points below.
| <== previous lecture | | | next lecture ==> |
| Supersymmetry breaking and dark energy | | | Neutralino cosmology |