
Introduction
Date: 2015-10-07; view: 801.
Quantum physics is largely governed by the Schroedinger equation. Yet, exact solutions of the equation are relatively few. Besides lattice and other numerical calculations, we rely mostly on perturbative expansions. Such expansion quite often leads to a divergent series with zero radius of convergence, as in quantum electrodynamics, quantum chromodynamics, and problems involving tunneling and instantons. In a series of previous papers [1], [2], [3] and [4] we have presented a new approach to solve the low lying states of the Schroedinger equation. In the special case of one-dimensional problems, this new approach leads to explicit convergent iterative solutions, in contrast to perturbative series expansions. These convergent solutions include the long standing difficult problem [5], [6], [7], [8], [9], [10], [11], [12], [13] and [14] of a quartic potential with symmetric minima.
In this paper, we discuss some additional results bearing on the new method. In the one-dimensional case, we show that by changing the boundary condition to be applied at each iteration, we can obtain a convergent alternating sequence for the ground state energy and wave function instead of the monotonic sequence found before [4]. This result will be spelled out later in this section and proved in Section 3. We also find that the asymmetric quartic double-well potential can be treated by an extension of the procedure used previously for the symmetric case. This extension is treated in Section 4.
In addition, we have begun the exploration of higher dimensional problems along the same line. Although the same kind of iterative procedure can be set up, the linear inhomogeneous equation to be solved at each step cannot now be reduced to simple quadratures, as was done for one dimension. However, it is of interest that this equation is identical in form to an electrostatic analog problem with a given position-dependent dielectric constant media; at each nth iteration, there is an external electrostatic charge distribution determined by the (n − 1)th iterated solution, as we shall discuss in this section.
Consider the Schroedinger equation
| Hψ=Eψ, | (1.1) |
where H is the Hamiltonian operator, ψ the wave function, and E its energy. For different physics problems, H assumes different forms. For example, for a system of n non-relativistic particles in three dimensions, H may be written as
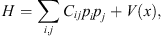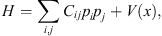
| (1.2) |
where x stands for x1, x2, … , x3n the coordinate components of these n particles, V (x) is the potential function, Cij are constants, and p1, p2, … , p3n are the momentum operators satisfying the commutation relation
| [pi,xj]=-iδij. | (1.3) |
(Throughout the paper, we set Planck's constant 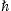 = 1.) For a relativistic field theory, the Hamiltonian usually takes on a different form. Let Φ (r) be a scalar boson field at a three-dimensional position vector r, and Π (r) be the corresponding conjugate momentum operator. In this case we may write
= 1.) For a relativistic field theory, the Hamiltonian usually takes on a different form. Let Φ (r) be a scalar boson field at a three-dimensional position vector r, and Π (r) be the corresponding conjugate momentum operator. In this case we may write
| H=∫d3r[Π2(r)+V(Φ(r))] | (1.4) |
with Π (r) and Φ (r′) satisfying the commutation relation
| [Π(r),Φ(r′)]=-iδ3(r-r′). | (1.5) |
In both cases, the dependence of H on the momentum operators pi and Π (r) are quadratic. Consequently, they can be brought into an identical standard form. In the above case of a system of non-relativistic particles, through a linear transformation
| {xi}→{qi}, | (1.6) |
the Hamiltonian (1.2) can be written in the standard form
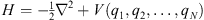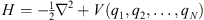
| (1.7) |
with
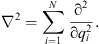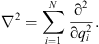
| (1.8) |
Likewise for the relativistic boson field Hamiltonian (1.4), we can use the Fourier-components of Φ (r) and Π (r) as the set {xi} and {pi}. Through a similar transformation (1.6), the field Hamiltonian (1.4) can also be brought into the standard form Figs. (1.7) and (1.8), but with the number of variables N = ∞. All our subsequent discussions will start from the Schroedinger equation in this standard form Figs. (1.7) and (1.8). Furthermore, in this paper, we shall limit our discussions only to the ground state. In order to solve
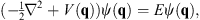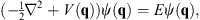
| (1.9) |
where q stands for the set {qi}, we proceed as follows:
1. Construct a good trial function  (q). A rather efficient way to find such trial functions is given in the next section.
(q). A rather efficient way to find such trial functions is given in the next section.
2. By differentiating  , we define
, we define
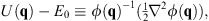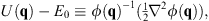
| (1.10) |
in which the constant E0 may be determined by, e.g., setting the minimum value of U (q) to be zero. Thus,  (q) satisfies a different Schroedinger equation
(q) satisfies a different Schroedinger equation

| (1.11) |
Define w (q) and 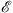 by
by
| U(q)=V(q)+w(q) | (1.12) |
and
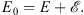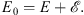
| (1.13) |
The original Schroedinger equation (1.9) can then be written as
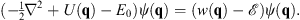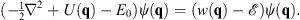
| (1.14) |
Multiplying this equation on the left by  (q) and (1.11) by ψ (q), we find their difference to be
(q) and (1.11) by ψ (q), we find their difference to be
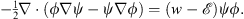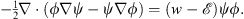
| (1.15) |
The integration of its left-hand side over all space is zero, which yields

| (1.16) |
3. The above equation (1.14) will be solved iteratively by considering the sequences
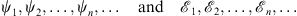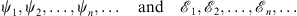
| (1.17) |
that satisfy
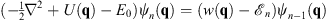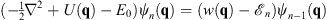
| (1.18) |
with
ψ0(q)=  (q). (q).
| (1.19) |
As in Figs. (1.15) and (1.16), we multiply (1.11) by ψn and (1.18) by  ; their difference gives
; their difference gives
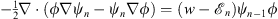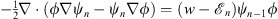
| (1.20) |
and therefore
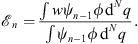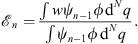
| (1.21) |
As we shall show, for many interesting problems
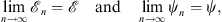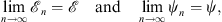
| (1.22) |
in contrast to the perturbative series expansion using w (q) as the perturbation. The key difference lies in the above expression (1.21) of 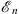 , which is a ratio, with both its numerator and denominator depending on the (n − 1)th iterative solution ψn − 1.
, which is a ratio, with both its numerator and denominator depending on the (n − 1)th iterative solution ψn − 1.
4. There exists a simple electrostatic analog problem for the iterative equation (1.18). Assuming that ψn − 1 (q) has already been solved, we can determine 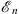 through (1.21). The right-hand side of (1.20), defined by
through (1.21). The right-hand side of (1.20), defined by
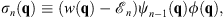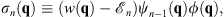
| (1.23) |
is then a known function. Introduce
fn(q)≡ψn(q)/  (q). (q).
| (1.24) |
In terms of fn (q), the nth order iterative equation (1.20) becomes
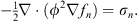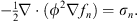
| (1.25) |
Consider a dielectric medium with a dielectric constant dependent on q, given by
κ(q)≡  2(q). 2(q).
| (1.26) |
Interpret σn (q) as the external electrostatic charge distribution, 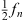 the electrostatic potential,
the electrostatic potential, 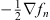 the electrostatic field, and
the electrostatic field, and
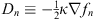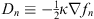
| (1.27) |
the corresponding displacement vector field. Thus (1.25) becomes
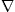 ·Dn=σn, ·Dn=σn,
| (1.28) |
the Maxwell equation for this electrostatic analog problem.
At infinity,  (∞) = 0. In accordance with Figs. (1.26) and (1.27), we also have Dn (∞) = 0. Hence the integration of (1.28) leads to the total external electrostatic charge to be also zero; i.e.,
(∞) = 0. In accordance with Figs. (1.26) and (1.27), we also have Dn (∞) = 0. Hence the integration of (1.28) leads to the total external electrostatic charge to be also zero; i.e.,
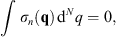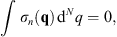
| (1.29) |
which is the same result given by (1.21) for the determination of 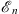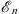 . Because the dielectric constant κ (q) in this analog problem is zero at q = ∞, the dielectric media becomes a perfect dia-electric at ∞. Thus, the equation of zero total charge, given by (1.29), may serve as a much simplified model of charge confinement, analogous to color confinement in quantum chromodynamics.
. Because the dielectric constant κ (q) in this analog problem is zero at q = ∞, the dielectric media becomes a perfect dia-electric at ∞. Thus, the equation of zero total charge, given by (1.29), may serve as a much simplified model of charge confinement, analogous to color confinement in quantum chromodynamics.
We note that (1.25) can also be derived from a minimal principle by defining
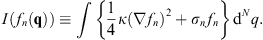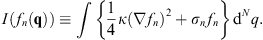
| (1.30) |
Because of (1.29), the functional I (fn (q)) is invariant under
| fn(q)→fn(q)+constant. | (1.31) |
Since the quadratic part of I (fn (q)) is the integral of the positive definite 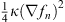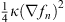 , the curvature of I (fn (q)) in the functional space fn (q) is always positive. Hence, I (fn (q)) has a minimum, and that minimum determines a unique electrostatic field
, the curvature of I (fn (q)) in the functional space fn (q) is always positive. Hence, I (fn (q)) has a minimum, and that minimum determines a unique electrostatic field 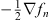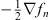 , as we shall see. To establish the uniqueness, let us assume two different
, as we shall see. To establish the uniqueness, let us assume two different 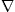 fn, both satisfy (1.25), with the same κ =
fn, both satisfy (1.25), with the same κ =  2 and the same σn; their difference would then satisfy (1.25) with a zero external charge distribution. For σn = 0, the minimum of I (fn (q)) is clearly zero with the corresponding
2 and the same σn; their difference would then satisfy (1.25) with a zero external charge distribution. For σn = 0, the minimum of I (fn (q)) is clearly zero with the corresponding 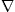 fn = 0. To derive fn (q) from
fn = 0. To derive fn (q) from 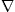 fn, there remains an additive constant at each iteration. As we shall show, this arbitrariness allows us the freedom to derive different types of convergent series.
fn, there remains an additive constant at each iteration. As we shall show, this arbitrariness allows us the freedom to derive different types of convergent series.
To illustrate this freedom, let us consider a one-dimensional problem in which we may replace the variables {qi} by a single x. Furthermore, for this discussion, let us assume the potential V (x) to be an even function, with
| V(x)=V(-x) | (1.32) |
(a condition that will be relaxed in our later analysis). The evenness of V (x) requires ψ (x) = ψ (−x) and therefore also  (x) =
(x) =  (−x). Thus, we need only to consider the half-space
(−x). Thus, we need only to consider the half-space
x  0. 0.
| (1.33) |
Eqs. Figs. (1.24), (1.27) and (1.28) can be written now as
fn(x)=ψn(x)/  (x), (x),
| (1.34) |
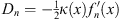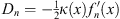
| (1.35) |
and
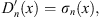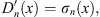
| (1.36) |
where
κ(x)=  2(x) 2(x)
| (1.37) |
and

| (1.38) |
same as before. Throughout the paper, ′ denote  .
.
From (1.36) and Dn (∞) = 0, we have
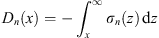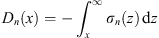
| (1.39) |
and, since σn (x) is even in x, we have from (1.29),

| (1.40) |
It follows then from (1.34) and Figs. (1.38), (1.39) and (1.40),
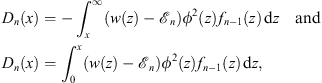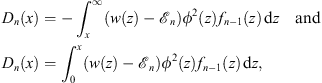
| (1.41) |
which lead to, through (1.35),
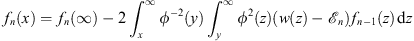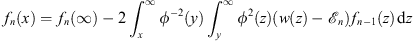
| (1.42) |
and

| (1.43) |
Consider first the case that w (x) in (1.38) is positive and satisfies
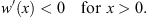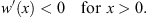
| (1.44) |
The hierarchy theorem that will be proved in Section 3 states that if w (x) satisfies (1.44) then the iterative solution of (1.42) with the boundary condition
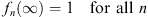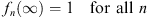
| (1.45) |
gives a convergent monotonic sequence 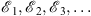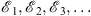 , where for all n,
, where for all n,
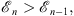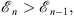
| (1.46) |
and
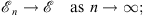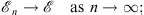
| (1.47) |
likewise, the sequence f0 (x) = 1, f1 (x), f2 (x), … is also monotonic and convergent at any x  0 with
0 with
| fn(x)>fn-1(x) | (1.48) |
and
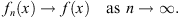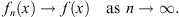
| (1.49) |
Furthermore, the convergence of Figs. (1.47) and (1.49) can hold for arbitrarily large but finite w (x). A result that is surprising, but pleasant.
On the other hand, if instead of (1.45), we impose a different boundary condition, one given by
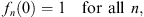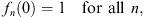
| (1.50) |
then instead of (1.47), we have for all odd n = 2m + 1 an ascending sequence
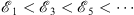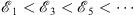
| (1.51) |
however, for the even n = 2m series, we have a descending sequence
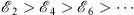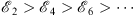
| (1.52) |
furthermore, between any even n = 2m and any odd n = 2l + 1, we have
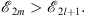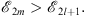
| (1.53) |
Since according to (1.13), 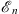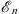 is the nth order iteration towards
is the nth order iteration towards
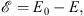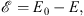
| (1.54) |
each odd member  in (1.51) gives an upper bound of E, whereas each even member
in (1.51) gives an upper bound of E, whereas each even member 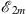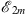 in (1.52) leads to a lower bound of E. Both sequences approach the correct
in (1.52) leads to a lower bound of E. Both sequences approach the correct  as n → ∞, one from above and the other from below. For the boundary condition (1.50), our proof of convergence requires a condition on the magnitude of w (x). Still this is quite a remarkable result.
as n → ∞, one from above and the other from below. For the boundary condition (1.50), our proof of convergence requires a condition on the magnitude of w (x). Still this is quite a remarkable result.
In Section 2, we discuss the details of how to construct a good trial function  (q) for the N-dimensional problem. Section 3 gives the proof of the hierarchy theorem for the one-dimensional problem in which V (x) = V (−x) is an even function of x and the potential-difference function w (x) is assumed to satisfy (1.44); i.e., w′ (x) < 0 for x > 0. The extension to the asymmetric case V (x) ≠ V (−x) is discussed in Section 4. The hierarchy theorem is also applicable to Mathieu's equation, which has infinite number of maxima and minima. In Appendix A, we give a soluble example in one dimension.
(q) for the N-dimensional problem. Section 3 gives the proof of the hierarchy theorem for the one-dimensional problem in which V (x) = V (−x) is an even function of x and the potential-difference function w (x) is assumed to satisfy (1.44); i.e., w′ (x) < 0 for x > 0. The extension to the asymmetric case V (x) ≠ V (−x) is discussed in Section 4. The hierarchy theorem is also applicable to Mathieu's equation, which has infinite number of maxima and minima. In Appendix A, we give a soluble example in one dimension.
In dimensions greater than 1, at each iteration Eq. (1.21) gives a fine tuning of the energy, just like the one-dimensional problem. Hence, there are good reasons to expect our approach to yield convergent solutions in any higher dimension. In Section 5, we formulate an explicit conjecture to this effect. We describe an attempt to prove this conjecture by generalizing the steps used to prove the hierarchy theorem in one dimension. The attempt fails at present because the proof of one of the lemmas does not appear to generalize in higher dimension.
The present paper represents the synthesis and generalization of results, some of which have appeared in our earlier publications [1], [2], [3] and [4]. The function Dn introduced in this paper is identical to the function hn used in [4].
| <== previous lecture | | | next lecture ==> |
| Article Outline | | | A new formulation of perturbative expansion |