
A new formulation of perturbative expansion
Date: 2015-10-07; view: 1068.
Construction of trial functions
In many problems of interest, perturbative expansion leads to asymptotic series, which is not the aim of this paper. Nevertheless, the first few terms of such an expansion could provide important insight to what a good trial function might be. For our purpose, a particularly convenient way is to follow the method developed in [1] and [2]. As we shall see, in this new method to each order of the perturbation, the wave function is always expressible in terms of a single line-integral in the N-dimensional coordinate space, which can be readily used for the construction of the trial wave function.
We begin with the Hamiltonian H in its standard form (1.7). Assume V (q) to be positive definite, and choose its minimum to be at q = 0, with
V(q) 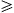 V(0)=0. V(0)=0.
| (2.1) |
Introduce a scale factor g2 by writing
| V(q)=g2v(q) | (2.2) |
and correspondingly
| ψ(q)=e-gS(q). | (2.3) |
Thus, the Schroedinger equation (1.9) becomes
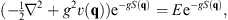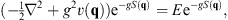
| (2.4) |
where, as before, q denotes q1, q2, … , qN and 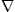 the corresponding gradient operator. Hence S (q) satisfies
the corresponding gradient operator. Hence S (q) satisfies
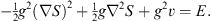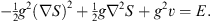
| (2.5) |
Considering the case of large g, we expand
S(q)=S0(q)+g-1S1(q)+g-2S2(q)+ 
| (2.6) |
and
E=gE0+E1+g-1E2+ 
| (2.7) |
Substituting Figs. (2.6) and (2.7) into (2.5) and equating the coefficients of g−n on both sides, we find
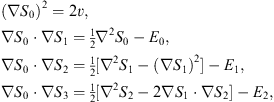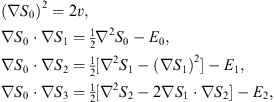
| (2.8) |
etc. In this way, the second-order partial differential equation (2.5) is reduced to a series of first-order partial differential equations (2.8). The first of this set of equations can be written as
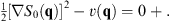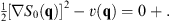
| (2.9) |
As noted in [1], this is precisely the Hamilton–Jacobi equation of a single particle with unit mass moving in a potential “−v (q)” in the N-dimensional q-space. Since q = 0 is the maximum of the classical potential energy function −v (q), for any point q ≠ 0 there is always a classical trajectory with a total energy 0+, which begins from q = 0 and ends at the other point q ≠ 0, with S0 (q) given by the corresponding classical action integral. Furthermore, S0 (q) increases along the direction of the trajectory, which can be extended beyond the selected point q ≠ 0, towards ∞. At infinity, it is easy to see that S0 (q) = ∞, and therefore the corresponding wave amplitude e-gS0(q) is zero. To solve the second equation in (2.8), we note that, in accordance with Figs. (2.1) and (2.2) at q = 0, 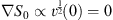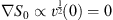 . By requiring S1 (q) to be analytic at q = 0, we determine
. By requiring S1 (q) to be analytic at q = 0, we determine
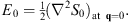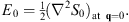
| (2.10) |
It is convenient to consider the surface
| S0(q)=constant; | (2.11) |
its normal is along the corresponding classical trajectory passing through q. Characterize each classical trajectory by the S0-value along the trajectory and a set of N − 1 angular variables
| α=(α1(q),α2(q),…,αN-1(q)), | (2.12) |
so that each α determines one classical trajectory with
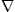 αj· αj· 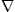 S0=0, S0=0,
| (2.13) |
where
| j=1,2,…,N-1. | (2.14) |
(As an example, we note that as q → 0, 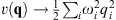 and therefore
and therefore 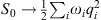 . Consider the ellipsoidal surface S0 = constant. For S0 sufficiently small, each classical trajectory is normal to this ellipsoidal surface. A convenient choice of α could be simply any N − 1 orthogonal parametric coordinates on the surface.) Each α designates one classical trajectory, and vice versa. Every (S0, α) is mapped into a unique set (q1, q2, … , qN) with S0
. Consider the ellipsoidal surface S0 = constant. For S0 sufficiently small, each classical trajectory is normal to this ellipsoidal surface. A convenient choice of α could be simply any N − 1 orthogonal parametric coordinates on the surface.) Each α designates one classical trajectory, and vice versa. Every (S0, α) is mapped into a unique set (q1, q2, … , qN) with S0 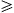 0 by construction. In what follows, we regard the points in the q-space as specified by the coordinates (S0, α). Depending on the problem, the mapping (q1, q2, … , qN) → (S0, α) may or may not be one-to-one. We note that, for q near 0, different trajectories emanating from q = 0 have to go along different directions, and therefore must associate with different α. Later on, as S0 increases each different trajectory retains its initially different α-designation; consequently, using (S0, α) as the primary coordinates, different trajectories never cross each other. The trouble-some complications of trajectory-crossing in q-space is automatically resolved by using (S0, α) as coordinates. Keeping α fixed, the set of first-order partial differential equation can be further reduced to a set of first-order ordinary differential equation, which are readily solvable, as we shall see. Write
0 by construction. In what follows, we regard the points in the q-space as specified by the coordinates (S0, α). Depending on the problem, the mapping (q1, q2, … , qN) → (S0, α) may or may not be one-to-one. We note that, for q near 0, different trajectories emanating from q = 0 have to go along different directions, and therefore must associate with different α. Later on, as S0 increases each different trajectory retains its initially different α-designation; consequently, using (S0, α) as the primary coordinates, different trajectories never cross each other. The trouble-some complications of trajectory-crossing in q-space is automatically resolved by using (S0, α) as coordinates. Keeping α fixed, the set of first-order partial differential equation can be further reduced to a set of first-order ordinary differential equation, which are readily solvable, as we shall see. Write
| S1(q)=S1(S0,α), | (2.15) |
the second line of (2.8) becomes
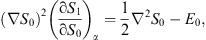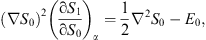
| (2.16) |
and leads to, besides (2.10), also
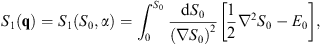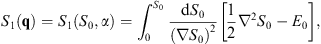
| (2.17) |
where the integration is taken along the classical trajectory of constant α. Likewise, the third, fourth, and other lines of (2.8) lead to
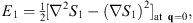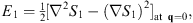
| (2.18) |
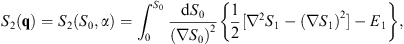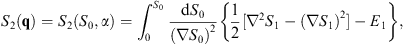
| (2.19) |
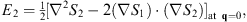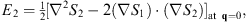
| (2.20) |
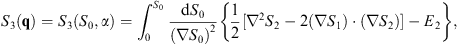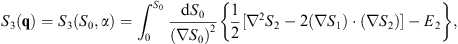
| (2.21) |
etc. These solutions give the convenient normalization convention at q = 0,
| S(0)=0 |
and
| e-S(0)=1. | (2.22) |
Remarks:
(i) As an example, consider an N-dimensional harmonic oscillator with
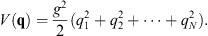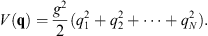
| (2.23) |
From (2.2), one sees that the Hamilton–Jacobi equation (2.9) is for a particle moving in a potential given by
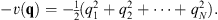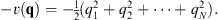
| (2.24) |
Thus, for any point q ≠ 0 the classical trajectory of interest is simply a straight line connecting the origin and the specific point, with the action
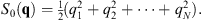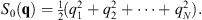
| (2.25) |
The corresponding energy is, in accordance with (2.10),
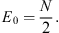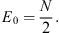
| (2.26) |
By using (2.8), one can readily show that E1 = E2 =  = 0 and S1 = S2 =
= 0 and S1 = S2 =  = 0. The result is the well-known exact answer with the ground state wave function for the Schroedinger equation (2.4) given by
= 0. The result is the well-known exact answer with the ground state wave function for the Schroedinger equation (2.4) given by
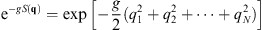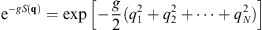
| (2.27) |
and the corresponding energy
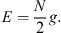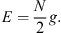
| (2.28) |
(ii) From this example, it is clear that the above expression Figs. (2.6), (2.7) and (2.8) is not the well-known WKB method. The new formalism uses −v (q) as the potential for the Hamilton–Jacobi equation, and its “classical” trajectory carries a 0+ energy; consequently, unlike the WKB method, there is no turning point along the classical trajectory, and the formalism is applicable to arbitrary dimensions.
| <== previous lecture | | | next lecture ==> |
| Introduction | | | Trial function for the quantum double-well potential |