
Symmetric vs asymmetric potential
Date: 2015-10-07; view: 607.
As we shall discuss, the general description leading from the trial function χ (x) to the final wave function ψ (x) that satisfies the Schroedinger equation (4.2) may be set in a more general framework. Decompose any potential V (x) into two parts

| (4.67) |
Next, extend the functions Va (x) and Vb (x) by defining

| (4.68) |
Thus, both Va (x) and Vb (x) are symmetric potential covering the entire x-axis. Let χa (x) and χb (x) be the ground state wave functions of the Hamiltonians T + Va and T + Vb:
| (T+Va(x))χa(x)=Eaχa(x) | (4.69a) |
and
| (T+Vb(x))χb(x)=Ebχb(x). | (4.69b) |
The symmetry (4.68) implies that

| (4.70) |
and at x = 0

| (4.71) |
Choose the relative normalization factors of χa and χb, so that at x = 0
| χa(0)=χb(0). | (4.72) |
The same trial function (4.9) for the specific quartic potential (4.1) is a special example of

| (4.73) |
with

| (4.74) |
In general, from Figs. (4.69a) and (4.69b) we see that χ (x) satisfies

| (4.75) |
Depending on the relative magnitude of Ea and Eb, we define, in the case of Ea > Eb

| (4.76a) |
and

| (4.77a) |
otherwise, if Eb > Ea, we set

| (4.76b) |
and

| (4.77b) |
Thus, we have either

| (4.78a) |
at all finite x, or

| (4.78b) |
at all finite x. A comparison between Figs. (4.9), (4.10), (4.11), (4.12), (4.13), (4.14), (4.15), (4.16) and (4.17) and (4.73)–(4.77a) shows that w (x) of (4.14) and the above  differs only by a constant.
differs only by a constant.
As in (4.2), ψ (x) is the ground state wave function that satisfies
| (T+V(x))ψ(x)=Eψ(x), | (4.79) |
which can also be written in the same form as (1.14)

| (4.80) |
with

| (4.81) |
Here, unlike (1.32), V (x) can now also be asymmetric. Taking the difference between ψ (x) times (4.75) and χ (x) times (4.80), we derive

| (4.82) |
Introduce
| ψ(x)=χ(x)f(x), | (4.83) |
in which f (x) satisfies

| (4.84) |
On account of Figs. (4.82) and (4.83), the same equation can also be written as

| (4.85) |
Eq. (4.80) will again be solved iteratively by introducing
| ψn(x)=χ(x)fn(x) | (4.86) |
with ψn and its associated energy  determined by
determined by

| (4.87) |
and
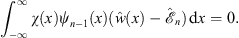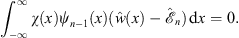
| (4.88) |
In terms of fn (x), we have

| (4.89) |
On account of (4.88), we also have

| (4.90) |
and

| (4.91) |
For definiteness, let us assume that
| Ea>Eb | (4.92) |
in Figs. (4.69a) and (4.69b); therefore  and
and  , in accordance with (4.76a). Start with, for n = 0,
, in accordance with (4.76a). Start with, for n = 0,
| f0(x)=1, | (4.93) |
we can derive {En} and {fn (x)}, with

| (4.94) |
by using the boundary conditions, either

| (4.95) |
or

| (4.96) |
It is straightforward to generalize the Hierarchy theorem to the present case. As in Section 3, in Case (A), the validity of the Hierarchy theorem imposes no condition on the magnitude of  . But in Case (B) we assume
. But in Case (B) we assume  to be not too large so that (4.91) and the boundary condition fn (−∞) = 1 is consistent with
to be not too large so that (4.91) and the boundary condition fn (−∞) = 1 is consistent with
| fn(x)>0 | (4.95) |
for all finite x. From the Hierarchy theorem, we find in Case (A)
E1>E2>E3> 
| (4.96) |
and
1  f1(x) f1(x)  f2(x) f2(x)  f3(x) f3(x)   , ,
| (4.97) |
while in Case (B)
E1>E3>E5> 
| (4.98) |
E2<E4<E6< 
| (4.99) |
1  f1(x) f1(x)  f3(x) f3(x)  f5(x) f5(x)  
| (4.100) |
and
1  f2(x) f2(x)  f4(x) f4(x)  f6(x) f6(x)   . .
| (4.101) |
A soluble model of an asymmetric square-well potential is given in Appendix A to illustrate these properties.
5. The N-dimensional problem
The N-dimensional case will be discussed in this section. We begin with the electrostatic analog introduced in Section 1. Suppose that the (n − 1)th iterative solution fn − 1 (q) is already known. The nth order charge density σn (q) is

| (5.1) |
in accordance with Figs. (1.23) and (1.24). Likewise, from Figs. (1.26) and (1.29) the dielectric constant κ of the medium is related to the trial function  (q) by
(q) by
κ(q)=  2(q) 2(q)
| (5.2) |
and the nth order energy shift 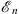 is determined by
is determined by

| (5.3) |
In the following we assume the range of w (q) to be finite, with
| w(∞)=0 | (5.4) |
and
0  w(q) w(q)  Wmax. Wmax.
| (5.5) |
Introduce

| (5.6) |
where δ (w (q) − W) is Dirac's δ-function, W is a constant parameter and the integrations in Figs. (5.3) and (5.6) are over all q-space. Similarly, for any function F (q), we define

| (5.7) |
In the N-dimensional case, the generalization of [F], introduced by (3.15), is

| (5.8) |
In terms of Fav (W), (5.8) can also be written as

| (5.9) |
Thus from Figs. (5.1) and (5.3) we have

| (5.10) |
the n-dimensional extension of (3.14).
Following Figs. (1.27) and (1.28), the nth order electric field is 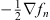 and the displacement field is
and the displacement field is

| (5.11) |
The corresponding Maxwell equation is
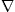 ·Dn=σn. ·Dn=σn.
| (5.12) |
Eqs. Figs. (5.11) and (5.12) determine fn except for an additive constant, which can be chosen by requiring

| (5.13) |
Therefore,
fn(q)  1. 1.
| (5.14) |
As in the one-dimensional case discussed in Section 3, (5.10) gives the same condition of fine energy tuning at each order of iteration. It is this condition that leads to convergent iterative solutions derived in Section 3. We now conjecture that

| (5.15) |
and

| (5.16) |
also hold in higher dimensions. Although we are not able to establish this conjecture, in the following we present the proofs of the N-dimensional generalizations of some of the lemmas proved in Section 3.
Lemma 1
For any pair fm(q) and fl(q) if at all W within the range (5.5),

| (5.17) |
and

| (5.18) |
Proof
For any function  , define
, define

| (5.19) |
Thus for any function F (q), we have
[F(q)]=  Fav(W) Fav(W)  ; ;
| (5.20) |
therefore,

| (5.21) |
and

| (5.22) |
By setting the subscript n in (5.10) to be m + 1, we obtain

| (5.23) |
Also by definition (5.19),
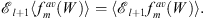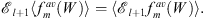
| (5.24) |
The difference of Figs. (5.23) and (5.24) gives

| (5.25) |
From (5.10) and setting the subscript n to be l + 1, we have

| (5.26) |
Regard  and
and  as two constant parameters. Multiply (5.25) by
as two constant parameters. Multiply (5.25) by  , (5.26) by
, (5.26) by  and take their difference. The result is
and take their difference. The result is

| (5.27) |
analogous to (4.43).
(i) If  , then for
, then for 

| (5.28) |
Thus, the function inside the bracket 
 in (5.21) is positive, being the product of two negative factors,
in (5.21) is positive, being the product of two negative factors,  and
and  . Also, when
. Also, when  , these two factors both reverse their signs. Consequently (5.17) holds.
, these two factors both reverse their signs. Consequently (5.17) holds.
(ii) If  , we see that for
, we see that for  , (5.28) reverses its sign, and therefore the function inside the bracket
, (5.28) reverses its sign, and therefore the function inside the bracket 
 in (5.27) is now negative. The same negative sign can be readily established for
in (5.27) is now negative. The same negative sign can be readily established for  . Consequently, (5.18) holds and Lemma 1 is established.
. Consequently, (5.18) holds and Lemma 1 is established. 
Lemma 2
Identical to Lemma 2 of Section 3.
In order to establish the N-dimensional generalization of Lemma 3 of Section 3, we define

| (5.29) |
Because of (5.3), Qn (W) is also given by

| (5.30) |
We may picture that the entire q-space is divided into two regions

| (5.31) |
and

| (5.32) |
with Qn (W) the total charge in I, which is also the negative of the total charge in II. By using Figs. (5.1) and (5.7), we see that

| (5.33) |
Lemma 3
For any pair fm (q) and fl (q) if at all W within the range (5.5)
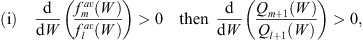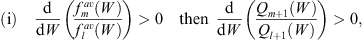
| (5.34) |

| (5.35) |
Proof
Note that Figs. (5.34) and (5.35) are very similar to Figs. (3.56) and (3.57). As in (3.60), define

| (5.36) |
From (5.33), we have

| (5.37) |
and

| (5.38) |
Therefore,

| (5.39) |
where

| (5.40) |
Furthermore,
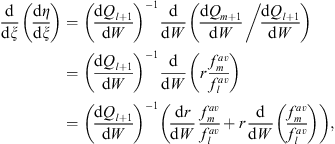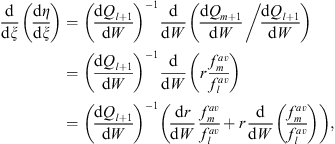
| (5.41) |
where

| (5.42) |
analogous to Figs. (3.61), (3.62), (3.63) and (3.64).
According to (5.30), at W = 0
| Qm+1(0)=Ql+1(0)=0 | (5.43) |
and according to (5.29), at W = Wmax
| Qm+1(Wmax)=Ql+1(Wmax)=0. | (5.44) |
From (5.37), we see that the derivative 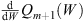 is positive when
is positive when  , zero at
, zero at  , and negative when
, and negative when  . Likewise, from (5.38),
. Likewise, from (5.38), 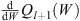 is positive when
is positive when  , zero at
, zero at  and negative when
and negative when  . Their ratio determines
. Their ratio determines  .
.
(i) If  , from Lemma 1, we have
, from Lemma 1, we have

| (5.45) |
and therefore, on account of (5.42)

| (5.46) |
At W = 0,

| (5.47) |
As W increases, so does r (W). At  , r (W) has a discontinuity, with
, r (W) has a discontinuity, with

| (5.48) |
and

| (5.49) |
As W increases from  , r (W) continues to increase, with
, r (W) continues to increase, with

| (5.50) |
and

| (5.51) |
It is convenient to divide the range 0 < W < Wmax into three regions:

| (5.52) |

| (5.53) |
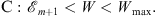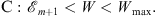
| (5.54) |
Assuming  , we shall show separately
, we shall show separately  in these three regions.
in these three regions.
In region B, Ql + 1 is decreasing, but Qm + 1 is increasing. Clearly,

| (5.55) |
In region A,  , r (W) is positive according to Figs. (5.47) and (5.48) and
, r (W) is positive according to Figs. (5.47) and (5.48) and  is always >0 from (5.46). Therefore from (5.41),
is always >0 from (5.46). Therefore from (5.41),

| (5.56) |
In region C,  , but r (W) and
, but r (W) and  are both positive. Hence,
are both positive. Hence,

| (5.57) |
Within each region, η = Qm + 1 (W) and ξ = Ql + 1 (W) are both monotonic in W; therefore η is a single-valued function of ξ and we can apply Lemma 2 of Section 3.
In region A, at W = 0 both Qm + 1 (0) and Ql + 1 (0) are 0 according to (5.43), but their ratio is given by

| (5.58) |
Therefore

| (5.59) |
Furthermore, from (5.56),  . It follows from Lemma 2 of Section 3, the ratio η/ξ is an increasing function of ξ. Since
. It follows from Lemma 2 of Section 3, the ratio η/ξ is an increasing function of ξ. Since

| (5.60) |
we also have

| (5.61) |
In region C, at W = Wmax, both Qm + 1 (Wmax) and Ql + 1 (Wmax) are 0 according to (5.44). Their ratio is

| (5.62) |
which gives at W = Wmax

| (5.63) |
As W decreases from Wmax to  in region C, since
in region C, since  , we have
, we have

| (5.64) |
Furthermore, from (5.57),  in region C. It follows from Lemma 2 of Section 3, the ratio η/ξ is a decreasing function of ξ, which together with (5.64) lead to
in region C. It follows from Lemma 2 of Section 3, the ratio η/ξ is a decreasing function of ξ, which together with (5.64) lead to

| (5.65) |
Thus, we prove Case (i) of Lemma 3. Case (ii) of Lemma 3 follows from Case (i) by an exchange of the subscripts m and l. Lemma 3 is then proved. 
So far, the above lk and lk are almost identical copies of lk and lk of Section 3, but now applicable to the N-dimensional problem. Difficulty arises when we try to generalize Lemma 4 of Section 3.
It is convenient to transform the Cartesian coordinates q1, q2, … , qN to a new set of orthogonal coordinates:
| (q1,q2,…,qN)→(w(q),β1(q),…,βN-1(q)) | (5.66) |
with
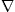 w· w· 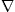 βi=0 βi=0
| (5.67) |
and
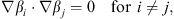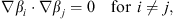
| (5.68) |
where i or j = 1, 2, … , N − 1. Introducing

| (5.69) |

| (5.70) |
In terms of the new coordinates, the components of Dn are

| (5.71) |
Its divergence is

| (5.72) |
Combining (5.12) with (5.30), we have

| (5.73) |
therefore,

| (5.74) |
in which the integration is along the surface
| w(q)=W. | (5.75) |
From Figs. (5.11) and (5.71), it follows that

| (5.76) |
In terms of curvilinear coordinates, (5.7) can be written as

| (5.77) |
Substituting (5.76) into (5.74), we find

| (5.78) |
Because  , (5.78) can also be written as
, (5.78) can also be written as

| (5.79) |
Here comes the difficulty. While the above Lemma 3 transfers relations between  to those between Qm + 1/Ql + 1, the latter is
to those between Qm + 1/Ql + 1, the latter is

| (5.80) |
which is quite different from  . This particular generalization of the lemmas in higher dimensions fails to establish the Hierarchy Theorem.
. This particular generalization of the lemmas in higher dimensions fails to establish the Hierarchy Theorem.
For the one-dimensional case discussed in Section 3, we have w′ < 0 and x  0; consequently (5.80) is
0; consequently (5.80) is  . Therefore, Lemma 4 of Section 3 can also be established by using (5.80), and the proof of the Hierarchy Theorem can be completed.
. Therefore, Lemma 4 of Section 3 can also be established by using (5.80), and the proof of the Hierarchy Theorem can be completed.

| <== previous lecture | | | next lecture ==> |
| Construction of the second trial function | | | References |