
Construction of the second trial function
Date: 2015-10-07; view: 618.
To construct the second trial function χ (x) introduced in (4.9), we define f± (x) by
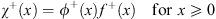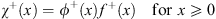
| (4.47a) |
and
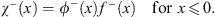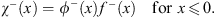
| (4.47b) |
To retain flexibility it is convenient to impose only the boundary condition (4.11) first, but not (4.10); i.e., at x = 0
| χ+′(0)=χ-′(0)=0, | (4.48) |
but leaving the choice of the overall normalization of χ+ (0) and χ− (0) to be decided later. We rewrite the Schroedinger equations Figs. (4.12) and (4.13) in their equivalent forms
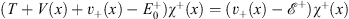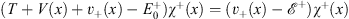
| (4.49a) |
and
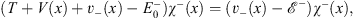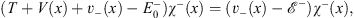
| (4.49b) |
where
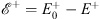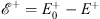
| (4.50a) |
and
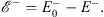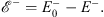
| (4.50b) |
Because at x = 0,  +′(0) =
+′(0) =  −′(0) = 0, in accordance with (4.5), we have, on account of (4.48),
−′(0) = 0, in accordance with (4.5), we have, on account of (4.48),
| f+′(0)=f-′(0)=0. | (4.51) |
So far, the overall normalization of f+ (x) and f− (x) are still free. We may choose
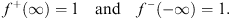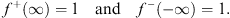
| (4.52) |
From Figs. (4.6a), (4.47a), (4.49a) and (4.50a), we see that f+ (x) satisfies the integral equation (for x  0)
0)
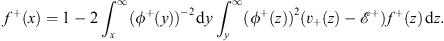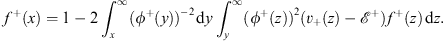
| (4.53a) |
Furthermore, from Figs. (4.6a) and (4.49a), we also have
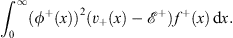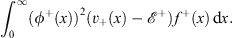
| (4.54a) |
Likewise, f− (x) satisfies (for x  0)
0)
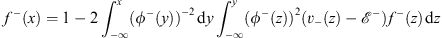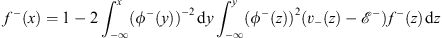
| (4.53b) |
and
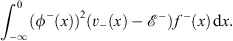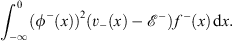
| (4.54b) |
The function f+ (x) and f− (x) will be solved through the iterative process described in Section 1. We introduce the sequences 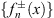 and
and 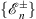 for n = 1, 2, 3, … , with
for n = 1, 2, 3, … , with
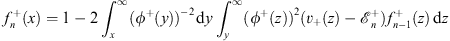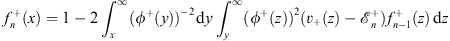
| (4.55a) |
for x  0, and
0, and
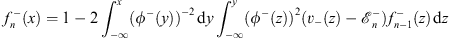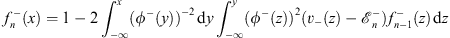
| (4.55b) |
for x  0, where
0, where 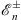 satisfies
satisfies
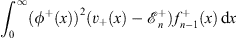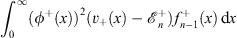
| (4.56a) |
and
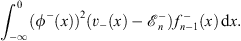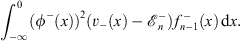
| (4.56b) |
Thus, Figs. (4.55a) and (4.55b) can also be written in their equivalent expressions
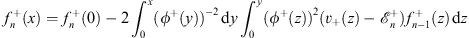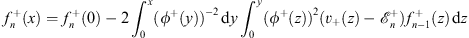
| (4.57a) |
for x  0, and
0, and
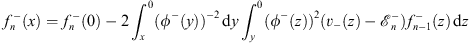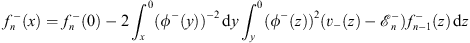
| (4.57b) |
for x  0. For n = 0, we set
0. For n = 0, we set
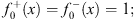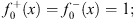
| (4.58) |
through induction and by using Figs. (4.55a), (4.55b), (4.56a) and (4.56b), we derive all subsequent 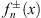 and
and 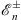 . Because v± (x) satisfies Figs. (4.44a), (4.44b) and (4.46), the Hierarchy theorem proved in Section 3 applies. The boundary conditions f+ (∞) = f− (−∞) = 1, given by (4.52), lead to
. Because v± (x) satisfies Figs. (4.44a), (4.44b) and (4.46), the Hierarchy theorem proved in Section 3 applies. The boundary conditions f+ (∞) = f− (−∞) = 1, given by (4.52), lead to 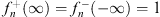 , in agreement with Figs. (4.55a) and (4.55b). According to Figs. (3.24), (3.25), (3.26) and (3.27) of Case (A) of the theorem, we have
, in agreement with Figs. (4.55a) and (4.55b). According to Figs. (3.24), (3.25), (3.26) and (3.27) of Case (A) of the theorem, we have
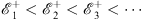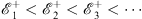
| (4.59a) |
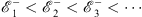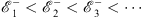
| (4.59b) |
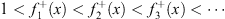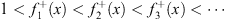
| (4.60a) |
at all finite and positive x, and
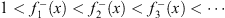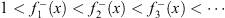
| (4.60b) |
at all finite and negative x. Since
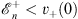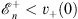
| (4.61a) |
and
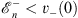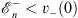
| (4.61b) |
with both v± (0) finite,
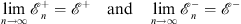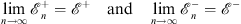
| (4.62) |
both exist. Furthermore, by using the integral equations Figs. (4.55a) and (4.55b) for 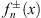 and by following the arguments similar to those given in Section 5 of [3], we can show that
and by following the arguments similar to those given in Section 5 of [3], we can show that
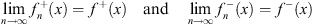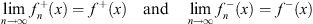
| (4.63) |
also exist. This leads us from the first trial function  (x) given by (4.3) to
(x) given by (4.3) to  f+ (x) and
f+ (x) and  f− (x) which are solutions of
f− (x) which are solutions of
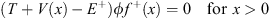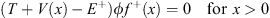
| (4.64a) |
and
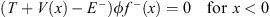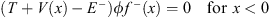
| (4.64b) |
with
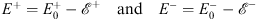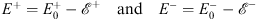
| (4.65) |
and the boundary conditions at x = 0,
 ′(0)=f+′(0)=f-′(0)=0. ′(0)=f+′(0)=f-′(0)=0.
| (4.66) |
An additional normalization factor multiplying, say, f− (x) would enable us to construct the second trial function χ (x) that satisfies Figs. (4.9), (4.10), (4.11), (4.12) and (4.13).
| <== previous lecture | | | next lecture ==> |
| Construction of the first trial function | | | Symmetric vs asymmetric potential |