
Construction of the first trial function
Date: 2015-10-07; view: 641.
We consider first the positive x region. Following Section 2.1, we begin with the usual perturbative power series expansion for
| ψ(x)=e-gS(x) | (4.18) |
with
gS(x)=gS0(+)+S1(+)+g-1S2(+)+ 
| (4.19) |
and
E=gE0(+)+E1(+)+g-1E2(+)+ 
| (4.20) |
in which Sn (+) and En (+) are g-independent. Substituting Figs. (4.18), (4.19) and (4.20) into the Schroedinger equation (4.2) and equating both sides, we find
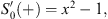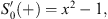
| (4.21) |
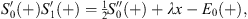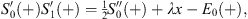
| (4.22) |
etc. Thus, (4.21) leads to
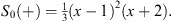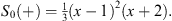
| (4.23) |
Since the left side of (4.22) vanishes at x = 1, so is the right side; hence, we determine
| E0(+)=1+λ, | (4.24) |
which leads to
| S1(+)=(1+λ)ln(1+x). | (4.25) |
Of course, the power series expansion Figs. (4.19) and (4.20) are both divergent. However, if we retain the first two terms in (4.19), the function
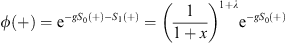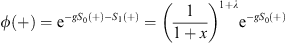
| (4.26) |
serves as a reasonable approximation of ψ (x) for x > 0, except when x is near zero. By differentiating  (+), we find
(+), we find  (+) satisfies
(+) satisfies
(T+V(x)+u+(x))  (+)=gE0(+) (+)=gE0(+)  (+) (+)
| (4.27) |
where

| (4.28) |
In order to construct the trial function  (x) that satisfies the boundary condition (4.5), we introduce for x
(x) that satisfies the boundary condition (4.5), we introduce for x  0,
0,
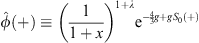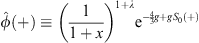
| (4.29) |
and
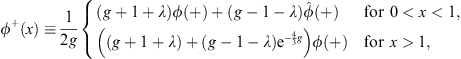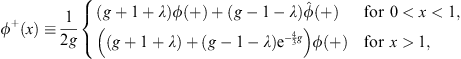
| (4.30) |
so that  + (x) and its derivative
+ (x) and its derivative  +′ (x) are both continuous at x = 1, and in addition, at x = 0 we have
+′ (x) are both continuous at x = 1, and in addition, at x = 0 we have  +′ (0) = 0. For x
+′ (0) = 0. For x  0, we observe that V (x) is invariant under
0, we observe that V (x) is invariant under
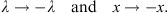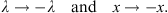
| (4.31) |
The same transformation converts  + (x) for x positive to
+ (x) for x positive to  − (x) for x negative. Define
− (x) for x negative. Define
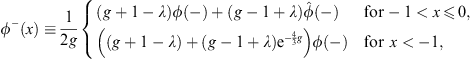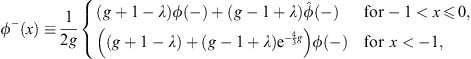
| (4.32) |
where
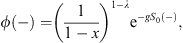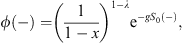
| (4.33) |
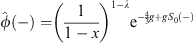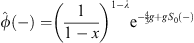
| (4.34) |
and
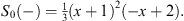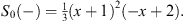
| (4.35) |
Both  − (x) and its derivative
− (x) and its derivative  −′ (x) are continuous at x = −1; furthermore,
−′ (x) are continuous at x = −1; furthermore,  + (x) and
+ (x) and  − (x) also satisfy the continuity condition Figs. (4.4) and (4.5), as well as the Schroedinger equation Figs. (4.6a) and (4.6b), with the perturbative potentials v+ (x) and v- (x) given by
− (x) also satisfy the continuity condition Figs. (4.4) and (4.5), as well as the Schroedinger equation Figs. (4.6a) and (4.6b), with the perturbative potentials v+ (x) and v- (x) given by

| (4.36a) |
and
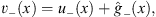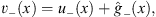
| (4.36b) |
in which u+ (x) is given by (4.28),
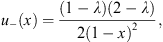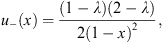
| (4.37) |
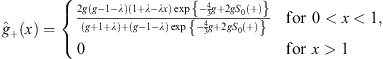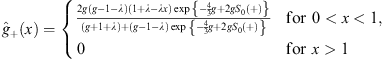
| (4.38a) |
and
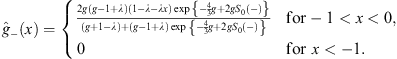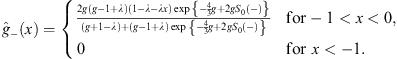
| (4.38b) |
In order that u+ (x), 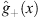 be positive for x > 0 and u- (x),
be positive for x > 0 and u- (x), 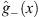 positive for x < 0, we impose
positive for x < 0, we impose
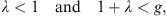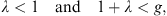
| (4.39) |
in addition to the earlier condition λ > 0. From Figs. (4.28) and (4.37), we have
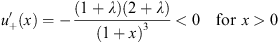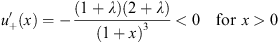
| (4.40a) |
and
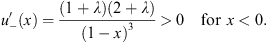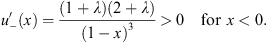
| (4.40b) |
Likewise, from Figs. (4.38a) and (4.38b), we find
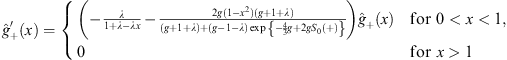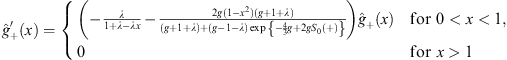
| (4.41a) |
and

| (4.41b) |
Furthermore, as x → ±1,
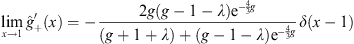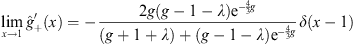
| (4.42a) |
and
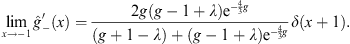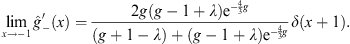
| (4.42b) |
Thus, for x  0, we have
0, we have
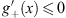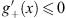
| (4.43) |
and, together with Figs. (4.36a) and (4.40a),
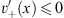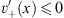
| (4.44a) |
for x positive. On the other hand for x  0,
0, 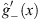 is not always positive; e.g., at x = 0,
is not always positive; e.g., at x = 0,
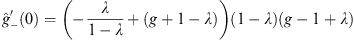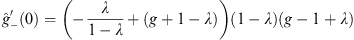
|
which is positive for 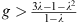 , but at x = −1+,
, but at x = −1+,
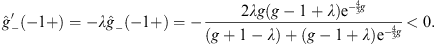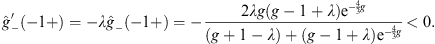
|
However, at x = −1, 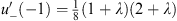 . It is easy to see that the sum
. It is easy to see that the sum 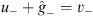 can satisfy for x
can satisfy for x  0,
0,
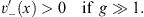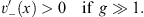
| (4.44b) |
To summarize:  + (x) and
+ (x) and  − (x) satisfy the Schroedinger equation Figs. (4.6a) and (4.6b), with v± (x) given by Figs. (4.36a) and (4.36b),
− (x) satisfy the Schroedinger equation Figs. (4.6a) and (4.6b), with v± (x) given by Figs. (4.36a) and (4.36b),
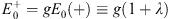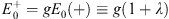
| (4.45a) |
and
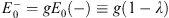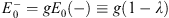
| (4.45b) |
and the boundary conditions Figs. (4.4) and (4.5). In addition, v± (x) satisfies
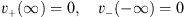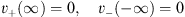
| (4.46) |
and the monotonicity conditions Figs. (4.7a) and (4.7b).
| <== previous lecture | | | next lecture ==> |
| Asymmetric quartic double-well problem | | | Construction of the second trial function |