
Asymmetric quartic double-well problem
Date: 2015-10-07; view: 780.
The hierarchy theorem established in the previous section has two restrictions: (i) the limitation of half-space x  0 and (ii) the requirement of a monotonically decreasing perturbative potential w (x). In this section, we shall remove these two restrictions.
0 and (ii) the requirement of a monotonically decreasing perturbative potential w (x). In this section, we shall remove these two restrictions.
Consider the specific example of an asymmetric quadratic double-well potential
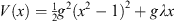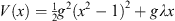
| (4.1) |
with the constant λ > 0. The ground state wave function ψ (x) and energy E satisfy the Schroedinger equation
| (T+V(x))ψ(x)=Eψ(x), | (4.2) |
where 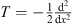 , as before. In the following, we shall present our method in two steps: We first construct a trial function
, as before. In the following, we shall present our method in two steps: We first construct a trial function  (x) of the form
(x) of the form
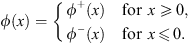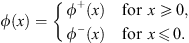
| (4.3) |
At x = 0,  (x) and
(x) and  ′ (x) are both continuous, given by
′ (x) are both continuous, given by
 (0)= (0)=  +(0)= +(0)=  -(0) -(0)
| (4.4) |
and
 ′(0)= ′(0)=  +′(0)= +′(0)=  -′(0)=0, -′(0)=0,
| (4.5) |
with prime denoting 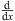 , as before. As we shall see, for x > 0, the trial function
, as before. As we shall see, for x > 0, the trial function  (x) =
(x) =  + (x) satisfies
+ (x) satisfies
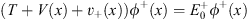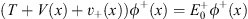
| (4.6a) |
with
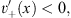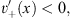
| (4.7a) |
whereas for x < 0,  (x) =
(x) =  − (x) satisfies
− (x) satisfies
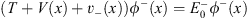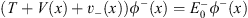
| (4.6b) |
with
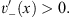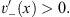
| (4.7b) |
Furthermore, at x = ±∞
| v+(∞)=v-(-∞)=0. | (4.8) |
Starting separately from  + (x) and
+ (x) and  − (x) and applying the hierarchy theorem, as we shall show, we can construct from
− (x) and applying the hierarchy theorem, as we shall show, we can construct from  (x) another trial function
(x) another trial function
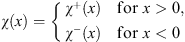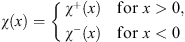
| (4.9) |
with χ (x) and χ′ (x) both continuous at x = 0, given by
| χ(0)=χ+(0)=χ-(0) | (4.10) |
and
| χ′(0)=χ+′(0)=χ-′(0)=0. | (4.11) |
In addition, they satisfy the following Schroedinger equations
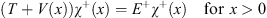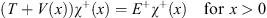
| (4.12) |
and
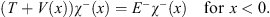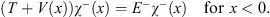
| (4.13) |
From V (x) given by (4.1) with λ positive, we see that at any x > 0, V (x) > V (−x); therefore, E+ > E−.
Our second step is to regard χ (x) as a new trial function, which satisfies
| (T+V(x)+w(x))χ(x)=E0χ(x) | (4.14) |
with w (x) being a step function,
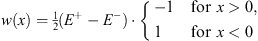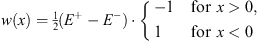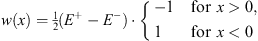
| (4.15) |
and
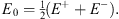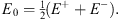
| (4.16) |
We see that w (x) is now monotonic, with
w′(x)  0 0
| (4.17) |
for the entire range of x from −∞ to +∞. The hierarchy theorem can be applied again, and that will lead from χ (x) to ψ (x), as we shall see.
| <== previous lecture | | | next lecture ==> |
| Hierarchy theorem and its generalization | | | Construction of the first trial function |