
Hierarchy theorem and its generalization
Date: 2015-10-07; view: 707.
In this section, we restrict our discussions to a one-dimensional problem, in which the potential V (x) is an even function of x, as in the example given in Section 2.2. The Schroedinger equation (1.9) becomes
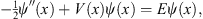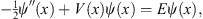
| (3.1) |
with ψ (x) as its ground state wave function, E the ground state energy, and ′ denoting 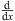 , as before. For the one-dimensional problem, the trial function
, as before. For the one-dimensional problem, the trial function  (x) satisfies
(x) satisfies
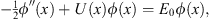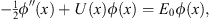
| (3.2) |
as in (1.11); therefore (3.1) can be written as
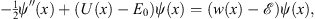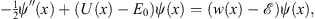
| (3.3) |
in which
| U(x)=V(x)+w(x) | (3.4) |
and
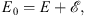
| (3.5) |
as before. Throughout this section, we assume
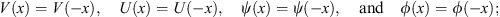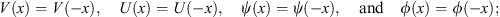
| (3.6) |
hence, we need only to consider
x  0. 0.
| (3.7) |
Furthermore, as in the example of the symmetric quartic double-well potential given in Section 2.2, we assume w (x) to satisfy
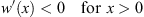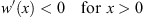
| (3.8) |
and
| w(∞)=0. | (3.9) |
Therefore, w (x) is positive for x positive. Otherwise, the shape of w (x) can be arbitrary. The Schroedinger equation (3.1) will be solved through the iterative steps Figs. (1.34), (1.35), (1.36), (1.37), (1.38), (1.39), (1.40), (1.41), (1.42) and (1.43), using the sequences
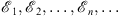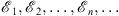
| (3.10) |
for the energy difference 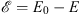 , and the sequence
, and the sequence
| f1(x),f2(x),…,fn(x),… | (3.11) |
for the ratio f (x) = ψ (x)/  (x) with, for n = 0,
(x) with, for n = 0,
| f0(x)=1. | (3.12) |
In this section, we differentiate two sets of sequences, labeled A and B, satisfying different boundary conditions:
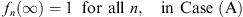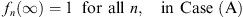
|
or
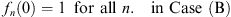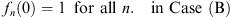
|
Thus, in accordance with Figs. (1.42) and (1.43), we have in Case (A)
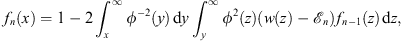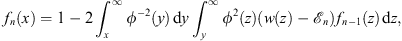
| (3.13A) |
whereas in Case (B)
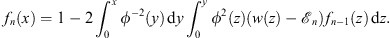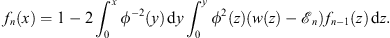
| (3.13B) |
In both cases, 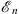 is determined by the corresponding fn − 1 (x) through Figs. (1.38) and (1.40); i.e.,
is determined by the corresponding fn − 1 (x) through Figs. (1.38) and (1.40); i.e.,
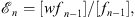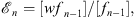
| (3.14) |
in which [F] of any function F (x) is defined to be
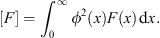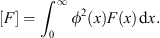
| (3.15) |
Eqs. Figs. (1.35) and (1.37) give
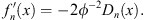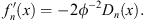
| (3.16) |
Likewise, Figs. (1.38) and (1.39) lead to
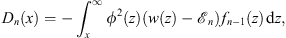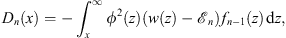
| (3.17) |
which, on account of (1.40), is identical to
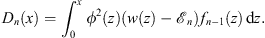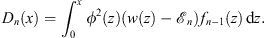
| (3.18) |
These two expressions of Dn (x) are valid for both Cases (A) and (B). Let xn be defined by
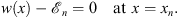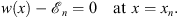
| (3.19) |
Since w′ (x) < 0, (3.19) has one and only one solution, with 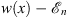 negative for x > xn and positive for x < xn. Thus, if
negative for x > xn and positive for x < xn. Thus, if
| fn-1(x)>0 | (3.20) |
for all x > 0, we have from Figs. (3.17) and (3.18)
| Dn(x)>0 | (3.21) |
and therefore, on account of (3.16),
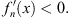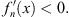
| (3.22) |
In terms of the electrostatic analog introduced in Section 1, through Figs. (1.26), (1.27), (1.28) and (1.29), one can form a simple physical picture of these expressions. Represent Dn (x) by the standard flux of lines of force. Because the dielectric constant κ (x) =  2 (x) is zero at x = ∞, so is the displacement field. Hence, Dn (∞) = 0; therefore each line of force must terminate at a finite point. Since the electric charge density is
2 (x) is zero at x = ∞, so is the displacement field. Hence, Dn (∞) = 0; therefore each line of force must terminate at a finite point. Since the electric charge density is 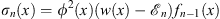 , the total electric charge to the right of x is
, the total electric charge to the right of x is
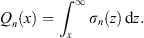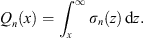
|
It must also be the negative of the flux Dn (x) passing through the same point x: i.e.,
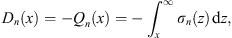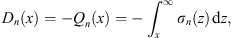
|
which gives (3.17). In the whole range from x = 0 to ∞, the total electric charge 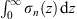 is zero; therefore, we have
is zero; therefore, we have
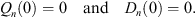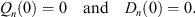
|
Furthermore, at any point x > 0, the total charge from the origin to the point x is
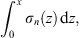
|
which must also be the negative of the above Qn (x), and therefore the same as Dn (x); that leads to (3.18). From (3.19) and w′ (x) < 0, one sees that the charge distribution σn (x) is negative for x > xn, 0 at x = xn, and positive for 0 < x < xn. Correspondingly, moving from x = ∞ towards the left, the displacement field increases from Dn (∞) = 0 to Dn (x) > 0, reaching its maximum at x = xn, then as x further decreases, so does Dn (x), and finally reaches Dn (0) = 0 at x = 0. In Case (A), because of fn (∞) = 1, (3.22) leads to
| fn(0)>fn(x)>fn(∞)=1. | (3.23A) |
Since for n = 0, f0 (x) = 1, Figs. (3.20) and (3.23A) are valid for n = 1; by induction these expressions also hold for all n; in Case (A), their validity imposes no restriction on the magnitude of w (x). In Case (B) we assume w (x) to be not too large, so that (3.13B) is consistent with
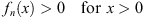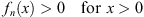
|
and therefore
| fn(0)=1>fn(x)>fn(∞)>0. | (3.23B) |
As we shall see, these two boundary conditions (A) and (B) produce sequences that have very different behavior. Yet, they also share a number of common properties.
Hierarchy Theorem (A) With the boundary condition fn (∞) = 1, we have for all n
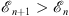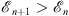
| (3.24) |
and
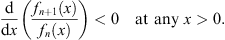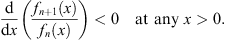
| (3.25) |
Thus, the sequences 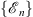 and {fn (x)} are all monotonic, with
and {fn (x)} are all monotonic, with
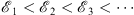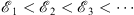
| (3.26) |
and
1<f1(x)<f2(x)<f3(x)< 
| (3.27) |
at all finite and positive x.
(B) With the boundary condition fn (0) = 1, we have for all odd n = 2m + 1 an ascending sequence
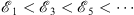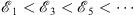
| (3.28) |
but for all even n = 2m, a descending sequence
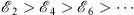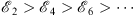
| (3.29) |
furthermore, between any even n = 2m and any odd n = 2l + 1
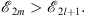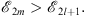
| (3.30) |
Likewise, at any x > 0, for any even n = 2m
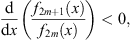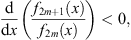
| (3.31) |
whereas for any odd n = 2l + 1
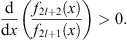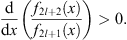
| (3.32) |
Remarks:
1. The validity of Eqs. Figs. (3.24) and (3.25) for the boundary condition fn (∞) = 1 was established in [4]. The validity of Eqs. Figs. (3.28), (3.29), (3.30), (3.31) and (3.32) for the boundary condition fn (0) = 1 is the new result of this paper, which we shall establish.
2. As we shall also show, the lowest eigenvalue E of the Hamiltonian T + V is the limit of the sequence {En} with
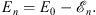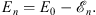
| (3.33) |
Thus, the boundary condition fn (∞) = 1 yields a sequence, in accordance with (3.26),
E1>E2>E3>  >E, >E,
| (3.34) |
with each member En an upper bound of E, similar to the usual variational iterative sequence.
3. On the other hand, with the boundary condition fn (0) = 1, while the sequence of its odd members n = 2l + 1 yields a similar one, like (3.34), with
E1>E3>E5>  >E, >E,
| (3.35) |
its even members n = 2m satisfy
E2<E4<E6<  <E. <E.
| (3.36) |
It is unusual to have an iterative sequence of lower bounds of the eigenvalue E. Together, these sequences may be quite efficient to pinpoint the limiting E.
The proof of the above generalized hierarchy theorem depends on several lemmas that are applicable to both boundary conditions: (A) fn (∞) = 1 and (B) fn (0) = 1; these lemmas will be established first, and then followed by the proof of the theorem.
Lemma 1
For any pair fm (x) and fl (x)
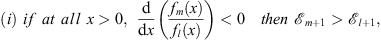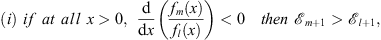
| (3.37) |
and
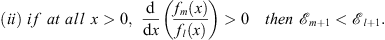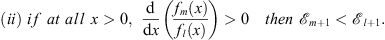
| (3.38) |
Proof
According to (3.14)
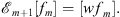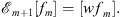
| (3.39) |
Also by definition (3.15),
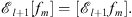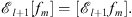
| (3.40) |
Their difference gives
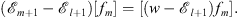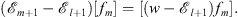
| (3.41) |
From (3.14),
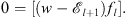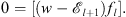
| (3.42) |
Let xl+1 be defined by (3.19). Multiplying (3.41) by fl (xl+1) and (3.42) by fm (xl+1) and taking their difference, we have
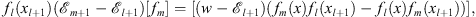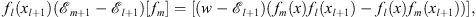
| (3.43) |
in which the unsubscripted x acts as a dummy variable; thus [fm (x)] means [fm] and [fm (xl+1)] means fm (xl+1) · [1], etc.
(i) If (fm (x)/fl (x))′ < 0, then for x < xl + 1
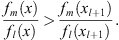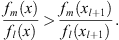
| (3.44) |
In addition, since w′ (x) < 0 and 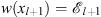 , we also have for x < xl+1
, we also have for x < xl+1
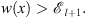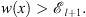
| (3.45) |
Thus, the function inside the square bracket on the right-hand side of (3.43) is positive for x < xl+1. Also, the inequalities Figs. (3.44) and (3.45) both reverse their signs for x > xl+1. Consequently, the right-hand side of (3.43) is positive definite, and so is its left side. Therefore, on account of Figs. (3.23A) and (3.23B), (3.37) holds.
(ii) If (fm (x)/fl (x))′ > 0, we see that for x < xl+1, (3.44) reverses its sign but not (3.45). A similar reversal of sign happens for x > xl+1. Thus, the right-hand side of (3.43) is now negative definite and therefore 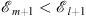 . Lemma 1 is proved.
. Lemma 1 is proved. 
The following lemma was already proved in [4]. For the convenience of the readers, we also include it in this paper. Let
| η=η(ξ) | (3.46) |
be a single-valued differentiable function of ξ in the range between a and b with
0  a a  ξ ξ  b b
| (3.47) |
and with
η(a)  0. 0.
| (3.48) |
Lemma 2
(i) The ratio η/ξ is a decreasing function of ξ for a < ξ < b if
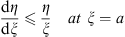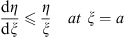
| (3.49) |
and
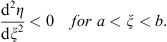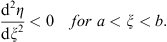
| (3.50) |
(ii) The ratio η/ξ is an increasing function of ξ for a < ξ < b if
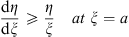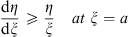
| (3.51) |
and
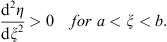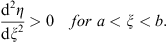
| (3.52) |
Proof
Define
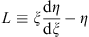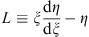
| (3.53) |
to be the Legendre transform L (ξ). We have
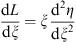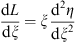
| (3.54) |
and
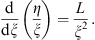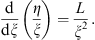
| (3.55) |
Since (3.49) says that L (a)  0 and (3.50) says that
0 and (3.50) says that 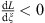 for a < ξ < b, these two conditions imply L (ξ) < 0 for a < ξ < b, which proves (i) in view of (3.55). The proof of (ii) is the same, but with inequalities reversed.
for a < ξ < b, these two conditions imply L (ξ) < 0 for a < ξ < b, which proves (i) in view of (3.55). The proof of (ii) is the same, but with inequalities reversed. 
Lemma 3
For any pair fm (x) and fl (x)
(i) if over all x > 0,
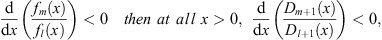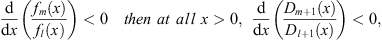
| (3.56) |
and (ii) if over all x > 0,
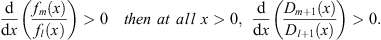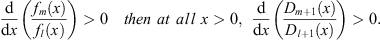
| (3.57) |
Proof
From Figs. (3.17) and (3.18), we have
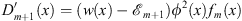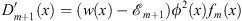
| (3.58) |
and
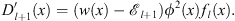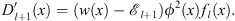
| (3.59) |
Define
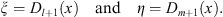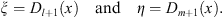
| (3.60) |
In any local region of x where 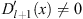 , we can regard η = η (ξ) through η (x) = η (ξ (x)). Hence, we have
, we can regard η = η (ξ) through η (x) = η (ξ (x)). Hence, we have
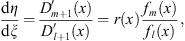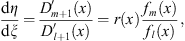
| (3.61) |
where
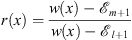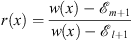
| (3.62) |
and
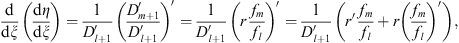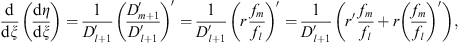
| (3.63) |
where
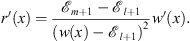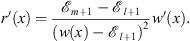
| (3.64) |
(i) If (fm/fl)′ < 0, from Lemma 1, we have
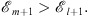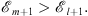
| (3.65) |
From w′ (x) < 0 and the definition of xm + 1 and xl + 1, given by (3.19), we have
| xm+1<xl+1, | (3.66) |
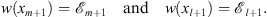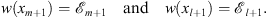
| (3.67) |
We note that from Figs. (3.17) and (3.18) Dm + 1 (x) and Dl + 1 (x) are both positive continuous functions of x, varying from at x = 0,
| Dm+1(0)=Dl+1(0)=0 | (3.68) |
to at x = ∞
| Dm+1(∞)=Dl+1(∞)=0 | (3.69) |
with their maxima at xm + 1 for Dm + 1 (x) and xl + 1 for Dl + 1 (x), since in accordance with Figs. (3.58), (3.59) and (3.67),
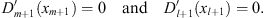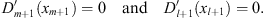
| (3.70) |
From Figs. (3.64) and (3.65), we see that r′ (x) is always <0. Furthermore, from (3.62), we also find that the function r (x) has a discontinuity at x = xl + 1. At x = 0, r (0) satisfies
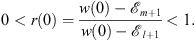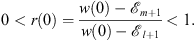
| (3.71) |
As x increases from 0, r (x) decreases from r (0), through
| r(xm+1)=0, | (3.72) |
to −∞ at x = xl + 1−; r (x) then switches to +∞ at x = xl + 1+, and continues to decrease as x increases from xl + 1+. At x = ∞, r (x) becomes
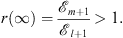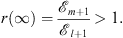
| (3.73) |
It is convenient to divide the positive x-axis into three regions:
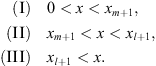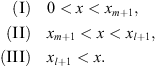
| (3.74) |
Table 1 summarizes the signs of 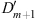 ,
, 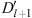 , r, and r′ in these regions. Assuming (fm/fl)′ < 0 we shall show separately the validity of (3.56), (Dm + 1/Dl + 1)′ < 0, in each of these three regions.
, r, and r′ in these regions. Assuming (fm/fl)′ < 0 we shall show separately the validity of (3.56), (Dm + 1/Dl + 1)′ < 0, in each of these three regions.
 Table 1.
Table 1.
The signs of 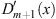 ,
, 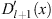 ,
, 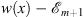 ,
, 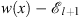 , r (x), and r′ (x) in the three regions defined by (3.74), when
, r (x), and r′ (x) in the three regions defined by (3.74), when 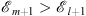
| Region | 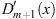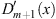
| 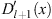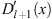
| 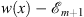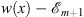
| 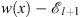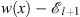
| r (x) | r′ (x) |
| I | >0 | >0 | >0 | >0 | >0 | < 0 |
| II | <0 | >0 | <0 | >0 | <0 | <0 |
| III | <0 | <0 | <0 | <0 | >0 | <0 |

Since
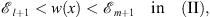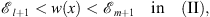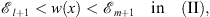
| (3.75) |
Dm + 1 (x) is decreasing and Dl + 1 (x) is increasing; it is clear that (3.56) holds in (II).
In each of regions (I) and (III), we have r (x) > 0 from (3.62) and r′ (x) < 0 from (3.64). Since (fm/fl)′ is always negative by the assumption in (3.56), both terms inside the big parentheses of (3.63) are negative; hence the same (3.63) states that d2η/dξ2 has the opposite sign from 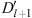 . From the sign of
. From the sign of 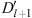 listed in Table 1, we see that
listed in Table 1, we see that
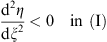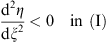
| (3.76) |
and
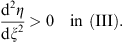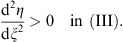
| (3.77) |
Within each region, η = Dm + 1 (x) and ξ = Dl + 1 (x) are both monotonic in x; therefore, η is a single-valued function of ξ and we can apply Lemma 2. In (I), at x = 0, both Dm + 1 (0) and Dl + 1 (0) are 0 according to (3.18), but their ratio is given by
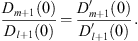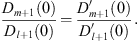
| (3.78) |
Therefore,
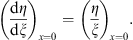
| (3.79) |
Furthermore, from (3.76), 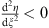 in (I), it follows from Lemma 2, Case (i), the ratio η/ξ is a decreasing function of ξ. Since
in (I), it follows from Lemma 2, Case (i), the ratio η/ξ is a decreasing function of ξ. Since 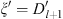 is >0 in (I), according to (3.59), we have
is >0 in (I), according to (3.59), we have
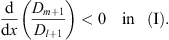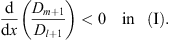
| (3.80) |
In (III), at x = ∞, both Dm + 1 (∞) and Dl + 1 (∞) are 0 according to (3.69). Their ratio is
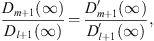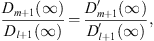
|
which gives at x = ∞,
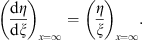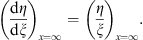
| (3.81) |
As x decreases from x = ∞ to x = xl + 1, from (3.77) we have 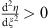 in (III). It follows from Lemma 2, Case (ii), η/ξ is an increasing function of ξ. Since
in (III). It follows from Lemma 2, Case (ii), η/ξ is an increasing function of ξ. Since 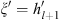 is <0, because x > xl + 1, we have
is <0, because x > xl + 1, we have
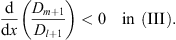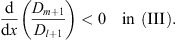
| (3.82) |
Thus, we prove Case (i) of Lemma 3. Case (ii) of Lemma 3 follows from Case (i) through the interchange of the subscripts m and l. Lemma 3 is then established. 
Lemma 4
Take any pair fm (x) and fl (x)(A) For the boundary condition fn (∞) = 1, if at all x > 0,
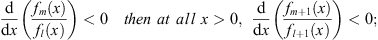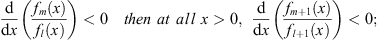
| (3.83A) |
therefore, if at all x > 0,
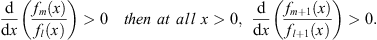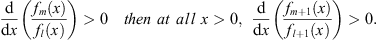
| (3.84A) |
(B) For the boundary condition fn (0) = 1, if at all x > 0,
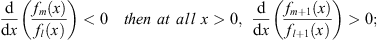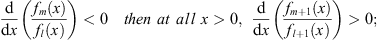
| (3.83B) |
therefore, if at all x > 0,
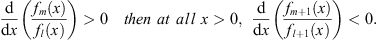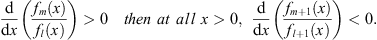
| (3.84B) |
Proof
Define
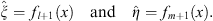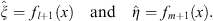
| (3.85) |
From (1.35) we see that
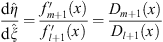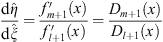
| (3.86) |
and
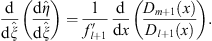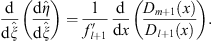
| (3.87) |
(A) In this case fn (∞) = 1 for all n. Thus, at x = ∞, 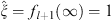 ,
, 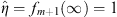 , and their ratio
, and their ratio
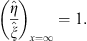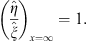
| (3.88) |
At the same point x = ∞, in accordance with (3.17), Dl + 1 (∞) = Dm + 1 (∞) = 0, but their ratio is, on account of w (∞) = 0 and (3.37) of Lemma 1,
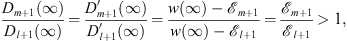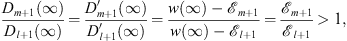
| (3.89) |
in which the last inequality follows from the same assumption, if (fm/fl)′ < 0, shared by (3.37) of Lemma 1 and the present (3.83A) that we wish to prove. Thus, from (3.86), at x = ∞
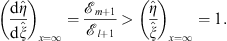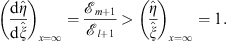
| (3.90) |
As x decreases from ∞ to 0, 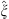 increases from fl + 1 (∞) = 1 to fl + 1 (0) > 1, in accordance with Figs. (3.22) and (3.23A). On account of (3.56) of Lemma 3, we have (Dm + 1/Dl + 1)′ < 0, which when combined with (3.87) and
increases from fl + 1 (∞) = 1 to fl + 1 (0) > 1, in accordance with Figs. (3.22) and (3.23A). On account of (3.56) of Lemma 3, we have (Dm + 1/Dl + 1)′ < 0, which when combined with (3.87) and 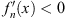 leads to
leads to
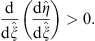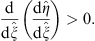
| (3.91) |
Thus, by using Figs. (3.51) and (3.52) of Lemma 2, we have 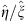 to be an increasing function of
to be an increasing function of 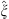 ; i.e.,
; i.e.,
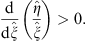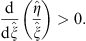
| (3.92) |
Because
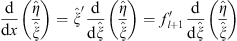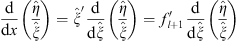
| (3.93) |
and 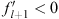 , we find
, we find
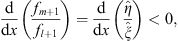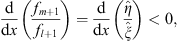
| (3.94) |
which establishes (3.83A). Through the interchange of the subscripts m and l, we also obtain (3.84A).
Next, we turn to Case (B) with the boundary condition fn (0) = 1 for all n. Therefore at x = 0,
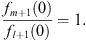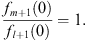
| (3.95) |
Furthermore from Figs. (3.16) and (3.18), we also have 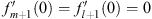 and Dm + 1 (0) = Dl + 1 (0) = 0, with their ratio given by
and Dm + 1 (0) = Dl + 1 (0) = 0, with their ratio given by
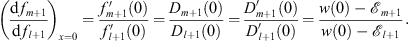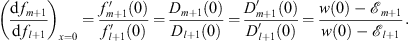
| (3.96) |
From (3.37) of Lemma 1, we see that if (fm/fl)′ < 0, then 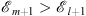 and therefore
and therefore
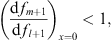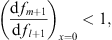
| (3.97) |
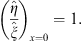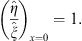
| (3.98) |
Thus,
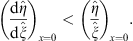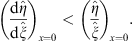
| (3.99) |
Analogously to (3.53), define
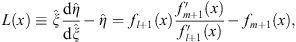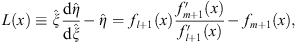
| (3.100) |
therefore
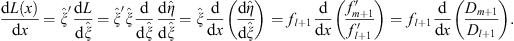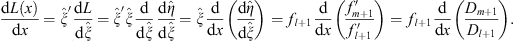
| (3.101) |
From (3.56) of Lemma 3, we know that if (fm/fl)′ < 0 then (Dm + 1/Dl + 1)′ < 0, which leads to
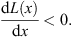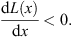
| (3.102) |
From (3.100), we have
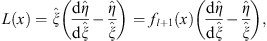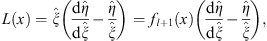
| (3.103) |
and therefore at x = 0, because of (3.99),
| L(0)<0. | (3.104) |
Combining Figs. (3.102) and (3.104), we derive
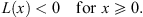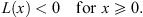
| (3.105) |
Multiplying (3.100) by 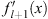 , we have
, we have
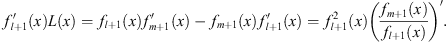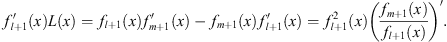
| (3.106) |
Because 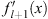 and L (x) are both negative, it follows then
and L (x) are both negative, it follows then
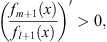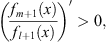
|
which gives (3.83B) for Case (B), with the boundary condition fn (0) = 1. Interchanging the subscripts m and l, (3.83B) becomes (3.84B), and Lemma 4 is established. 
We now turn to the proof of the theorem stated in Figs. (3.24), (3.25), (3.26), (3.27), (3.28), (3.29), (3.30), (3.31) and (3.32).
Proof of the hierarchy theorem. When n = 0, we have
| f0(x)=1. | (3.107) |
From Figs. (3.20), (3.21) and (3.22), we find for n = 1
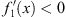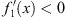
| (3.108) |
and therefore
| (f1/f0)′<0. | (3.109) |
In Case (A), by using (3.83A) and by setting m = 1 and l = 0, we derive (f2/f1)′ < 0; through induction, it follows then (fn + 1/fn)′ < 0 for all n. From Lemma 1, we also find 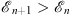 for all n. Thus, Figs. (3.24), (3.25), (3.26) and (3.27) are established.
for all n. Thus, Figs. (3.24), (3.25), (3.26) and (3.27) are established.
In Case (B), by using Figs. (3.109) and (3.83B), and setting m = 1 and l = 0, we find (f2/f1)′ > 0, which in turn leads to (f3/f2)′ < 0, … , and Figs. (3.31) and (3.32). Inequalities Figs. (3.28), (3.29) and (3.30) now follow from Figs. (3.37) and (3.38) of Lemma 1. The Hierarchy Theorem is proved.
Assuming that w (0) is finite, we have for any n
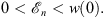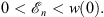
| (3.110) |
Therefore, each of the monotonic sequences
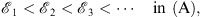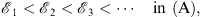
|
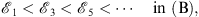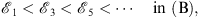
|
and
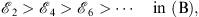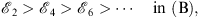
|
converges to a finite limit 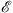 . By following the discussions in Section 5 of [4], one can show that each of the corresponding monotonic sequences of fn (x) also converges to a finite limit f (x). The interchange of the limit n → ∞ and the integrations in (3.13A) completes the proof that in Case (A) the limits
. By following the discussions in Section 5 of [4], one can show that each of the corresponding monotonic sequences of fn (x) also converges to a finite limit f (x). The interchange of the limit n → ∞ and the integrations in (3.13A) completes the proof that in Case (A) the limits 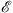 and f (x) satisfy
and f (x) satisfy
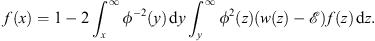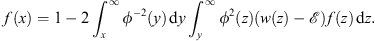
| (3.111A) |
As noted before, the convergence in Case (A) can hold for any large but finite w (x), provided that w′ (x) is negative for x > 0. In Case (B), a large w (x) may yield a negative fn (x), in violation of (3.23B) . Therefore, the convergence does depend on the smallness of w (x). One has to follow discussions similar to those given in [3] to ensure that the limits 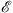 and f (x) satisfy
and f (x) satisfy
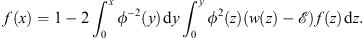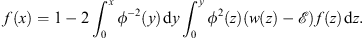
| (3.111B) |
| <== previous lecture | | | next lecture ==> |
| Trial function for the quantum double-well potential | | | Asymmetric quartic double-well problem |