
Appendix A. A soluble example
Date: 2015-10-07; view: 825.
In this appendix, we consider a soluble model in which the potential V (x) of (4.67) is

| (A.1) |
with W2 > μ2 and
| γ=α+β. | (A.2) |
Following (4.68), we introduce two symmetric potentials:

| (A.3) |
with, for x  0,
0,

| (A.4) |
and

| (A.5) |
so that (A.1) can also be written as

| (A.6) |
Let ψ (x), χa (x), and χb (x) be, respectively, the ground state wave functions of
| (T+V(x))ψ(x)=Eψ(x), | (A.7) |
| (T+Va(x))χa(x)=Eaχa(x) | (A.8) |
and
| (T+Vb(x))χb(x)=Ebχb(x). | (A.9) |
For |x| > γ, since V (x) = ∞, we have
| ψ(x)=χa(x)=χb(x)=0. |
For |x| < γ, these wave functions are of the form

| (A.10) |

| (A.11) |
and

| (A.12) |
By substituting these solutions to the Schroedinger equations Figs. (A.7), (A.8) and (A.9), we derive

| (A.13) |

| (A.14) |
and

| (A.15) |
The continuity of ψ′/ψ at x = ±α relates
| -kβcotkβ=qβtanhq(α-δ) | (A.16) |
and
| -pβcotpβ=qβtanhq(α+δ) | (A.17) |
with β given by (A.2). In the following, we assume the barrier heights W and

| (A.18) |
to be much larger than k and p; therefore, the wave function ψ is mostly contained within the two square wells; i.e., kβ and pβ are both near π. We write

| (A.19) |
and expect  and θ to be small. Likewise, introduce
and θ to be small. Likewise, introduce

| (A.20) |
The explicit forms of these angles can be most conveniently derived by recognizing the separate actions of two related small parameters: one proportional to the inverse of the barrier height
(Wβ)-1  1 1
| (A.21) |
and the other
| e-2Wα<<<1, | (A.22) |
denoting the much smaller tunneling coefficient.
To illustrate how these two effects can be separated, let us consider first the determination of θb given by (A.20). The continuity of  at x = ±α gives
at x = ±α gives
| -pbβcotpbβ=qbβtanhqbα. | (A.23) |
From (A.15), we also have

| (A.24) |
Although the two small parameters Figs. (A.21) and (A.22) are not independent, their effects can be separated by introducing p∞ and q∞ that satisfy
| -p∞βcotp∞β=q∞β | (A.25) |
and

| (A.26) |
Physically, p∞ and q∞ are the limiting values of pb and qb when the distance 2α between the two wells → ∞, but keeping the shapes of the two wells unchanged. Hence Figs. (A.23) and (A.25). Let
| p∞β=π-θ∞. | (A.27) |
From (A.25), we may expand θ∞ in terms of successive powers of (Wβ)−1:

| (A.28) |
which determines both p∞ and q∞. By substituting
| θb=θ∞+ν1e-2q∞α+O(e-4q∞α) | (A.29) |
into (A.23) and using Figs. (A.24), (A.25), (A.26), (A.27) and (A.28), we determine

| (A.30) |
Likewise, the continuity of  at x = ±α gives
at x = ±α gives
| -kaβcotkaβ=qaβtanhkaα, | (A.31) |
with

| (A.32) |
As in (A.25), we introduce k∞ and  that satisfy
that satisfy
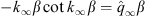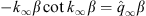
| (A.33) |
and

| (A.34) |
Similar to Figs. (A.27) and (A.28), we define

| (A.35) |
and derive
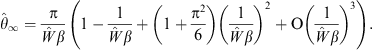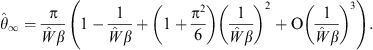
| (A.36) |
As in Figs. (A.29) and (A.30), we find  to be given by
to be given by

| (A.37) |
with

| (A.38) |
To derive similar expressions for θ and  of (A.19), we first note that the transformation
of (A.19), we first note that the transformation
| α→α+δ | (A.39) |
brings Figs. (A.23) and (A.17), provided that we also change

|
and therefore
| θb→θ. | (A.40) |
Since according to (A.1), the asymmetry of V (x) is due to the term  in the positive x region, it is easy to see that
in the positive x region, it is easy to see that
| δ>0, | (A.41) |
as will also be shown explicitly below. Thus, from (A.29) and through the transformations Figs. (A.39) and (A.40), we derive
| θ=θ∞+θ1, | (A.42) |
where
| θ1=ν1e-2q∞(α+δ)+O(e-4q∞(α+δ)) | (A.43) |
with ν1 given by (A.30). Likewise, we note that the transformation
| α→α-δ | (A.44) |
brings Figs. (A.31) and (A.16), provided that we also change

|
and therefore

| (A.45) |
Here, we must differentiate three different situations:

| (A.46) |
and

|
In Case (i), when
e-2q∞(α-δ)  1, 1,
| (A.47) |
from (A.37) and through the transformations given by Figs. (A.44) and (A.45), we find

| (A.48) |
where

| (A.49) |
with  given by (A.38). According to Figs. (A.13) and (A.19), we have
given by (A.38). According to Figs. (A.13) and (A.19), we have

| (A.50) |
which leads to

| (A.51) |
Since in accordance from Figs. (A.28) and (A.36), we find

| (A.52) |
and

| (A.53) |
Thus, the left side of (A.51) is dominated by its first term, μ2β2. Since θ1 and  are exponentially small, we can neglect
are exponentially small, we can neglect  in (A.51). In addition, because θ∞ and
in (A.51). In addition, because θ∞ and  are much smaller than 2π, (A.51) can be reduced to
are much smaller than 2π, (A.51) can be reduced to

| (A.54) |
which gives the dependence of δ on μ2. It is important to note that an exponentially small μ2 can produce a finite δ. For δ < α, at x = δ we have, in accordance with (A.10)
| ψ′(δ)=0, | (A.55) |
which gives the minimum of ψ (x). The wave function ψ (x) has two maxima, one for each potential well.
In Case (ii), α = δ and (A.16) gives cot kβ = 0, and  takes on the critical value
takes on the critical value  with
with

| (A.56) |
In Case (iii), 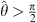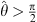 ,
,  and ψ (x) has only one maximum.
and ψ (x) has only one maximum.
As in Figs. (4.73) and (4.75) we introduce χ (x) through

| (A.57) |
so that

| (A.58) |
in which, same as Figs. (4.76a) and (4.77a),

| (A.59) |
and

| (A.60) |
with Ea and Eb given by Figs. (A.14) and (A.15). Since according to Figs. (A.4) and (A.5), Va (x)  Vb (x), we have
Vb (x), we have
| Ea>Eb; | (A.61) |
therefore,

| (A.62) |
Write the Schroedinger equation (A.7) in the form (4.80):

| (A.63) |
with

| (A.64) |
As in (4.82), we have

| (A.65) |
In all subsequent equations, we restrict the x-axis to
|x|  γ, γ,
| (A.66) |
and set ψ (x), χ (x) positive. Define
| f(x)=ψ(x)/χ(x). | (A.67) |
We have, as in Figs. (4.84) and (4.85),

| (A.68) |
or, on account of (A.65), the equivalent form

| (A.69) |
The derivation of f (x) is given by
| f′(x)=-2χ-2(x)h(x), | (A.70) |
where

| (A.71) |
or equivalently,

| (A.72) |
In order to satisfy (A.65) and by using (A.59), we see that

| (A.73) |
Thus, Figs. (A.71), (A.72) and (A.73) give

| (A.74) |
The positivity of h (x) gives

| (A.75) |
| <== previous lecture | | | next lecture ==> |
| References | | | A.1. A two-level model |