
A.1. A two-level model
Date: 2015-10-07; view: 666.
Before discussing the iterative solutions for f (x) and 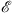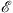 , it may be useful to first extract some essential features of the soluble square-well example. Let us first concentrate on Case (i) of (A.46), with the parameters α and δ satisfying
, it may be useful to first extract some essential features of the soluble square-well example. Let us first concentrate on Case (i) of (A.46), with the parameters α and δ satisfying
e-2q∞α  e-2q∞(α-δ) e-2q∞(α-δ)  1. 1.
| (A.76) |
We shall also neglect (Wα)−1 or (Wβ)−1, when compared to 1. Thus, from Figs. (A.27) and (A.28), we have
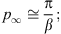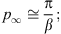
| (A.77) |
in addition, from Figs. (A.30) and (A.38) we find

| (A.78) |
From (A.54), we have

| (A.79) |
On account of Figs. (A.15), (A.20), (A.27) and (A.29),

| (A.80) |
which, for

| (A.81) |
gives

| (A.82) |
On the other hand, from Figs. (A.13), (A.19), (A.42) and (A.43), we see that

| (A.83) |
Thus, under the condition (A.76), we find

| (A.84) |
As we shall see, these inequalities can be understood in terms of a simple two-level model.
Introduce
| λ=E∞-Eb. | (A.85) |
We note that from (A.82),

| (A.86) |
and from Figs. (A.79) and (A.83),
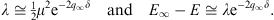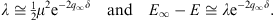
| (A.87) |
Consequently, the three small energy parameters in (A.84) are related by

| (A.88) |
From e-2q∞δ  1 and (A.76) , we see that
1 and (A.76) , we see that

| (A.89) |
in accordance with Figs. (A.79) and (A.84). To understand the role of the parameter λ, we may start with the definition of Vb (x), given by (A.5), keep the parameters β = γ − α and  fixed, but let the spacing 2α between the two potential wells approach ∞; in the limit 2α → ∞, we have Eb → E∞. Thus, λ = E∞ − Eb is the energy shift due to the tunneling between the two potential wells located at x < −α and x > α in Vb (x).
fixed, but let the spacing 2α between the two potential wells approach ∞; in the limit 2α → ∞, we have Eb → E∞. Thus, λ = E∞ − Eb is the energy shift due to the tunneling between the two potential wells located at x < −α and x > α in Vb (x).
There is an alternative definition for λ, which may further clarify its physical significance. According to (A.3), Vb (x) is even in x; therefore, its eigenstates are either even or odd in x. In (A.9), χb (x) is the ground state of T + Vb (x), and therefore it has to be even in x. The corresponding first excited state χod is odd in x; it satisfies
| (T+Vb(x))χod(x)=Eodχod(x). | (A.90) |
We may define λ by
| 2λ≡Eod-Eb | (A.91) |
and regard Figs. (A.85) and (A.86) both as approximate expressions, as we shall see.
Multiplying (A.9) by χod (x) and (A.90) by χb (x), then taking their difference we derive

| (A.92) |
From (A.12), we may choose the normalization of χb so that

| (A.93) |
Correspondingly,

| (A.94) |
with

| (A.95) |
As in Figs. (A.25) and (A.26), qod and pod are determined by
| -podβcotpodβ=qodβcothqodα | (A.96) |
and
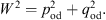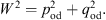
| (A.97) |
At x = 0, we have

| (A.98) |
Integrating (A.92) from x = 0 to x = γ, we find

| (A.99) |
From Figs. (A.27), (A.28) and (A.29), we see that

| (A.100) |
Likewise, we can also show that

| (A.101) |
Thus, qod  qb
qb  W, and the integral in (A.99) is
W, and the integral in (A.99) is

| (A.102) |
Since qod  W, we derive from (A.91)
W, we derive from (A.91)

| (A.103) |
in agreement with (A.86).
We are now ready to introduce the two-level model. We shall approximate the Hamiltonian T + V (x), T + Va (x), and T + Vb (x) of Figs. (A.7), (A.8) and (A.9) by the following three 2 × 2 matrices:

| (A.104) |

| (A.105) |
and

| (A.106) |
with ψ, χa, and χb as their respective ground states which satisfy
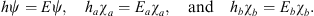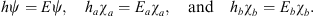
| (A.107) |
The negative sign in the off-diagonal matrix element −λ in Figs. (A.104), (A.105) and (A.106) is chosen to make

| (A.108) |
simulating the evenness of χa (x) and χb (x). Likewise, the analog of χod is the excited state of hb, with

| (A.109) |
and
| hbχod=Eodχod. | (A.110) |
It is straightforward to verify that

| (A.111) |
where

| (A.112) |

| (A.113) |
When  , we have
, we have

| (A.114) |
in agreement with (A.88).
Next, we wish to examine the relation between the two-level model and the soluble square-well example when λ is  . Assume, instead of (A.76),
. Assume, instead of (A.76),

| (A.115) |
Hence, in the square-well example, (A.83),

|
and (A.86),
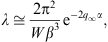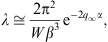
|
remain valid; on the other hand, Figs. (A.54) and (A.78) now lead to

| (A.116) |
Thus, the above expressions for E∞ − E and λ give
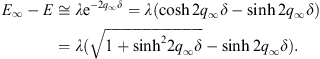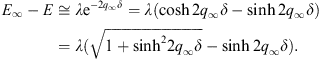
|
Together with (A.116), this shows that the soluble square-well example yields

|
in agreement with (A.113) given by the two-level model.
In both the square-well problem and the simple two-level model, we can also examine the limit, when  . In that case, (A.113) gives
. In that case, (A.113) gives

|
which leads to

|
in agreement with the exact square-well solution. Furthermore, if we include the first-order correction in O (μ2), (A.115) gives

| (A.117) |
As we shall discuss, for the exact square-well solution, (A.117) is also valid. Thus, the simple two-level formula (A.113) may serve as an approximate formula for the exact square-well solution over the entire range of  .
.
| <== previous lecture | | | next lecture ==> |
| Appendix A. A soluble example | | | A.2. Square-well example (Cont.) |