A.2. Square-well example (Cont.)

Date: 2015-10-07; view: 531.

We return to the soluble square-well example discussed in Appendix A.1. As before, ψ (x) is the ground state of T + V (x) with energy E, which is determined by the Schroedinger equation (A.7). Likewise, χ (x) is the trial function given by (A.57); i.e., the ground state of with eigenvalue Eˆ₀ = E_a, in accordance with Figs. (A.58), (A.59) and (A.60). From Figs. (A.59) and (A.65), we see that the energy difference

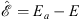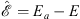
(A.118)

satisfies

(A.119)

where

(A.120)

and

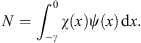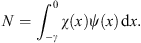
(A.121)

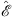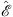Before we discuss the iterative sequence that approaches , as n → ∞, it may be instructive to verify (A.119) by evaluating the integrals Figs. (A.120) and (A.121) directly. Choose the normalization convention of ψ and χ so that at x = γ

(A.122)

From Figs. (A.10), (A.11) and (A.12) and (A.57) we write

(A.123)

(A.124)

By directly evaluating the integral ∫χ (x)ψ (x) dx, we can readily verify that for γ x 0

(A.125)

and for −γ x 0,

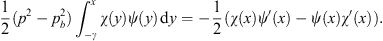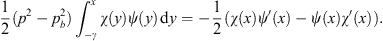
(A.126)

Both relations can also be inferred from the Schroedinger equations Figs. (A.7) and (A.58). Setting x = 0 and taking the sum (A.125) + (A.126), we derive

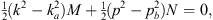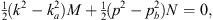
which, on account of Figs. (A.13), (A.14), (A.15), (A.16), (A.17) and (A.18), leads to the expression for the energy shift 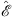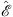, in agreement with (A.119).

Next, we proceed to verify directly that f (x) = ψ (x)/χ (x) satisfies the integral equation (A.68). With the normalization choice (A.122), we find at x = γ, since ψ (γ) = χ (γ) = 0,

(A.127)

which gives the constant in the integral equation. The same equation (A.68) can also be cast in an equivalent form:

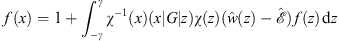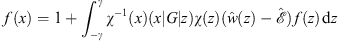
(A.128)

where (x|G|z) is the Green's function that satisfies

(A.129)

For x < z, (x|G|z) is given by

(A.130)

where

(A.131)

is the irregular solution of the same Schroedinger equation (A.58), satisfied by χ (x). That is,

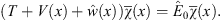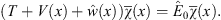
(A.132)

Consequently, over the entire range −γ < x < γ

(A.133)

According to Figs. (A.11), (A.12) and (A.57), we have

(A.134)

where A and B are constants given by

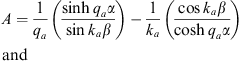
(A.135)

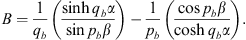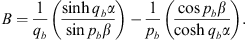
Since in (A.128), there are only single integrations of the products χ (z)ψ (z) and 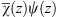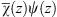, one can readily verify that f (x) satisfies the integral equation, and therefore also its equivalent form (A.68).