
A.3. The iterative sequence
Date: 2015-10-07; view: 685.
The integral equation (A.68), or its equivalent form (A.128), will now be solved iteratively by introducing
| ψn(x)=χ(x)fn(x). | (A.136) |
As in Figs. (4.87), (4.88) and (4.89), fn (x) and its associated energy 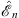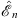 are determined by
are determined by
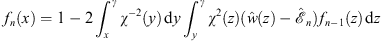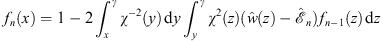
| (A.137) |
and
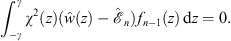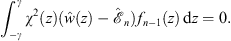
| (A.138) |
When n = 0, we set
| f0(x)=1. | (A.139) |
Introduce
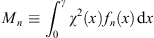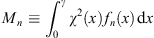
| (A.140) |
and
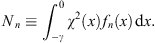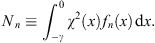
| (A.141) |
From (A.59) and

| (A.142) |
we derive
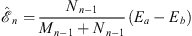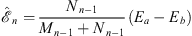
| (A.143) |
and
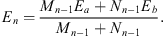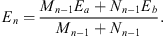
| (A.144) |
For n = 1, we have from Figs. (A.139), (A.140) and (A.141),
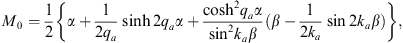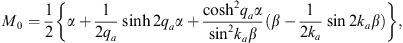
| (A.145) |
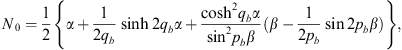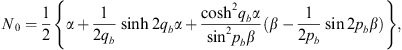
| (A.146) |
and

| (A.147) |
For small μ2, since Ea−Eb and M0−N0 are both O (μ2), we find

| (A.148) |
in agreement with (A.117), given by the simple two-level formula.
Next, we examine the integration for fn (x). Consider first the region
| α<x<γ, | (A.149) |
(A.137) can be written as
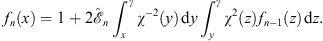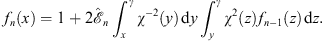
| (A.150) |
Introduce
| ξ=ka(-x+γ), | (A.151) |
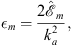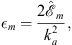
| (A.152) |
and
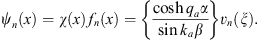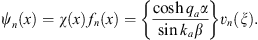
| (A.153) |
When n = 0, we set
| v0(ξ)=sinξ. | (A.154) |
From (A.150), or more conveniently by using (x|G|z) given by (A.130), one can readily verify that, for α < x < γ,
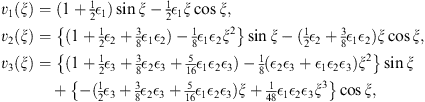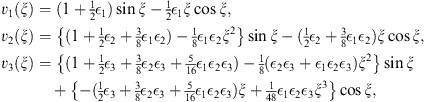
| (A.155) |
etc. These solutions can also be readily derived by directly using the differential equation satisfied by ψn (x) = χ (x)fn (x):
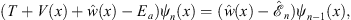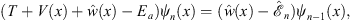
| (A.156) |
where in accordance with (A.14), 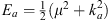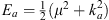 . For α < x < γ, we have
. For α < x < γ, we have
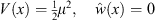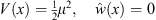
|
and therefore
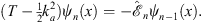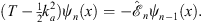
| (A.157) |
Introduce Sn (ξ) and Cn (ξ) to be polynomials in ξ, with
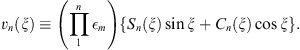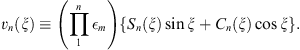
| (A.158) |
From Figs. (A.153), (A.157) and (A.158), we find
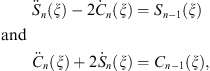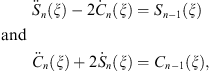
| (A.159) |
where the dot denotes 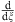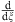 , so that
, so that 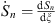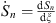 , etc. At x = γ, we have ξ = 0,
, etc. At x = γ, we have ξ = 0, 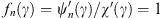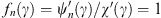 and therefore
and therefore
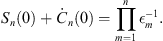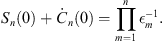
| (A.160) |
For n = 0, S0 (ξ) = 1 and C0 (ξ) = 0. Therefore, for n = 1, (A.159) becomes
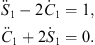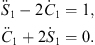
| (A.161) |
Assuming S1 and C1 to be both polynomials of ξ, we can readily verify that S1 is a constant and C1 is proportional to ξ. Using (A.161) and the boundary condition (A.160), we can establish the first equation in (A.155), and likewise the other equations for n > 1.
To understand the structure of v1 (ξ), v2 (ξ), v3 (ξ), … , we may turn to the exact solution ψ (x) given by (A.123). In analogy to (A.153), we define v (ξ) through
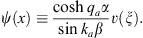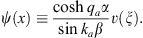
| (A.162) |
Thus, for α < x < γ,

| (A.163) |
From Figs. (A.13), (A.14) and (A.118), we have
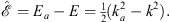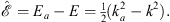
| (A.164) |
In terms of
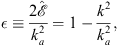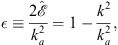
| (A.165) |
we write
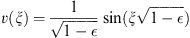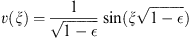
| (A.166) |
with ξ given by (A.151), as before. It is straightforward to expand v (ξ) as a power series in  :
:
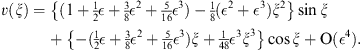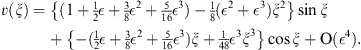
| (A.167) |
To compare the above series with vn (ξ) of (A.155), we can neglect O (  n + 1) in (A.167). The replacements of all linear
n + 1) in (A.167). The replacements of all linear  -terms by
-terms by  n,
n,  2-terms by
2-terms by  n − 1
n − 1  n,
n,  3-terms by
3-terms by  n−2
n−2  n − 1
n − 1  n, etc. lead from (A.167) to vn (ξ). It is of interest to note that the expansion (A.167) of v (ξ) in power of
n, etc. lead from (A.167) to vn (ξ). It is of interest to note that the expansion (A.167) of v (ξ) in power of  has a radius of convergence
has a radius of convergence
|  |<1. |<1.
| (A.168) |
On the other hand, the iterative sequence {vn (ξ)} is always convergent, on account of the Hierarchy Theorem. The main difference between Figs. (A.155) and (A.167) is that in (A.155) each iterative  n is determined by the fraction (A.143).
n is determined by the fraction (A.143).
In a similar way, we can derive ψn (x) in other regions, −α < x < α and −γ < x < −α. The results for n = 1 are given in Table 2. The functions  1 (x) and ξ (x) are discontinuous from region to region. The constants κII and ρII are determined by requiring ψ1 (x) and and
1 (x) and ξ (x) are discontinuous from region to region. The constants κII and ρII are determined by requiring ψ1 (x) and and 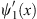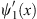 to be continuous at x = α. In region I, when x = α+, we have
to be continuous at x = α. In region I, when x = α+, we have
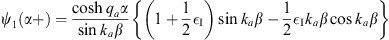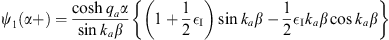
| (A.169) |
and
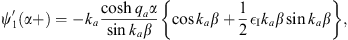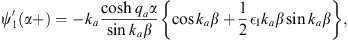
| (A.170) |
where the constant
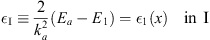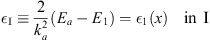
| (A.171) |
with
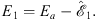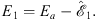
| (A.172) |
In region II, when x = α−
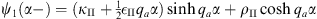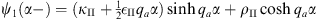
| (A.173) |
and
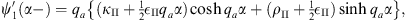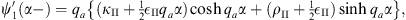
| (A.174) |
where the constant
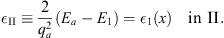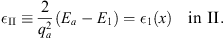
| (A.175) |
The constants κII and ρII are determined by
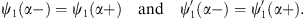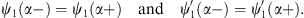
| (A.176) |
Likewise, the constants κIII and ρIII are given by
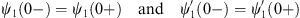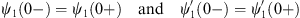
| (A.177) |
and the constants κIV and E1 are determined by

| (A.178) |
 Table 2.
Table 2.
The n = 1 iterative solution ψ1 (x) in the four regions: I (α < x < γ), II (0 < x < α), III (−α < x < 0), and IV (−γ < x < −α)
| Region |  1 (x) 1 (x)
| ξ (x) | ψ1 (x) |
| I | 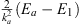
| ka (−x + γ) | 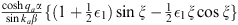
|
| II | 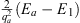
| qax | 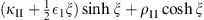
|
| III | 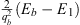
| −qbx | 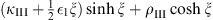
|
| IV | 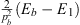
| pb (x + γ) | 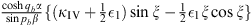
|
The constants 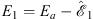 , κII, κIII, κIV, ρII, and ρIII are given by Figs. (A.176), (A.177) and (A.178).
, κII, κIII, κIV, ρII, and ρIII are given by Figs. (A.176), (A.177) and (A.178).
| <== previous lecture | | | next lecture ==> |
| A.2. Square-well example (Cont.) | | | Abstract |