
Introduction
Date: 2015-10-07; view: 686.
Article Outline
1. Introduction
2. The star product formalism
3. Geometric algebra and the Clifford star product
4. Geometric algebra and classical mechanics
5. Non-relativistic quantum mechanics
6. Spacetime algebra and Dirac theory
7. Conclusions
References

Geometric algebra goes back to early ideas of Hamilton, Grassmann, and Clifford. But it was first developed into a full formalism by Hestenes in [1] and [2]. The formalism of geometric algebra is based on the definition of the geometric or Clifford product. This product is for vectors defined as the sum of the scalar and the wedge product and equips the vector space with the algebraic structure of a Clifford algebra. This structure then proved to be a very powerful tool, that allows to describe and generalize the structures of vector analysis, of complex analysis and of the theory of spin in a unified and clear formalism. The formalism can then be used to describe classical mechanics in the realm of geometric algebra instead of linear algebra, which is advantageous in many respects [3] and [4]. It is also possible to generalize the formalism from the algebra of space to the algebra of spacetime in order to describe electrodynamics and special relativity [1] and [4].
In quantum mechanics the Clifford structures of the σ- and the γ-matrices correspond to the structures of geometric algebra. So by formulating classical physics and quantum physics with geometric algebra one achieves a formal unification of both areas on a geometric level. Nevertheless this formulation is conceptually not totally unified, because classical mechanics is still formulated on the phase space while quantum mechanics is formulated in Hilbert space. To achieve a totally unified formulation we will here combine geometric algebra with the star product formalism. The star product formalism [5] appears in the context of deformation quantization where one describes the non-commutativity that enters physics in quantum mechanics not by using non-commuting objects like operators, but by introducing a non-commutative product on the phase space that replaces the conventional product of functions. This star product is so constructed that the quantized star product of two phase space functions corresponds to the operator product of the quantized factors, which then allows to do quantum mechanics on phase space. To include spin in this formalism we used in [6] and [7] fermionic star products that result directly from deformation quantization of pseudoclassical mechanics [8]. Fermionic star products were already discussed in [5], where it was noticed that they lead to a cliffordization of the underlying Grassmann algebra. So it is possible to describe a Clifford algebra as a deformed Grassmann algebra, where this deformation is nothing else than Chevalley cliffordization [7].
In this paper, we will use the fact that geometric algebra can be formulated in terms of a Grassmann algebra [9]. We will show that in this context the geometric product can be made explicit as a fermionic star product. It is then straight forward to translate classical mechanics described with geometric algebra into a version where it is described in terms of fermionic deformed super analysis. The fermionic part of the formalism represents hereby the basis vector structure of the space on which the theory is formulated, i.e., the three-dimensional space, the phase space or the spacetime. In all cases we consider only the case of flat spaces. In a second step one can then go over to quantum mechanics, where we use here deformation quantization, while in [9] canonical and path integral quantization was used. Combining in this way geometric algebra formulated with a fermionic star product with the bosonic star product of deformation quantization one arrives at a supersymmetric star product formalism that allows to describe quantum mechanics with spin in a unified manner. Moreover by using star products one can immediately give the classical 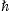 → 0 limit and see how the spin as a physical observable vanishes. Furthermore, one can see that classical mechanics can be described as a half deformed theory, while quantum mechanics is a totally deformed theory, i.e., in classical mechanics the star product acts only on the fermionic basis vector part of the formalism, while for
→ 0 limit and see how the spin as a physical observable vanishes. Furthermore, one can see that classical mechanics can be described as a half deformed theory, while quantum mechanics is a totally deformed theory, i.e., in classical mechanics the star product acts only on the fermionic basis vector part of the formalism, while for 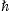 > 0 there exists also a bosonic star product that acts on the coefficients of the basis vectors.
> 0 there exists also a bosonic star product that acts on the coefficients of the basis vectors.
In Section 2 we will very shortly review the bosonic and fermionic star product formalism and show how quantum mechanics with spin can be described in this context. Then we will show how geometric algebra can be formulated with the fermionic star product. We will therefore formulate well-known results of geometric algebra in the formalism of fermionic deformed superanalysis. Afterwards in Sections 5 and 6 we will extend the formalism to the case of non-relativistic quantum mechanics and Dirac theory by using the bosonic Moyal product.
| <== previous lecture | | | next lecture ==> |
| Abstract | | | The star product formalism |